Motzkin number
Encyclopedia
In mathematics
, a Motzkin number for a given number n (named after Theodore Motzkin
) is the number of different ways of drawing non-intersecting chords
on a circle
between n points. The Motzkin numbers have very diverse applications in geometry
, combinatorics
and number theory
. The recurrence relation is:

The first few Motzkin numbers are :
1, 1, 2, 4, 9, 21
, 51, 127
, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019, 142547559, 400763223, 1129760415, 3192727797, 9043402501, 25669818476, 73007772802, 208023278209, 593742784829
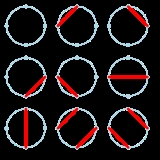
The following figure shows the 9 ways to draw non-intersecting chords between 4 points on a circle.

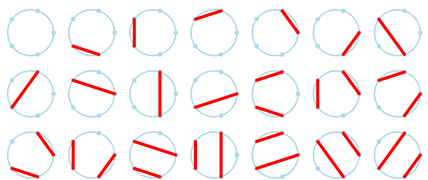
The following figure shows the 21 ways to draw non-intersecting chords between 5 points on a circle.
A Motzkin prime is a Motzkin number that is prime
. As of October 2007, four such primes are known :
2, 127, 15511, 953467954114363
The Motzkin number for n is also the number of positive integer sequences n−1 long in which the opening and ending elements are either 1 or 2, and the difference between any two consecutive elements is −1, 0 or 1.
Also on the upper right quadrant of a grid, the Motzkin number for n gives the number of routes from coordinate (0, 0) to coordinate (n, 0) on n steps if one is allowed to move only to the right (up, down or straight) at each step but forbidden from dipping below the y = 0 axis.
For example, the following figure shows the 9 valid Motzkin paths from (0, 0) to (4, 0):

There are at least fourteen different manifestations of Motzkin numbers in different branches of mathematics, as enumerated by in their survey of Motzkin numbers.
showed that vexillary involutions are enumerated by Motzkin numbers.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Motzkin number for a given number n (named after Theodore Motzkin
Theodore Motzkin
Theodore Samuel Motzkin was an Israeli-American mathematician.- Biography :Motzkin's father, Leo Motzkin, was a noted Russian Zionist leader.Motzkin received his Ph.D...
) is the number of different ways of drawing non-intersecting chords
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
on a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
between n points. The Motzkin numbers have very diverse applications in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. The recurrence relation is:

The first few Motzkin numbers are :
1, 1, 2, 4, 9, 21
21 (number)
21 is the natural number following 20 and preceding 22.-In mathematics:Twenty-one is the fifth discrete Semiprime and the second in the family. With 22 it forms the second discrete Semiprime pair...
, 51, 127
127 (number)
127 is the natural number following 126 and preceding 128.- In mathematics :*As a Mersenne prime, 127 is related to the perfect number 8128. 127 is also an exponent for the Mersenne prime 2127 - 1, making 127 a double Mersenne prime...
, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019, 142547559, 400763223, 1129760415, 3192727797, 9043402501, 25669818476, 73007772802, 208023278209, 593742784829
The following figure shows the 9 ways to draw non-intersecting chords between 4 points on a circle.

The following figure shows the 21 ways to draw non-intersecting chords between 5 points on a circle.

A Motzkin prime is a Motzkin number that is prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. As of October 2007, four such primes are known :
2, 127, 15511, 953467954114363
The Motzkin number for n is also the number of positive integer sequences n−1 long in which the opening and ending elements are either 1 or 2, and the difference between any two consecutive elements is −1, 0 or 1.
Also on the upper right quadrant of a grid, the Motzkin number for n gives the number of routes from coordinate (0, 0) to coordinate (n, 0) on n steps if one is allowed to move only to the right (up, down or straight) at each step but forbidden from dipping below the y = 0 axis.
For example, the following figure shows the 9 valid Motzkin paths from (0, 0) to (4, 0):

There are at least fourteen different manifestations of Motzkin numbers in different branches of mathematics, as enumerated by in their survey of Motzkin numbers.
showed that vexillary involutions are enumerated by Motzkin numbers.

