
Alternating factorial
Encyclopedia
In mathematics
, an alternating factorial is the absolute value
of the alternating sum of the first n factorial
s.
This is the same as their sum, with the odd-indexed factorials multiplied by −1
if n is even, and the even-indexed factorials multiplied by −1 if n is odd, resulting in an alternation of signs of the summands (or alternation of addition and subtraction operators, if preferred). To put it algebraically,
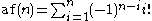
or with the recurrence relation
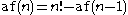
in which af(1) = 1.
The first few alternating factorials are
For example, the third alternating factorial is 1! − 2! + 3!. The fourth alternating factorial is −1! + 2! - 3! + 4! = 19. Regardless of the parity of n, the last (nth) summand, n!, is given a positive sign, the (n - 1)th summand is given a negative sign, and the signs of the lower-indexed summands are alternated accordingly.
This pattern of alternation ensures the resulting sums are all positive integers. Changing the rule so that either the odd- or even-indexed summands are given negative signs (regardless of the parity of n) changes the signs of the resulting sums but not their absolute values.
Miodrag Zivković proved in 1999 that there are only a finite number of alternating factorials that are also prime number
s, since 3612703 divides af(3612702) and therefore divides af(n) for all n ≥ 3612702. , the known primes and probable prime
s are af(n) for
Only the values up to n = 661 have been proved prime in 2006. af(661) is approximately 7.818097272875 × 101578.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an alternating factorial is the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the alternating sum of the first n factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
s.
This is the same as their sum, with the odd-indexed factorials multiplied by −1
-1 (number)
In mathematics, −1 is the additive inverse of 1, that is, the number that when added to 1 gives the additive identity element, 0. It is the negative integer greater than negative two and less than 0....
if n is even, and the even-indexed factorials multiplied by −1 if n is odd, resulting in an alternation of signs of the summands (or alternation of addition and subtraction operators, if preferred). To put it algebraically,
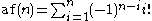
or with the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
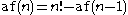
in which af(1) = 1.
The first few alternating factorials are
- 1, 1, 5, 1919 (number)19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90...
, 101101 (number)101 is the natural number following 100 and preceding 102.It is variously pronounced "one hundred and one" / "a hundred and one", "one hundred one" / "a hundred one", and "one oh one"...
, 619, 4421, 35899, 326981, 3301819, 36614981, 442386619, 5784634181, 81393657019
For example, the third alternating factorial is 1! − 2! + 3!. The fourth alternating factorial is −1! + 2! - 3! + 4! = 19. Regardless of the parity of n, the last (nth) summand, n!, is given a positive sign, the (n - 1)th summand is given a negative sign, and the signs of the lower-indexed summands are alternated accordingly.
This pattern of alternation ensures the resulting sums are all positive integers. Changing the rule so that either the odd- or even-indexed summands are given negative signs (regardless of the parity of n) changes the signs of the resulting sums but not their absolute values.
Miodrag Zivković proved in 1999 that there are only a finite number of alternating factorials that are also prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s, since 3612703 divides af(3612702) and therefore divides af(n) for all n ≥ 3612702. , the known primes and probable prime
Probable prime
In number theory, a probable prime is an integer that satisfies a specific condition also satisfied by all prime numbers. Different types of probable primes have different specific conditions...
s are af(n) for
- n = 3, 4, 5, 6, 7, 8, 10, 15, 19, 41, 59, 61, 105, 160, 661, 2653, 3069, 3943, 4053, 4998, 8275, 9158, 11164
Only the values up to n = 661 have been proved prime in 2006. af(661) is approximately 7.818097272875 × 101578.

