Polydivisible number
Encyclopedia
In mathematics
a polydivisible number is a number
with digits
abcde... that has the following properties :
For example, 345654 is a six-digit polydivisible number, but 123456 is not, because 1234 is not a multiple of 4. Polydivisible numbers can be defined in any base
- however, the numbers in this article are all in base 10, so permitted digits are 0 to 9.
The smallest base 10 polydivisible numbers with 1,2,3,4... etc. digits are
1, 10
, 102
, 1020, 10200, 102000, 1020005, 10200056, 102000564, 1020005640
:
The solution to the problem is a nine-digit polydivisible number with the additional condition that it contains the digits 1 to 9 exactly once each. There are 2,492 nine-digit polydivisible numbers, but the only one that satisfies the additional condition is
On average, each polydivisible number with n-1 digits can be extended to a polydivisible number with n digits in 10/n different ways. This leads to the following estimate of the number of n-digit polydivisible numbers, which we will denote by F(n) :

Summing over all values of n, this estimate suggests that the total number of polydivisible numbers will be approximately

In fact, this underestimates the actual number of polydivisible numbers by about 3%.
There are 20,456 polydivisible numbers altogether, and the longest polydivisible number, which has 25 digits, is :
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a polydivisible number is a number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
with digits
Numerical digit
A digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
abcde... that has the following properties :
- Its first digit a is not 0.
- The number formed by its first two digits ab is a multiple of 2.
- The number formed by its first three digits abc is a multiple of 3.
- The number formed by its first four digits abcd is a multiple of 4.
- etc.
For example, 345654 is a six-digit polydivisible number, but 123456 is not, because 1234 is not a multiple of 4. Polydivisible numbers can be defined in any base
Radix
In mathematical numeral systems, the base or radix for the simplest case is the number of unique digits, including zero, that a positional numeral system uses to represent numbers. For example, for the decimal system the radix is ten, because it uses the ten digits from 0 through 9.In any numeral...
- however, the numbers in this article are all in base 10, so permitted digits are 0 to 9.
The smallest base 10 polydivisible numbers with 1,2,3,4... etc. digits are
1, 10
10 (number)
10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 102
102 (number)
102 is the natural number following 101 and preceding 103.-In mathematics:102 is an abundant number and semiperfect number. It is a sphenic number...
, 1020, 10200, 102000, 1020005, 10200056, 102000564, 1020005640
Background
Polydivisible numbers are a generalisation of the following well-known problem in recreational mathematicsRecreational mathematics
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...
:
- Arrange the digits 1 to 9 in order so that the first two digits form a multiple of 2, the first three digits form a multiple of 3, the first four digits form a multiple of 4 etc. and finally the entire number is a multiple of 9.
The solution to the problem is a nine-digit polydivisible number with the additional condition that it contains the digits 1 to 9 exactly once each. There are 2,492 nine-digit polydivisible numbers, but the only one that satisfies the additional condition is
- 381654729
How many polydivisible numbers are there?
If k is a polydivisible number with n-1 digits, then it can be extended to create a polydivisible number with n digits if there is a number between 10k and 10k+9 that is divisible by n. If n is less or equal to 10, then it is always possible to extend an n-1 digit polydivisible number to an n-digit polydivisible number in this way, and indeed there may be more than one possible extension. If n is greater than 10, it is not always possible to extend a polydivisible number in this way, and as n becomes larger, the chances of being able to extend a given polydivisible number become smaller.On average, each polydivisible number with n-1 digits can be extended to a polydivisible number with n digits in 10/n different ways. This leads to the following estimate of the number of n-digit polydivisible numbers, which we will denote by F(n) :

Summing over all values of n, this estimate suggests that the total number of polydivisible numbers will be approximately

In fact, this underestimates the actual number of polydivisible numbers by about 3%.
Counting polydivisible numbers
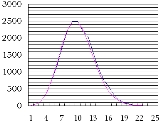
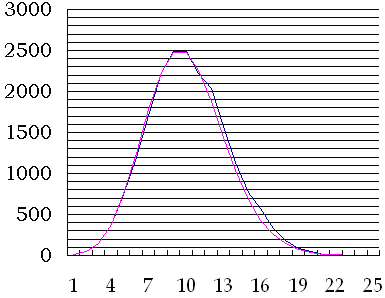
We can find the actual values of F(n) by counting the number of polydivisible numbers with a given length :
| Length n | F(n) | Estimate of F(n) | Length n | F(n) | Estimate of F(n) | Length n | F(n) | Estimate of F(n) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9 | 9 | 11 | 2225 | 2255 | 21 | 18 | 17 | ||
| 2 | 45 | 45 | 12 | 2041 | 1879 | 22 | 12 | 8 | ||
| 3 | 150 | 150 | 13 | 1575 | 1445 | 23 | 6 | 3 | ||
| 4 | 375 | 375 | 14 | 1132 | 1032 | 24 | 3 | 1 | ||
| 5 | 750 | 750 | 15 | 770 | 688 | 25 | 1 | 1 | ||
| 6 | 1200 | 1250 | 16 | 571 | 430 | |||||
| 7 | 1713 | 1786 | 17 | 335 | 253 | |||||
| 8 | 2227 | 2232 | 18 | 180 | 141 | |||||
| 9 | 2492 | 2480 | 19 | 90 | 74 | |||||
| 10 | 2492 | 2480 | 20 | 44 | 37 |
There are 20,456 polydivisible numbers altogether, and the longest polydivisible number, which has 25 digits, is :
- 360 852 885 036 840 078 603 672 5
Related problems
Other problems involving polydivisible numbers include :- Finding polydivisible numbers with additional restrictions on the digits - for example, the longest polydivisible number that only uses even digits is
- 480 006 882 084 660 840 40
- Finding palindromicPalindromic numberA palindromic number or numeral palindrome is a 'symmetrical' number like 16461, that remains the same when its digits are reversed. The term palindromic is derived from palindrome, which refers to a word like rotor that remains unchanged under reversal of its letters...
polydivisible numbers - for example, the longest palindromic polydivisible number is
- 300 006 000 03
- Enumerating polydivisible numbers in other bases.

