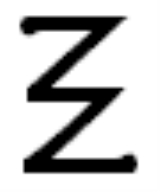
Xi
Encyclopedia
Xi is the 14th letter of the Greek alphabet
. It is pronounced ˈksi in Modern Greek
, and generally ˈzaɪ or ˈsaɪ in English
. In the system of Greek numerals
, it has a value of 60.
Xi is not to be confused with the letter chi
, which gave its form to the Latin letter X
.
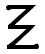Both in classical Ancient Greek
and in Modern Greek
, the letter Ξ represents the sound /ks/. In some archaic local variants
of the Greek alphabet, this letter was missing. Instead, especially in the dialects of most of the Greek mainland and Euboea
, the sound /ks/ was represented by Χ (which in classical Greek is chi
, used for /kʰ/). Because this variant of the Greek alphabet was used in Italy
, the Latin alphabet
borrowed Χ rather than Ξ as the Latin letter X
.
, as the letter ksi .
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
. It is pronounced ˈksi in Modern Greek
Modern Greek
Modern Greek refers to the varieties of the Greek language spoken in the modern era. The beginning of the "modern" period of the language is often symbolically assigned to the fall of the Byzantine Empire in 1453, even though that date marks no clear linguistic boundary and many characteristic...
, and generally ˈzaɪ or ˈsaɪ in English
English language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
. In the system of Greek numerals
Greek numerals
Greek numerals are a system of representing numbers using letters of the Greek alphabet. They are also known by the names Ionian numerals, Milesian numerals , Alexandrian numerals, or alphabetic numerals...
, it has a value of 60.
Xi is not to be confused with the letter chi
Chi (letter)
Chi is the 22nd letter of the Greek alphabet, pronounced as in English.-Greek:-Ancient Greek:Its value in Ancient Greek was an aspirated velar stop .-Koine Greek:...
, which gave its form to the Latin letter X
X
X is the twenty-fourth letter in the basic modern Latin alphabet.-Uses:In mathematics, x is commonly used as the name for an independent variable or unknown value. The usage of x to represent an independent or unknown variable can be traced back to the Arabic word šay شيء = “thing,” used in Arabic...
.
Greek
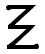
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
and in Modern Greek
Modern Greek
Modern Greek refers to the varieties of the Greek language spoken in the modern era. The beginning of the "modern" period of the language is often symbolically assigned to the fall of the Byzantine Empire in 1453, even though that date marks no clear linguistic boundary and many characteristic...
, the letter Ξ represents the sound /ks/. In some archaic local variants
Archaic Greek alphabets
Many local variants of the Greek alphabet were employed in ancient Greece during the archaic and early classical periods, until they were replaced by the classical 24-letter alphabet that is the standard today, around 400 BC...
of the Greek alphabet, this letter was missing. Instead, especially in the dialects of most of the Greek mainland and Euboea
Euboea
Euboea is the second largest Greek island in area and population, after Crete. The narrow Euripus Strait separates it from Boeotia in mainland Greece. In general outline it is a long and narrow, seahorse-shaped island; it is about long, and varies in breadth from to...
, the sound /ks/ was represented by Χ (which in classical Greek is chi
Chi (letter)
Chi is the 22nd letter of the Greek alphabet, pronounced as in English.-Greek:-Ancient Greek:Its value in Ancient Greek was an aspirated velar stop .-Koine Greek:...
, used for /kʰ/). Because this variant of the Greek alphabet was used in Italy
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
, the Latin alphabet
Latin alphabet
The Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...
borrowed Χ rather than Ξ as the Latin letter X
X
X is the twenty-fourth letter in the basic modern Latin alphabet.-Uses:In mathematics, x is commonly used as the name for an independent variable or unknown value. The usage of x to represent an independent or unknown variable can be traced back to the Arabic word šay شيء = “thing,” used in Arabic...
.
Cyrillic
While having no Latin derivative, the Xi was adopted into the early Cyrillic alphabetEarly Cyrillic alphabet
The Early Cyrillic alphabet is a writing system developed in the First Bulgarian Empire in the 9th or 10th century to write the Old Church Slavonic liturgical language...
, as the letter ksi .
Upper case
The upper-case letter Ξ is used as symbol for:- The "cascade particlesXi (particle)The Xi baryons or cascade particles are a family of subatomic hadron particles which have the symbol and have a +2, +1 or -1 elementary charge or are neutral. They are baryons containing three quarks: one up or down quark, and two heavier quarks...
" in particle physics - Indicating "no change of state" in Z notationZ notationThe Z notation , named after Zermelo–Fraenkel set theory, is a formal specification language used for describing and modelling computing systems. It is targeted at the clear specification of computer programs and computer-based systems in general.-History:...
- The partition functionPartition function (statistical mechanics)Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
under the grand canonical ensembleGrand canonical ensembleIn statistical mechanics, a grand canonical ensemble is a theoretical collection of model systems put together to mirror the calculated probability distribution of microscopic states of a given physical system which is being maintained in a given macroscopic state...
in statistical mechanics - Harish-Chandra's Ξ functionHarish-Chandra's Ξ functionIn mathematical harmonic analysis, Harish-Chandra's Ξ function is a special spherical function on a semisimple Lie group, studied by .Harish-Chandra used it to define Harish-Chandra's Schwartz space....
- The Riemann Xi functionRiemann Xi functionIn mathematics, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation...
Lower case
The lower-case letter ξ is used as a symbol for:- Random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s - Dimensionless distance variable used in the Lane-Emden equationLane-Emden equationIn astrophysics, the Lane–Emden equation is Poisson's equation for the gravitational potential of a self-gravitating, spherically symmetric polytropic fluid. It is named after the astrophysicists Jonathan Homer Lane and Robert Emden...
- Extent of reaction (a topic found most often in chemical engineeringChemical engineeringChemical engineering is the branch of engineering that deals with physical science , and life sciences with mathematics and economics, to the process of converting raw materials or chemicals into more useful or valuable forms...
kinetics) - Eigenvectors
- Damping Ratio C/Ccr(vibrational analysis)
- A parameter in a generalized Pareto distribution
- The symmetric function equation of the Riemann zeta function in mathematicsMathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, also known as the Riemann Xi functionRiemann Xi functionIn mathematics, the Riemann Xi function is a variant of the Riemann zeta function, and is defined so as to have a particularly simple functional equation... - A universal set in the set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
- A number used in the remainder term of Taylor's TheoremTaylor's theoremIn calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
that falls between the limts a and b - A number used in error approximations for formulas that are applications of Taylor's Theorem, such as Newton-Cotes formulasNewton-Cotes formulasIn numerical analysis, the Newton–Cotes formulae, also called the Newton–Cotes quadrature rules or simply Newton–Cotes rules, are a group of formulae for numerical integration based on evaluating the integrand at equally-spaced points...
- One of the two different polypeptide chains of the human embryonic hemoglobinHemoglobinHemoglobin is the iron-containing oxygen-transport metalloprotein in the red blood cells of all vertebrates, with the exception of the fish family Channichthyidae, as well as the tissues of some invertebrates...
types Hb-Portland (ξ2γ2) and Hb-Gower I (ξ2ε2) - The correlation functionCorrelation function (astronomy)In astronomy, a correlation function describes the distribution of galaxies in the universe. By default, correlation function refers to the two-point autocorrelation function. For a given distance, the two-point autocorrelation function is a function of one variable which describes the...
in astronomyAstronomyAstronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth... - Frequency
- A small displacement in MHD plasma stabilityPlasma stabilityAn important field of plasma physics is the stability of the plasma. It usually only makes sense to analyze the stability of a plasma once it has been established that the plasma is in equilibrium. "Equilibrium" asks whether there are net forces that will accelerate any part of the plasma...
theory - A parameter denoted as warped time used to derive the equations for homogeneous azeotropic distillation
- The x-coordinate of computational space as used in Computational Fluid DynamicsComputational fluid dynamicsComputational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
- Potential difference in physics (in volts)
- The radial integral in the spin-orbit matrix operator in atomic physicsAtomic physicsAtomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
. - The Killing vectorKilling vector fieldIn mathematics, a Killing vector field , named after Wilhelm Killing, is a vector field on a Riemannian manifold that preserves the metric. Killing fields are the infinitesimal generators of isometries; that is, flows generated by Killing fields are continuous isometries of the manifold...
in General Relativity. - Average Logarithmic Energy Decrement per Collision (neutron calculations in nuclear physics)