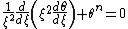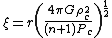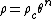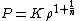In astrophysics

Astrophysics

Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...

, the Lane–Emden equation is Poisson's equation

Poisson's equation

In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...

 for the gravitational potential of a self-gravitating, spherically symmetric polytropic fluid. It is named after the astrophysicists Jonathan Homer Lane

Jonathan Homer Lane

Jonathan Homer Lane was an American astrophysicist and inventor.His education was at the Phillips Academy in Exeter, New Hampshire. He graduated from Yale University in 1846. He worked for the U.S. Patent Office, and became a principal examiner in 1851...

 and Robert Emden

Robert Emden

Jacob Robert Emden was a Swiss astrophysicist and meteorologist. He was born in St. Gallen, Switzerland. In 1907 he became associate professor of physics and meteorology at the Technical University of Munich...

. Its solution provides the run of pressure and density with radius r in terms of a re-scaled radial variable 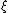and a re-scaled density variable :

where

and

where the subscripts "c" refer to the values of pressure and density at the center of the sphere. Here is the polytropic index in which the pressure and density of the gas are related by the polytropic equation

Note that solutions to the Lane–Emden equation for a given polytropic index are known as polytropes of index . Physically, hydrostatic equilibrium connects the gradient of the potential, the density, and the gradient of the pressure, whereas Poisson's equation connects the potential with the density. It should be clear then if we know nothing about the gas other than the way pressure and density vary with respect to one another, we can reach a solution, in principle. The particular choice of a polytropic gas as given above makes the mathematical statement of the problem particularly succinct, resulting in the Lane–Emden equation. This is a useful "zeroth order" solution for self-gravitating gaseous spheres such as stars. It is still a useful approximation in certain situations, but typically it is a rather limiting assumption.

Solutions of equation

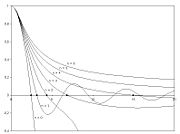
This equation can be solved analytically when n = 0, 1 or 5:

n =	0	1	5
=
=			∞

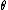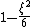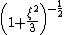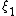Here 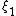is the first root of 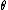, corresponding to the re-scaled radius of the sphere.The equation reduces to a Spherical Bessel differential equation when n = 1 which gives a sinc function.

External links

• Horedt, George Paul ( 1986 ) , Astrophysics and Space Science vol. 126, no. 2, Oct. 1986, p. 357–408. ( ISSN 0004-640X ). Collected at the Smithsonian/NASA Astrophysical Data System.