Newton-Cotes formulas
Encyclopedia
In numerical analysis
, the Newton–Cotes formulae, also called the Newton–Cotes quadrature rules or simply Newton–Cotes rules, are a group of formulae for numerical integration
(also called quadrature) based on evaluating the integrand at equally-spaced points. They are named after Isaac Newton
and Roger Cotes
.
Newton–Cotes formulae can be useful if the value of the integrand at equally-spaced points is given. If it is possible to change the points at which the integrand is evaluated, then other methods such as Gaussian quadrature
and Clenshaw–Curtis quadrature are probably more suitable.
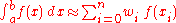
where xi = h i + x0,
with h (called the step size) equal to . The wi are called weights.
As can be seen in the following derivation the weights are derived from the Lagrange basis polynomial
s. This means they depend only on the xi and not on the function ƒ. Let L(x) be the interpolation polynomial in the Lagrange form for the given data points , then
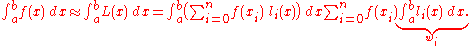
The open Newton–Cotes formula of degree n is stated as
The weights are found in a manner similar to the closed formula.
where the error grows exponentially for large n. Methods such as Gaussian quadrature
and Clenshaw–Curtis quadrature with unequally spaced points (clustered at the endpoints of the integration interval) are stable and much more accurate, and are normally preferred to Newton–Cotes. If these methods can not be used, because the integrand is only given at the fixed equidistributed grid, then Runge's phenomenon can be avoided by using a composite rule, as explained below.
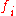is a shorthand for 
, with xi = , and n the degree.
Boole's rule is sometimes mistakenly called Bode's rule due to propagation of a typo in Abramowitz and Stegun, an early reference book.
The exponent of the segment size b − a in the error term shows the rate at which the approximation error decreases. The derivative of ƒ in the error term shows which polynomials can be integrated exactly (i.e., with error equal to zero). Note that the derivative of ƒ in the error term increases by 2 for every other rule. The number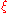
is between a and b.
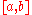must be small itself, which is not true most of the time. For this reason, one usually performs numerical integration by splitting 
into smaller subintervals, applying a Newton–Cotes rule on each subinterval, and adding up the results. This is called a composite rule, see Numerical integration
.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Newton–Cotes formulae, also called the Newton–Cotes quadrature rules or simply Newton–Cotes rules, are a group of formulae for numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
(also called quadrature) based on evaluating the integrand at equally-spaced points. They are named after Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Roger Cotes
Roger Cotes
Roger Cotes FRS was an English mathematician, known for working closely with Isaac Newton by proofreading the second edition of his famous book, the Principia, before publication. He also invented the quadrature formulas known as Newton–Cotes formulas and first introduced what is known today as...
.
Newton–Cotes formulae can be useful if the value of the integrand at equally-spaced points is given. If it is possible to change the points at which the integrand is evaluated, then other methods such as Gaussian quadrature
Gaussian quadrature
In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
and Clenshaw–Curtis quadrature are probably more suitable.
Description
It is assumed that the value of a function ƒ defined on [a, b] is known at equally spaced points xi , for i = 0, …, n, where x0 = a and xn = b. There are two types of Newton–Cotes formulae, the "closed" type which uses the function value at all points, and the "open" type which does not use the function values at the endpoints. The closed Newton-Cotes formula of degree n is stated as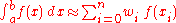where xi = h i + x0,
with h (called the step size) equal to . The wi are called weights.
As can be seen in the following derivation the weights are derived from the Lagrange basis polynomial
Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
s. This means they depend only on the xi and not on the function ƒ. Let L(x) be the interpolation polynomial in the Lagrange form for the given data points , then
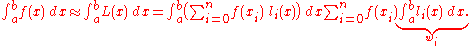
The open Newton–Cotes formula of degree n is stated as
The weights are found in a manner similar to the closed formula.
Instability for high degree
A Newton–Cotes formula of any degree n can be constructed. However, for large n a Newton–Cotes rule can sometimes suffer from catastrophic Runge's phenomenonRunge's phenomenon
In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree...
where the error grows exponentially for large n. Methods such as Gaussian quadrature
Gaussian quadrature
In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
and Clenshaw–Curtis quadrature with unequally spaced points (clustered at the endpoints of the integration interval) are stable and much more accurate, and are normally preferred to Newton–Cotes. If these methods can not be used, because the integrand is only given at the fixed equidistributed grid, then Runge's phenomenon can be avoided by using a composite rule, as explained below.
Closed Newton–Cotes formulae
This table lists some of the Newton–Cotes formulae of the closed type. The notation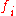 is a shorthand for , with xi = , and n the degree.| Degree | Common name | Formula | Error term |
|---|---|---|---|
| 1 | Trapezoid rule |  |
 |
| 2 | Simpson's rule Simpson's rule In numerical analysis, Simpson's rule is a method for numerical integration, the numerical approximation of definite integrals. Specifically, it is the following approximation:... |
 |
 |
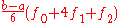| 3 | Simpson's 3/8 rule |  |
 |
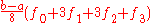| 4 | Boole's rule Boole's rule In mathematics, Boole's rule, named after George Boole, is a method of numerical integration. It approximates an integralby using the values of ƒ at five equally spaced pointsIt is expressed thus Abramowitz and Stegun :... |
 |
 |
Boole's rule is sometimes mistakenly called Bode's rule due to propagation of a typo in Abramowitz and Stegun, an early reference book.
The exponent of the segment size b − a in the error term shows the rate at which the approximation error decreases. The derivative of ƒ in the error term shows which polynomials can be integrated exactly (i.e., with error equal to zero). Note that the derivative of ƒ in the error term increases by 2 for every other rule. The number
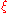is between a and b.Open Newton–Cotes formulae
This table lists some of the Newton–Cotes formulae of the open type. Again, ƒi is a shorthand for ƒ(xi), with xi = , and n the degree.| Degree | Common name | Formula | Error term |
|---|---|---|---|
| 2 | Rectangle rule Rectangle method In mathematics, specifically in integral calculus, the rectangle method computes an approximation to a definite integral, made by finding the area of a collection of rectangles whose heights are determined by the values of the function.Specifically, the interval over which the function is to be... , or midpoint rule |
 |
 |
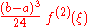| 3 | No name |  |
 |
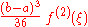| 4 | Milne's rule |  |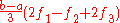
 |
| 5 | No name |  |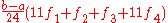
 |
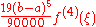Composite rules
For the Newton–Cotes rules to be accurate, the step size h needs to be small, which means that the interval of integration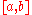 must be small itself, which is not true most of the time. For this reason, one usually performs numerical integration by splitting into smaller subintervals, applying a Newton–Cotes rule on each subinterval, and adding up the results. This is called a composite rule, see Numerical integrationNumerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
.
External links
- Newton–Cotes formulae on www.math-linux.com
- Newton–Cotes Formulae
- Module for Newton–Cotes Integration, fullerton.edu
- Newton–Cotes Integration, numericalmathematics.com
- Newton-Cotes rules with improved stability and noise suppression