
Grand canonical ensemble
Encyclopedia
In statistical mechanics
, a grand canonical ensemble (or macrocanonical ensemble) is a theoretical collection of model systems put together to mirror the calculated probability distribution
of microscopic states of a given physical system which is being maintained in a given macroscopic state. Assuming such a statistical ensemble consists of an overall collection of N microscopic states, the ensemble is constructed so that the proportion pi/N of members of the ensemble which are in microscopic state i is proportional to the probability, over time, of finding the real-world system in that microscopic state i. Thus the ensemble is an imaginary static collection of microscopic states created to mirror the statistics of the successive fluctuations of the macroscopic physical system which is being modeled.
The physical system represented by a grand canonical ensemble is in equilibrium with an external reservoir with respect to both particle and energy exchange. This is an extension of the canonical ensemble
, but instead the grand canonical ensemble being modeled is allowed to exchange energy and particles with its environment. The chemical potential
(or fugacity
) is introduced to specify the fluctuation of the number of particles, just as temperature is introduced into the canonical ensemble to specify the fluctuation of energy.
It is convenient to use the grand canonical ensemble when the number of particles of the system cannot be easily fixed. Especially in quantum systems, e.g., a collection of bosons or fermions, the number of particles is an intrinsic property (rather than an external parameter) of each quantum state. Moreover, fixing the number of particles will cause certain mathematical inconveniences.
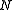
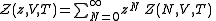
, where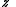 is defined below, and
is defined below, and 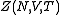 denotes the partition function of the canonical ensemble
denotes the partition function of the canonical ensemble
at temperature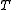 , of volume
, of volume 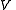 , and with the number of particles fixed at
, and with the number of particles fixed at 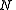 . (In the last step, we have expanded the canonical partition function, and
. (In the last step, we have expanded the canonical partition function, and 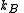 is the Boltzmann constant, the second sum is performed over all microscopic states, denoted by
is the Boltzmann constant, the second sum is performed over all microscopic states, denoted by 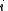 with energy
with energy 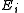 . )
. )
Quantum mechanically, the situation is even simpler (conceptually). For a system of bosons or fermions, it is often mathematically easier to treat the number of particles of the system as an intrinsic property of each quantum (eigen-)state,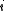 . Therefore the partition function can be written as
. Therefore the partition function can be written as

The parameter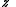 is called fugacity
is called fugacity
, and it represents the ease of adding a new particle into the system. The chemical potential
is directly related to the fugacity through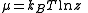 .
.
And the chemical potential is the Gibbs free energy
per particle. (We have used fugacity instead of chemical potential in defining the partition function. This is because fugacity is an independent parameter of partition function to control the number of particles, as temperature to control the energy. On the other hand, the chemical potential itself contains temperature dependence, which may lead to some confusion. )
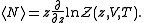
And the average internal energy is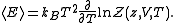
The partition function itself is the product between pressure and volume, divided by
and volume, divided by 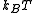 . Such product is nothing but the Gibbs free energy potential related to the grand canonical ensemble
. Such product is nothing but the Gibbs free energy potential related to the grand canonical ensemble
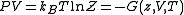
Other thermodynamic potentials
can be obtained through linear combination of above quantities. For example, the Helmholtz free energy (also called
(also called  in some articles, can be obtained as
in some articles, can be obtained as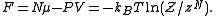
The task of summing over states (calculating the partition function) appears to be simpler if we do not fix the total number of particles of the system because, for a noninteracting system, the partition function of grand canonical ensemble can be converted to a product of the partition functions of individual quantum states. This conversion makes the evaluation much easier. (However this conversion cannot be done in canonical ensemble, where the total number of particles is fixed. )
Each state is a spatial configuration for an individual particle. There may be none or some particles in each state.
In quantum mechanics, all particles are either bosons or fermions. For fermions, no two particles can share a same state. But there is no such constraint for bosons. Therefore the partition function (of grand canonical ensemble) for each state can be written as
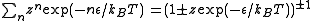
The is the energy of the state. For fermions,
is the energy of the state. For fermions,  can be 0 or 1 (no particle or one particle in the state). For bosons,
can be 0 or 1 (no particle or one particle in the state). For bosons, 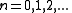 . The upper sign is for fermions and the lower sign is for bosons in the last step. The total partition function is then a product of the ones for individual states.
. The upper sign is for fermions and the lower sign is for bosons in the last step. The total partition function is then a product of the ones for individual states.
. In a suitable representation,
a density matrix ρ takes the form
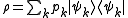
where pk is the probability of a system chosen at random from the ensemble will be in the microstate
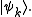
So the trace of ρ, denoted by Tr(ρ), is 1. This is the quantum mechanical analogue of the fact that the accessible region of the classical phase space has total probability 1.
It is also assumed that the ensemble in question is stationary, i.e. it does not change in time. Therefore, by Liouville's theorem
, [ρ, H] = 0, i.e. ρH = Hρ where H is the Hamiltonian
of the system. Thus the density matrix describing ρ is diagonal in the energy representation.
Suppose

where Ei is the energy of the i-th energy eigenstate. If a system i-th energy eigenstate has ni number of particles, the corresponding observable, the number operator, is given by
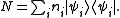
From classical considerations, we know that the state
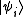
has (unnormalized) probability
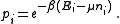
Thus the grand canonical ensemble is the mixed state
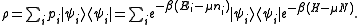
The grand partition, the normalizing constant for Tr(ρ) to be 1, is
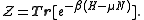
Remember that for the grand partition, the states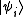 are states with multiple particles in Fock space
are states with multiple particles in Fock space
, and the trace sums over all of them. In the special case of a non-interacting system, the grand partition can be simplified and expressed in terms of the eigenvalues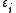 of the single-particle Hamiltonian; after all, the eigenvalues of the multiple-particle Hamiltonian will have the form
of the single-particle Hamiltonian; after all, the eigenvalues of the multiple-particle Hamiltonian will have the form
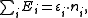
weighting each energy state with the number of particles in that state.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, a grand canonical ensemble (or macrocanonical ensemble) is a theoretical collection of model systems put together to mirror the calculated probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of microscopic states of a given physical system which is being maintained in a given macroscopic state. Assuming such a statistical ensemble consists of an overall collection of N microscopic states, the ensemble is constructed so that the proportion pi/N of members of the ensemble which are in microscopic state i is proportional to the probability, over time, of finding the real-world system in that microscopic state i. Thus the ensemble is an imaginary static collection of microscopic states created to mirror the statistics of the successive fluctuations of the macroscopic physical system which is being modeled.
The physical system represented by a grand canonical ensemble is in equilibrium with an external reservoir with respect to both particle and energy exchange. This is an extension of the canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
, but instead the grand canonical ensemble being modeled is allowed to exchange energy and particles with its environment. The chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
(or fugacity
Fugacity
In chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
) is introduced to specify the fluctuation of the number of particles, just as temperature is introduced into the canonical ensemble to specify the fluctuation of energy.
It is convenient to use the grand canonical ensemble when the number of particles of the system cannot be easily fixed. Especially in quantum systems, e.g., a collection of bosons or fermions, the number of particles is an intrinsic property (rather than an external parameter) of each quantum state. Moreover, fixing the number of particles will cause certain mathematical inconveniences.
The partition function
Classically, the partition function of the grand canonical ensemble is given as a weighted sum of canonical partition functions with different number of particles,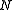
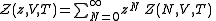
, where
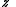 is defined below, and
is defined below, and 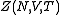 denotes the partition function of the canonical ensemble
denotes the partition function of the canonical ensembleCanonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...
at temperature
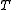 , of volume
, of volume 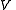 , and with the number of particles fixed at
, and with the number of particles fixed at 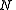 . (In the last step, we have expanded the canonical partition function, and
. (In the last step, we have expanded the canonical partition function, and 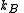 is the Boltzmann constant, the second sum is performed over all microscopic states, denoted by
is the Boltzmann constant, the second sum is performed over all microscopic states, denoted by 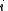 with energy
with energy 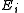 . )
. )Quantum mechanically, the situation is even simpler (conceptually). For a system of bosons or fermions, it is often mathematically easier to treat the number of particles of the system as an intrinsic property of each quantum (eigen-)state,
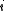 . Therefore the partition function can be written as
. Therefore the partition function can be written as
The parameter
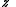 is called fugacity
is called fugacityFugacity
In chemical thermodynamics, the fugacity of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas ...
, and it represents the ease of adding a new particle into the system. The chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
is directly related to the fugacity through
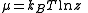 .
.And the chemical potential is the Gibbs free energy
Gibbs free energy
In thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
per particle. (We have used fugacity instead of chemical potential in defining the partition function. This is because fugacity is an independent parameter of partition function to control the number of particles, as temperature to control the energy. On the other hand, the chemical potential itself contains temperature dependence, which may lead to some confusion. )
Thermodynamic quantities
The average number of particles of the ensemble is obtained as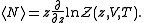
And the average internal energy is
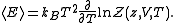
The partition function itself is the product between pressure
 and volume, divided by
and volume, divided by 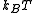 . Such product is nothing but the Gibbs free energy potential related to the grand canonical ensemble
. Such product is nothing but the Gibbs free energy potential related to the grand canonical ensemble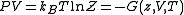
Other thermodynamic potentials
Thermodynamic potentials
A thermodynamic potential is a scalar function used to represent the thermodynamic state of a system. The concept of thermodynamic potentials was introduced by Pierre Duhem in 1886. Josiah Willard Gibbs in his papers used the term fundamental functions. One main thermodynamic potential that has a...
can be obtained through linear combination of above quantities. For example, the Helmholtz free energy
 (also called
(also called  in some articles, can be obtained as
in some articles, can be obtained as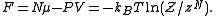
Statistics of bosons and fermions
For a quantum mechanical system, the eigenvalues (energies) and the corresponding eigenvectors (eigenstates) of the Hamiltonian (the energy function) completely describe the system. For a macroscopic system, the number of eigenstates (microscopic states) is enormous. Statistical mechanics provides a way to average all microscopic states to obtain meaningful macroscopic quantities.The task of summing over states (calculating the partition function) appears to be simpler if we do not fix the total number of particles of the system because, for a noninteracting system, the partition function of grand canonical ensemble can be converted to a product of the partition functions of individual quantum states. This conversion makes the evaluation much easier. (However this conversion cannot be done in canonical ensemble, where the total number of particles is fixed. )
Each state is a spatial configuration for an individual particle. There may be none or some particles in each state.
In quantum mechanics, all particles are either bosons or fermions. For fermions, no two particles can share a same state. But there is no such constraint for bosons. Therefore the partition function (of grand canonical ensemble) for each state can be written as
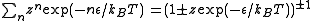
The
 is the energy of the state. For fermions,
is the energy of the state. For fermions,  can be 0 or 1 (no particle or one particle in the state). For bosons,
can be 0 or 1 (no particle or one particle in the state). For bosons, 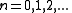 . The upper sign is for fermions and the lower sign is for bosons in the last step. The total partition function is then a product of the ones for individual states.
. The upper sign is for fermions and the lower sign is for bosons in the last step. The total partition function is then a product of the ones for individual states.Quantum mechanical ensemble
An ensemble of quantum mechanical systems is described by a density matrixDensity matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
. In a suitable representation,
a density matrix ρ takes the form
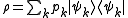
where pk is the probability of a system chosen at random from the ensemble will be in the microstate
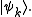
So the trace of ρ, denoted by Tr(ρ), is 1. This is the quantum mechanical analogue of the fact that the accessible region of the classical phase space has total probability 1.
It is also assumed that the ensemble in question is stationary, i.e. it does not change in time. Therefore, by Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
, [ρ, H] = 0, i.e. ρH = Hρ where H is the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of the system. Thus the density matrix describing ρ is diagonal in the energy representation.
Suppose

where Ei is the energy of the i-th energy eigenstate. If a system i-th energy eigenstate has ni number of particles, the corresponding observable, the number operator, is given by
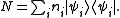
From classical considerations, we know that the state
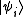
has (unnormalized) probability
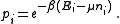
Thus the grand canonical ensemble is the mixed state
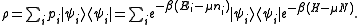
The grand partition, the normalizing constant for Tr(ρ) to be 1, is
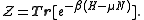
Remember that for the grand partition, the states
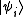 are states with multiple particles in Fock space
are states with multiple particles in Fock spaceFock space
The Fock space is an algebraic system used in quantum mechanics to describe quantum states with a variable or unknown number of particles. It is named after V. A...
, and the trace sums over all of them. In the special case of a non-interacting system, the grand partition can be simplified and expressed in terms of the eigenvalues
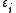 of the single-particle Hamiltonian; after all, the eigenvalues of the multiple-particle Hamiltonian will have the form
of the single-particle Hamiltonian; after all, the eigenvalues of the multiple-particle Hamiltonian will have the form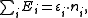
weighting each energy state with the number of particles in that state.

