Weinberg-Witten theorem
Encyclopedia
In theoretical physics
, the Weinberg–Witten theorem (WW), proved by Steven Weinberg
and Edward Witten
, states that massless particles (either composite or elementary) with spin j > 1/2, cannot carry a Lorentz-covariant current, while massless particles with spin j > 1 cannot carry a Lorentz-covariant stress-energy. The theorem is usually interpreted to mean that the graviton (j = 2) cannot be a composite particle in a relativistic quantum field theory
.
theories, technicolor
and the like were very popular and some people speculated that gravity might be an emergent phenomenon or that gluon
s might be composite. Weinberg and Witten, on the other hand, developed a no-go theorem
that excludes, under very general assumptions, the hypothetical composite and emergent theories. Decades later new theories of emergent gravity are proposed and mainstream high-energy physicists are still using this theorem to "debunk
" such theories. Because most of these emergent theories aren't Lorentz covariant, the WW theorem doesn't apply. The violation of Lorentz covariance
, however, usually leads to other problems.
, who did not publish it:
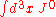. We shall consider the matrix elements of the charge and of the current 
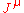for one-particle asymptotic states, of equal helicity, 
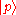and 
, labeled by their lightlike 4-momenta. We shall consider the case in which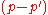 
isn't null, which means that the momentum transfer is spacelike. Let q be the eigenvalue of those states for the charge operator Q, so that:
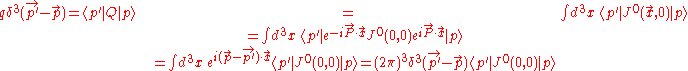
where we have now made used of translational covariance, which is part of the Poincaré covariance. Thus:
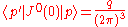
with
.
Let's transform to a reference frame
where p moves along the positive z-axis and p′ moves along the negative z-axis. This is always possible for any spacelike momentum transfer.
In this reference frame,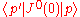
and 
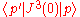change by the phase factor 
under rotation
s by θ counterclockwise about the z-axis whereas
and 
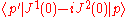change by the phase factors 
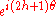and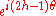 
respectively.
If h is nonzero, we need to specify the phases of states. In general, this can't be done in a Lorentz-invariant way (see Thomas precession
), but the one particle Hilbert space is Lorentz-covariant. So, if we make any arbitrary but fixed choice for the phases, then each of the matrix components in the previous paragraph has to be invariant under the rotations about the z-axis. So, unless |h| = 0 or 1/2, all of the components have to be zero.
Weinberg and Witten did not assume the continuity
.
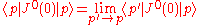Rather, the authors argue that the physical (i.e., the measurable) quantum numbers of a massless particle are always defined by the matrix elements in the limit of zero momentum, defined for a sequence of spacelike momentum transfers. Also,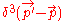
in the first equation can be replaced by "smeared out" Dirac delta function
, which corresponds to performing the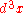
volume integral over a finite box.
The proof of the second part of theorem is completely analogous, replacing the matrix elements of the current with the matrix elements of the stress-energy tensor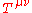
:
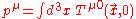and
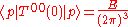
with
.
For spacelike momentum transfers, we can go to the reference frame where p′ + p is along the t-axis and p′ − p is along the z-axis. In this reference frame, the components of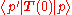
transforms as 
, 
,
, 
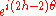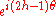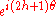or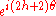 
under a rotation by θ about the z-axis. Similarly, we can conclude that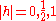 
Note that this theorem also applies to free field
theories. If they contain massless particles with the "wrong" helicity/charge, they have to be gauge theories.
If let's say gravity is an emergent theory of a fundamentally flat theory over a flat Minkowski spacetime, then by Noether's theorem
, we have a conserved stress-energy tensor which is Poincaré covariant. If the theory has an internal gauge symmetry (of the Yang-Mills kind), we may pick the Belinfante-Rosenfeld stress-energy tensor which is gauge-invariant. As there is no fundamental diffeomorphism
symmetry, we don't have to worry about that this tensor isn't BRST-closed under diffeomorphisms. So, the Weinberg–Witten theorem applies and we can't get a massless spin-2 (i.e. helicity ±2) composite
/emergent graviton
.
If let's say we have a theory with a fundamental conserved 4-current associated with a global symmetry
, then we can't have emergent/composite massless spin-1 particles which are charged under that global symmetry.
cohomology, i.e. a quotient space
, it is really an equivalence class of states. As such,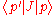
is only well defined if J is BRST-closed. But if J isn't gauge-invariant, then J isn't BRST-closed in general. The current defined as 
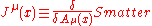is not conserved because it satisfies 
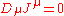instead of 
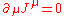where D is the covariant derivative
. The current defined after a gauge-fixing like the Coulomb gauge is conserved but isn't Lorentz covariant.
s associated with spontaneously broken symmetries are massive. For example, in QCD
, we have electrically charged rho meson
s which can be described by an emergent hidden gauge symmetry which is spontaneously broken. Therefore, there is nothing in principle stopping us from having composite preon models of W and Z bosons.
On a similar note, even though the photon
is charged under the SU(2) weak symmetry (because it is the gauge boson
associated with a linear combination of weak isospin and hypercharge), it is also moving through a condensate of such charges, and so, isn't an exact eigenstate of the weak charges and this theorem doesn't apply either.
Massive gravity
On a similar note, it is possible to have a composite/emergent theory of massive gravity
.
General relativity
In GR, we have diffeomorphisms and A|ψ> (over an element |ψ> of the BRST cohomology) only makes sense if A is BRST-closed. There are no local BRST-closed operators and this includes any stress-energy tensor that we can think of.
Induced gravity
In induced gravity, the fundamental theory is also diffeomorphism invariant and the same comment applies.
Seiberg duality
If we take N=1 chiral
super
QCD
with Nc colors and Nf flavors with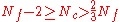
, then by the Seiberg duality
, this theory is dual to a nonabelian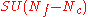
gauge theory which is trivial (i.e. free) in the infrared
limit. As such, the dual theory doesn't suffer from any infraparticle problem or a continuous mass spectrum. Despite this, the dual theory is still a nonabelian Yang-Mills theory. Because of this, the dual magnetic current still suffers from all the same problems even though it is an "emergent current". Free theories aren't exempt from the Weinberg–Witten theorem.
Conformal field theory
In a conformal field theory, the only truly massless particles are noninteracting singleton
s (see singleton field
). The other "particles"/bound states have a continuous mass spectrum
which can take on any arbitrarily small nonzero mass. So, we can have spin-3/2 and spin-2 bound states with arbitrarily small masses but still not violate the theorem. In other words, they are infraparticle
s.
Infraparticle
Two otherwise identical charged infraparticles moving with different velocities belong to different superselection sector
s. Let's say they have momenta p′ and p respectively. Then as Jμ(0) is a local neutral operator
, it does not map between different superselection sectors. So,
is zero. The only way |p′'> and |p> can belong in the same sector is if they have the same velocity, which means that they are proportional to each other, i.e. a null or zero momentum transfer, which isn't covered in the proof. So, infraparticles violate the continuity assumption
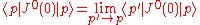
This doesn't mean of course that the momentum of a charge particle can't change by some spacelike momentum. It only means that if the incoming state is a one infraparticle state, then the outgoing state contains an infraparticle together with a number of soft quanta. This is nothing other than the inevitable bremsstrahlung
. But this also means that the outgoing state isn't a one particle state.
Acoustic metric
These theories are not Lorentz covariant. However, some of these theories can give rise to an approximate emergent Lorentz symmetry at low energies so that we can both have the cake and eat it too.
Superstring theory
Superstring theory defined over a background metric (possibly with some fluxes) over a 10D space which is the product of a flat 4D Minkowski space and a compact 6D space has a massless graviton in its spectrum. This is an emergent particle coming from the vibrations of a superstring. Let's look at how we would go about defining the stress-energy tensor. The background is given by g (the metric) and a couple of other fields. The effective action
is a functional of the background. The VEV of the stress-energy tensor is then defined as the functional derivative
The stress-energy operator is defined as a vertex operator corresponding to this infinitesimal change in the background metric.
Not all backgrounds are permissible. Superstrings have to have superconformal symmetry, which is a super generalization of Weyl symmetry, in order to be consistent but they are only superconformal when propagating over some special backgrounds (which satisfy the Einstein field equations plus some higher order corrections). Because of this, the effective action is only defined over these special backgrounds and the functional derivative is not well-defined. The vertex operator for the stress-energy tensor at a point also doesn't exist.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Weinberg–Witten theorem (WW), proved by Steven Weinberg
Steven Weinberg
Steven Weinberg is an American theoretical physicist and Nobel laureate in Physics for his contributions with Abdus Salam and Sheldon Glashow to the unification of the weak force and electromagnetic interaction between elementary particles....
and Edward Witten
Edward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
, states that massless particles (either composite or elementary) with spin j > 1/2, cannot carry a Lorentz-covariant current, while massless particles with spin j > 1 cannot carry a Lorentz-covariant stress-energy. The theorem is usually interpreted to mean that the graviton (j = 2) cannot be a composite particle in a relativistic quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Background
During the 1980's, preonPreon
In particle physics, preons are postulated "point-like" particles, conceived to be subcomponents of quarks and leptons. The word was coined by Jogesh Pati and Abdus Salam in 1974...
theories, technicolor
Technicolor (physics)
Technicolor theories are models of physics beyond the standard model that address electroweak symmetry breaking, the mechanism through which elementary particles acquire masses...
and the like were very popular and some people speculated that gravity might be an emergent phenomenon or that gluon
Gluon
Gluons are elementary particles which act as the exchange particles for the color force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles....
s might be composite. Weinberg and Witten, on the other hand, developed a no-go theorem
No-go theorem
In theoretical physics, a no-go theorem is a theorem that states that a particular situation is not physically possible.-Examples of no-go theorems:* Bell's theorem* Coleman–Mandula theorem* Haag-Lopuszanski-Sohnius theorem* Earnshaw's theorem...
that excludes, under very general assumptions, the hypothetical composite and emergent theories. Decades later new theories of emergent gravity are proposed and mainstream high-energy physicists are still using this theorem to "debunk
Debunker
A debunker is an individual who attempts to discredit and contradict claims as being false, exaggerated or pretentious. The term is closely associated with skeptical investigation of, or in some cases irrational resistance to, controversial topics such as U.F.O.s, claimed paranormal phenomena,...
" such theories. Because most of these emergent theories aren't Lorentz covariant, the WW theorem doesn't apply. The violation of Lorentz covariance
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
, however, usually leads to other problems.
Theorem
Weinberg and Witten proved two separate results. According to them, the first is due to Sidney ColemanSidney Coleman
Sidney Richard Coleman was an American theoretical physicist who studied under Murray Gell-Mann.- Life and work :Sidney Coleman grew up on the Far North Side of Chicago...
, who did not publish it:
- A 3 + 1D QFT (quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
) with a conservedConserved currentIn physics a conserved current is a current, j^\mu, that satisfies the continuity equation \partial_\mu j^\mu=0. The continuity equation represents a conservation law, hence the name....
4-vector current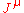
(see four-currentFour-currentIn special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
) which is Poincaré covariant (and gauge invariant if there happens to be any gauge symmetry which hasn't been gauge-fixed) does not admit massless particles with helicityHelicityThe term helicity has several meanings. In physics, all referring to a phenomenon that resembles a helix. See:*helicity , the extent to which corkscrew-like motion occurs...
|h| > 1/2 that also have nonzero charges associated with the conserved current in question.
- A 3 + 1D QFT with a conserved stress-energy tensorStress-energy tensorThe stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
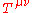which is Poincaré covariant (and gauge invariant if there happens to be any gauge symmetry which hasn't been gauge-fixed) does not admit massless particles with helicity |h| > 1.
A sketch of the proof
The conserved charge Q is given by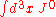. We shall consider the matrix elements of the charge and of the current 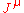for one-particle asymptotic states, of equal helicity, 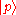and , labeled by their lightlike 4-momenta. We shall consider the case in which 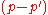isn't null, which means that the momentum transfer is spacelike. Let q be the eigenvalue of those states for the charge operator Q, so that: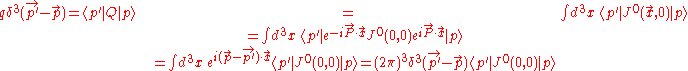where we have now made used of translational covariance, which is part of the Poincaré covariance. Thus:
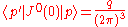
with
.Let's transform to a reference frame
Reference frame
Reference frame may refer to:*Frame of reference, in physics*Reference frame , frames of a compressed video that are used to define future frames...
where p moves along the positive z-axis and p′ moves along the negative z-axis. This is always possible for any spacelike momentum transfer.
In this reference frame,
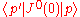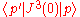and change by the phase factor under rotationRotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
s by θ counterclockwise about the z-axis whereas
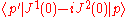and change by the phase factors 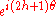and 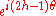respectively.If h is nonzero, we need to specify the phases of states. In general, this can't be done in a Lorentz-invariant way (see Thomas precession
Thomas precession
In physics the Thomas precession, named after Llewellyn Thomas, is a special relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope and relates the angular velocity of the spin of a particle following a curvilinear orbit to the angular...
), but the one particle Hilbert space is Lorentz-covariant. So, if we make any arbitrary but fixed choice for the phases, then each of the matrix components in the previous paragraph has to be invariant under the rotations about the z-axis. So, unless |h| = 0 or 1/2, all of the components have to be zero.
Weinberg and Witten did not assume the continuity
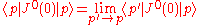.Rather, the authors argue that the physical (i.e., the measurable) quantum numbers of a massless particle are always defined by the matrix elements in the limit of zero momentum, defined for a sequence of spacelike momentum transfers. Also,
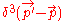in the first equation can be replaced by "smeared out" Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
, which corresponds to performing the
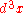volume integral over a finite box.The proof of the second part of theorem is completely analogous, replacing the matrix elements of the current with the matrix elements of the stress-energy tensor
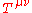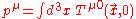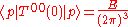
: andwith
.For spacelike momentum transfers, we can go to the reference frame where p′ + p is along the t-axis and p′ − p is along the z-axis. In this reference frame, the components of
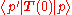transforms as 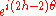, ,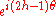, 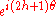or 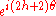under a rotation by θ about the z-axis. Similarly, we can conclude that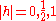 Note that this theorem also applies to free field
Free field
In classical physics, a free field is a field whose equations of motion are given by linear partial differential equations. Such linear PDE's have a unique solution for a given initial condition....
theories. If they contain massless particles with the "wrong" helicity/charge, they have to be gauge theories.
Ruling out emergent theories
What has this theorem got to do with emergence/composite theories?If let's say gravity is an emergent theory of a fundamentally flat theory over a flat Minkowski spacetime, then by Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, we have a conserved stress-energy tensor which is Poincaré covariant. If the theory has an internal gauge symmetry (of the Yang-Mills kind), we may pick the Belinfante-Rosenfeld stress-energy tensor which is gauge-invariant. As there is no fundamental diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
symmetry, we don't have to worry about that this tensor isn't BRST-closed under diffeomorphisms. So, the Weinberg–Witten theorem applies and we can't get a massless spin-2 (i.e. helicity ±2) composite
Composite gravity
In theoretical physics, composite gravity refers to models that attempted to derive general relativity in a framework where the graviton is constructed as a composite bound state of more elementary particles, usually fermions.A theorem by Steven Weinberg and Edward Witten shows that this is not...
/emergent graviton
Graviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
.
If let's say we have a theory with a fundamental conserved 4-current associated with a global symmetry
Global symmetry
A global symmetry is a symmetry that holds at all points in the spacetime under consideration, as opposed to a local symmetry which varies from point to point.Global symmetries require conservation laws, but not forces, in physics.-See also:...
, then we can't have emergent/composite massless spin-1 particles which are charged under that global symmetry.
Nonabelian gauge theories
There are a number of ways to see why nonabelian Yang-Mills theories in the Coulomb phase don't violate this theorem. Yang-Mills theories don't have any conserved 4-current associated with the Yang-Mills charges that are both Poincaré covariant and gauge invariant. Noether's theorem gives a current which is conserved and Poincaré covariant, but not gauge invariant. As |p> is really an element of the BRSTBRST
BRST may refer to:* BRST formalism and quantization in Yang-Mills theories* Big Red Switch Time , computer jargon for switching your computer off, when all other options for a more elegant shutdown have been exhausted...
cohomology, i.e. a quotient space
Quotient space
In topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
, it is really an equivalence class of states. As such,
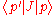is only well defined if J is BRST-closed. But if J isn't gauge-invariant, then J isn't BRST-closed in general. The current defined as 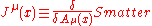is not conserved because it satisfies 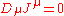instead of 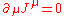where D is the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
. The current defined after a gauge-fixing like the Coulomb gauge is conserved but isn't Lorentz covariant.
Spontaneously broken gauge theories
The gauge bosonGauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s associated with spontaneously broken symmetries are massive. For example, in QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
, we have electrically charged rho meson
Rho meson
In particle physics, a rho meson is a short-lived hadronic particle that is an isospin triplet whose three states are denoted as , and . After the pions and kaons, the rho mesons are the lightest strongly interacting particle with a mass of roughly for all three states...
s which can be described by an emergent hidden gauge symmetry which is spontaneously broken. Therefore, there is nothing in principle stopping us from having composite preon models of W and Z bosons.
On a similar note, even though the photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
is charged under the SU(2) weak symmetry (because it is the gauge boson
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
associated with a linear combination of weak isospin and hypercharge), it is also moving through a condensate of such charges, and so, isn't an exact eigenstate of the weak charges and this theorem doesn't apply either.
Massive gravityMassive gravityIn theoretical physics, massive gravity is a particular generalization of general relativity studied by Hendrik van Dam, Martinus J. G. Veltman , and Vladimir E...
On a similar note, it is possible to have a composite/emergent theory of massive gravityMassive gravity
In theoretical physics, massive gravity is a particular generalization of general relativity studied by Hendrik van Dam, Martinus J. G. Veltman , and Vladimir E...
.
General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
In GR, we have diffeomorphisms and A|ψ> (over an element |ψ> of the BRST cohomology) only makes sense if A is BRST-closed. There are no local BRST-closed operators and this includes any stress-energy tensor that we can think of. Induced gravityInduced gravityInduced gravity is an idea in quantum gravity that space-time background emerges asa mean field approximation of underlying microscopic degrees of freedom, similar to the fluid mechanics approximation of Bose–Einstein condensates...
In induced gravity, the fundamental theory is also diffeomorphism invariant and the same comment applies. Seiberg dualitySeiberg dualityIn quantum field theory, Seiberg duality, conjectured by Nathan Seiberg, is an S-duality relating two different supersymmetric QCDs. The two theories are not identical, but they agree at low energies. More precisely under a renormalization group flow they flow to the same IR fixed point, and so...
If we take N=1 chiralChiral symmetry
In quantum field theory, chiral symmetry is a possible symmetry of the Lagrangian under which the left-handed and right-handed parts of Dirac fields transform independently...
super
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
QCD
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
with Nc colors and Nf flavors with
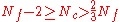, then by the Seiberg dualitySeiberg duality
In quantum field theory, Seiberg duality, conjectured by Nathan Seiberg, is an S-duality relating two different supersymmetric QCDs. The two theories are not identical, but they agree at low energies. More precisely under a renormalization group flow they flow to the same IR fixed point, and so...
, this theory is dual to a nonabelian
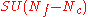gauge theory which is trivial (i.e. free) in the infraredInfrared
Infrared light is electromagnetic radiation with a wavelength longer than that of visible light, measured from the nominal edge of visible red light at 0.74 micrometres , and extending conventionally to 300 µm...
limit. As such, the dual theory doesn't suffer from any infraparticle problem or a continuous mass spectrum. Despite this, the dual theory is still a nonabelian Yang-Mills theory. Because of this, the dual magnetic current still suffers from all the same problems even though it is an "emergent current". Free theories aren't exempt from the Weinberg–Witten theorem.
Conformal field theoryConformal field theoryA conformal field theory is a quantum field theory that is invariant under conformal transformations...
In a conformal field theory, the only truly massless particles are noninteracting singletonSingleton
Singleton may refer to* Singleton , a set with exactly one element* Singleton , a single decision-maker at the highest level of the world order...
s (see singleton field
Singleton field
It is the field of singletons which are the most fundamental unitary and irreducible representation of the Anti de Sitter group SO. They are discovered by Paul Dirac....
). The other "particles"/bound states have a continuous mass spectrum
Mass spectrum
A mass spectrum is an intensity vs. m/z plot representing a chemical analysis. Hence, the mass spectrum of a sample is a pattern representing the distribution of ions by mass in a sample. It is a histogram usually acquired using an instrument called a mass spectrometer...
which can take on any arbitrarily small nonzero mass. So, we can have spin-3/2 and spin-2 bound states with arbitrarily small masses but still not violate the theorem. In other words, they are infraparticle
Infraparticle
An infraparticle is an electrically charged particle and its surrounding cloud of soft photons—of which there are infinite number, by virtue of the infrared divergence of quantum electrodynamics. That is, it is a dressed particle rather than a bare particle...
s.
InfraparticleInfraparticleAn infraparticle is an electrically charged particle and its surrounding cloud of soft photons—of which there are infinite number, by virtue of the infrared divergence of quantum electrodynamics. That is, it is a dressed particle rather than a bare particle...
s
Two otherwise identical charged infraparticles moving with different velocities belong to different superselection sectorSuperselection sector
In Quantum mechanics, superselection extends the concept of selection rules.Superselection rules are postulated rules forbidding the preparation of quantum states that exhibit coherence between eigenstates of certain observables....
s. Let's say they have momenta p′ and p respectively. Then as Jμ(0) is a local neutral operator
Operator
In basic mathematics, an operator is a symbol or function representing a mathematical operation.In terms of vector spaces, an operator is a mapping from one vector space or module to another. Operators are of critical importance to both linear algebra and functional analysis, and they find...
, it does not map between different superselection sectors. So,
is zero. The only way |p′'> and |p> can belong in the same sector is if they have the same velocity, which means that they are proportional to each other, i.e. a null or zero momentum transfer, which isn't covered in the proof. So, infraparticles violate the continuity assumption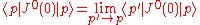This doesn't mean of course that the momentum of a charge particle can't change by some spacelike momentum. It only means that if the incoming state is a one infraparticle state, then the outgoing state contains an infraparticle together with a number of soft quanta. This is nothing other than the inevitable bremsstrahlung
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
. But this also means that the outgoing state isn't a one particle state.
Theories with nonlocal charges
Obviously, a nonlocal charge does not have a local 4-current and a theory with a nonlocal 4-momentum does not have a local stress-energy tensor. Acoustic metricAcoustic metricIn mathematical physics, a metric describes the arrangement of relative distances within a surface or volume, usually measured by signals passing through the region – essentially describing the intrinsic geometry of the region. An acoustic metric will describe the signal-carrying properties...
theories and analog model of gravity
These theories are not Lorentz covariant. However, some of these theories can give rise to an approximate emergent Lorentz symmetry at low energies so that we can both have the cake and eat it too. Superstring theorySuperstring theorySuperstring theory is an attempt to explain all of the particles and fundamental forces of nature in one theory by modelling them as vibrations of tiny supersymmetric strings...
Superstring theory defined over a background metric (possibly with some fluxes) over a 10D space which is the product of a flat 4D Minkowski space and a compact 6D space has a massless graviton in its spectrum. This is an emergent particle coming from the vibrations of a superstring. Let's look at how we would go about defining the stress-energy tensor. The background is given by g (the metric) and a couple of other fields. The effective actionEffective action
In quantum field theory, the effective action is a modified expression for the action, which takes into account quantum-mechanical corrections, in the following sense:...
is a functional of the background. The VEV of the stress-energy tensor is then defined as the functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
The stress-energy operator is defined as a vertex operator corresponding to this infinitesimal change in the background metric.
Not all backgrounds are permissible. Superstrings have to have superconformal symmetry, which is a super generalization of Weyl symmetry, in order to be consistent but they are only superconformal when propagating over some special backgrounds (which satisfy the Einstein field equations plus some higher order corrections). Because of this, the effective action is only defined over these special backgrounds and the functional derivative is not well-defined. The vertex operator for the stress-energy tensor at a point also doesn't exist.