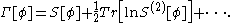Effective action
Encyclopedia
In quantum field theory
, the effective action is a modified expression for the action
, which takes into account quantum-mechanical corrections, in the following sense:
In classical mechanics
, the equations of motion can be derived from the action
by the principle of stationary action. This is not the case in quantum mechanics
, where the amplitudes of all possible motions are added up in a path integral
. However, if the action is replaced by the effective action, the equations of motion for the vacuum expectation values
of the field
s can be derived from the requirement that the effective action be stationary. For example, a field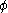
with a potential
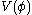, at a low temperature, will not settle in a local minimum of 
, but in a local minimum of the effective potential which can be read off from the effective action.
Furthermore, the effective action can be used instead of the action in the calculation of correlation function
s, and then only tree diagrams
should be taken into account.
. However, the signs and factors of i are different in that case.
Given the partition function
Z[J] in terms of the source field J, the energy functional is its logarithm.
Some physicists use W instead where W = −E. See sign convention
s
In statistical mechanics,
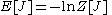
Just as Z is interpreted as the generating functional (aka characteristic function
(al)/moment-generating function
(al) of the probability distribution function
(al) e−S[φ]/Z) of the time ordered VEVs/Schwinger function
(aka moments
) (see path integral formulation
), E (a.k.a. the second characteristic function(al)/cumulant-generating function(al)) is the generator of "connected" time ordered VEVs/connected Schwinger functions (i.e. the cumulant
s) where connected here is interpreted in the sense of the cluster decomposition theorem
which means that these functions approach zero at large spacelike separations, or in approximations using Feynman diagram
s, connected components
of the graph.
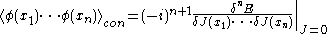
or
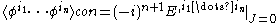
in the deWitt notation
Then the n-point correlation function is the sum over all the possible partitions of the fields involved in the product into products of connected correlation functions. To clarify with an example,
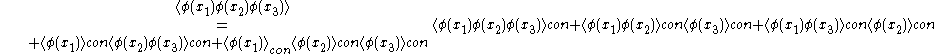
Assuming E is a convex functional
(which is debatable), the Legendre transformation
gives a one-to-one correspondence between the configuration space
of all source fields and its dual vector space, the configuration space of all φ fields. If E is not convex, we take the Fenchel conjugate instead. φ here is a classical field and not a quantum field operator.
Slightly out of the usual sign convention
s for Legendre transforms, the value
or
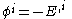
is associated to J. This agrees with the time ordered VEV <φ>J. The Legendre transform of E is the effective action (this corresponds to the rate function
, which is the Fenchel conjugate of the cumulant-generating function, a common construction in statistics
; e.g. the Chernoff bound
)
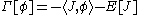
or
where
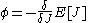
and
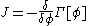
or
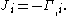
There are some caveats, though, the major one being we don't have a true one-to-one correspondence between the dual configuration spaces.
Let us first consider the case without tadpoles
, i.e.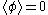
for J=0. In that case, Γ[0] gives the zero-point energy, the first functional derivative
of Γ at φ=0 is zero, the second functional derivative gives the inverse of the full propagator, and the nth functional derivative for n ≥ 3 gives the one particle irreducible correlation functions or 1PI correlation functions. The Dyson equation relates the full propagator, the bare propagator and the 1PI self-energy. The n-point connected functions are given as the sum over all trees with n ≥ 3 1PI's as nodes and full propagators as edges.
But what if we have tadpoles? We can always adjust the source J so that there are no tadpoles, i.e.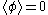
. This corresponds to adding a Feynman rule corresponding to a coupling to the source. For any Feynman diagram, a subtadpole is a subgraph corresponding to a component not connected to any of the external legs which arises after cutting of an edge. Any Feynman diagram with a subtadpole can be evaluated as nonzero, but we can group these diagrams into equivalence classes (two connected diagrams are equivalent if they only vary in their subtadpoles). Therefore, we only need to consider the sum of all connected graphs without subtadpoles. The sum over all graphs in an equivalence class with subtadpoles is zero, since J is adjusted so that 
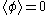. Any graph without subtadpoles do not contain any couplings to the source. A Taylor expansion of the effective action about φ = 0 gives the 1PI's corresponding to these value of the source according to the rules of the previous paragraph. So, we compute the 1PI's to get the Taylor series about 
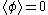. Then, from the effective action that we get from the Taylor series, we find the value of φ which minimizes the effective action. This gives us the VEV of φ when J = 0. Then, we now perform a Taylor series expansion about this VEV after shifting the field φ to a new field redefinition 
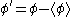(this is the background field method
). Now we can compute the n-point correlations about the J = 0 vacuum.
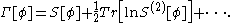
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the effective action is a modified expression for the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
, which takes into account quantum-mechanical corrections, in the following sense:
In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the equations of motion can be derived from the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
by the principle of stationary action. This is not the case in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, where the amplitudes of all possible motions are added up in a path integral
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
. However, if the action is replaced by the effective action, the equations of motion for the vacuum expectation values
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of the field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
s can be derived from the requirement that the effective action be stationary. For example, a field
with a potentialPotential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
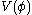, at a low temperature, will not settle in a local minimum of , but in a local minimum of the effective potential which can be read off from the effective action.Furthermore, the effective action can be used instead of the action in the calculation of correlation function
Correlation function (quantum field theory)
In quantum field theory, the matrix element computed by inserting a product of operators between two states, usually the vacuum states, is called a correlation function....
s, and then only tree diagrams
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
should be taken into account.
Mathematical details
Everything in the following article also applies to statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. However, the signs and factors of i are different in that case.
Given the partition function
Partition function (quantum field theory)
In quantum field theory, we have a generating functional, Z[J] of correlation functions and this value, called the partition function is usually expressed by something like the following functional integral:...
Z[J] in terms of the source field J, the energy functional is its logarithm.
Some physicists use W instead where W = −E. See sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
s
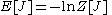
Just as Z is interpreted as the generating functional (aka characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
(al)/moment-generating function
Moment-generating function
In probability theory and statistics, the moment-generating function of any random variable is an alternative definition of its probability distribution. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or...
(al) of the probability distribution function
Probability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
(al) e−S[φ]/Z) of the time ordered VEVs/Schwinger function
Schwinger function
In quantum field theory, the Wightman distributions can be analytically continued to analytic functions in Euclidean space with the domain restricted to the ordered set of points in Euclidean space with no coinciding points...
(aka moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
) (see path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
), E (a.k.a. the second characteristic function(al)/cumulant-generating function(al)) is the generator of "connected" time ordered VEVs/connected Schwinger functions (i.e. the cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s) where connected here is interpreted in the sense of the cluster decomposition theorem
Cluster decomposition theorem
In physics, the cluster decomposition theorem guarantees locality in quantum field theory. According to this theorem, the vacuum expectation value of a product of many operators - each of them being either in region A or in region B where A and B are very separated - asymptotically equals the...
which means that these functions approach zero at large spacelike separations, or in approximations using Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s, connected components
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
of the graph.
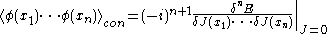
or
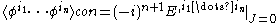
in the deWitt notation
Then the n-point correlation function is the sum over all the possible partitions of the fields involved in the product into products of connected correlation functions. To clarify with an example,
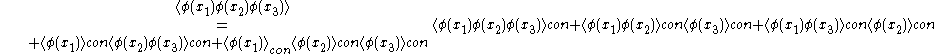
Assuming E is a convex functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
(which is debatable), the Legendre transformation
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
gives a one-to-one correspondence between the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of all source fields and its dual vector space, the configuration space of all φ fields. If E is not convex, we take the Fenchel conjugate instead. φ here is a classical field and not a quantum field operator.
Slightly out of the usual sign convention
Sign convention
In physics, a sign convention is a choice of the physical significance of signs for a set of quantities, in a case where the choice of sign is arbitrary. "Arbitrary" here means that the same physical system can be correctly described using different choices for the signs, as long as one set of...
s for Legendre transforms, the value
or
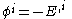
is associated to J. This agrees with the time ordered VEV <φ>J. The Legendre transform of E is the effective action (this corresponds to the rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
, which is the Fenchel conjugate of the cumulant-generating function, a common construction in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
; e.g. the Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
)
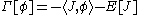
or
where
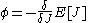
and
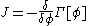
or
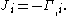
There are some caveats, though, the major one being we don't have a true one-to-one correspondence between the dual configuration spaces.
Tadpole (physics)
In quantum field theory, a tadpole is a one-loop Feynman diagram with one external leg, giving a contribution to a one-point correlation function . One-loop diagrams with a propagator that connects back to its originating vertex are often also referred as tadpoles...
, i.e.
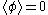for J=0. In that case, Γ[0] gives the zero-point energy, the first functional derivativeFunctional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
of Γ at φ=0 is zero, the second functional derivative gives the inverse of the full propagator, and the nth functional derivative for n ≥ 3 gives the one particle irreducible correlation functions or 1PI correlation functions. The Dyson equation relates the full propagator, the bare propagator and the 1PI self-energy. The n-point connected functions are given as the sum over all trees with n ≥ 3 1PI's as nodes and full propagators as edges.
But what if we have tadpoles? We can always adjust the source J so that there are no tadpoles, i.e.
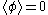. This corresponds to adding a Feynman rule corresponding to a coupling to the source. For any Feynman diagram, a subtadpole is a subgraph corresponding to a component not connected to any of the external legs which arises after cutting of an edge. Any Feynman diagram with a subtadpole can be evaluated as nonzero, but we can group these diagrams into equivalence classes (two connected diagrams are equivalent if they only vary in their subtadpoles). Therefore, we only need to consider the sum of all connected graphs without subtadpoles. The sum over all graphs in an equivalence class with subtadpoles is zero, since J is adjusted so that 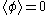. Any graph without subtadpoles do not contain any couplings to the source. A Taylor expansion of the effective action about φ = 0 gives the 1PI's corresponding to these value of the source according to the rules of the previous paragraph. So, we compute the 1PI's to get the Taylor series about 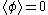. Then, from the effective action that we get from the Taylor series, we find the value of φ which minimizes the effective action. This gives us the VEV of φ when J = 0. Then, we now perform a Taylor series expansion about this VEV after shifting the field φ to a new field redefinition 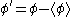(this is the background field methodBackground field method
In theoretical physics, background field method is a useful procedure to calculate the effective action of a quantum field theory by expanding a quantum field around a classical "background" value B:After this is done, the Green's functions are evaluated as a function of the background...
). Now we can compute the n-point correlations about the J = 0 vacuum.
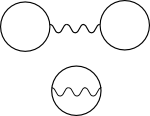
One loop approximation
The one-loop approximation to the effective action is