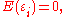Gauss–Markov theorem
Encyclopedia
In statistics
, the Gauss–Markov theorem, named after Carl Friedrich Gauss
and Andrey Markov
, states that in a linear regression model in which the errors have expectation zero and are uncorrelated
and have equal variance
s, the best linear unbiased
estimator
(BLUE) of the coefficients is given by the ordinary least squares
estimator. Here "best" means giving the lowest possible mean squared error
of the estimate. The errors need not be normal, nor independent and identically distributed (only uncorrelated
and homoscedastic).
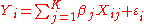
for i = 1, . . ., n, where β j are non-random but unobservable parameters, Xij are non-random and observable (called the "explanatory variables"), ε i are random, and so Y i are random. The random variables ε i are called the "errors
" (not to be confused with "residuals"; see errors and residuals in statistics
). Note that to include a constant in the model above, one can choose to include the variable XK all of whose observed values are unity: XiK = 1 for all i.
The Gauss–Markov assumptions state that
(i.e., all errors have the same variance; that is "homoscedasticity
"), and
for i ≠ j; that is, any two different values of the error term are drawn from "uncorrelated" distributions. A linear estimator of β j is a linear combination
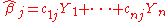
in which the coefficients cij are not allowed to depend on the underlying coefficients βj, since those are not observable, but are allowed to depend on the values Xij, since these data are observable. (The dependence of the coefficients on each Xij is typically nonlinear; the estimator is linear in each Yi and hence in each random εi, which is why this is "linear" regression
.) The estimator is said to be unbiased if and only if
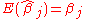
regardless of the values of Xij. Now, let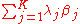
be some linear combination of the coefficients. Then the mean squared error
of the corresponding estimation is
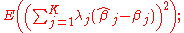
i.e., it is the expectation of the square of the weighted sum (across parameters) of the differences between the estimators and the corresponding parameters to be estimated. (Since we are considering the case in which all the parameter estimates are unbiased, this mean squared error is the same as the variance of the linear combination.) The best linear unbiased estimator (BLUE) of the vector β of parameters βj is one with the smallest mean squared error for every vector λ of linear combination parameters. This is equivalent to the condition that
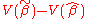
is a positive semi-definite matrix for every other linear unbiased estimator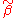
.
The ordinary least squares estimator (OLS) is the function
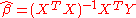
of Y and X that minimizes the sum of squares of residuals
(misprediction amounts):
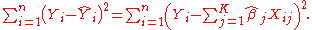
The theorem now states that the OLS estimator is a BLUE. The main idea of the proof is that the least-squares estimator is uncorrelated with every linear unbiased estimator of zero, i.e., with every linear combination
whose coefficients do not depend upon the unobservable β but whose expected value is always zero.
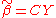be another linear estimator of 
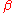and let C be given by 
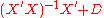, where D is a 
nonzero matrix. The goal is to show that such an estimator has a variance no smaller than that of 
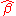, the OLS estimator.
The expectation of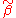
is: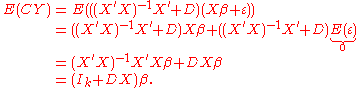
Therefore,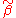
is unbiased if and only if 
.
The variance of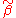
is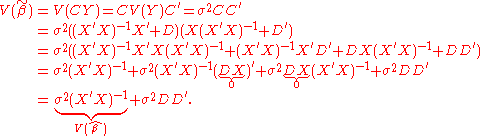
Since DD is a positive semidefinite matrix,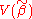
exceeds 
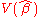by a positive semidefinite matrix.
(GLS) or Aitken
estimator extends the Gauss–Markov theorem to the case where the error vector has a non-scalar covariance matrixthe Aitken estimator is also a BLUE.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Gauss–Markov theorem, named after Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and Andrey Markov
Andrey Markov
Andrey Andreyevich Markov was a Russian mathematician. He is best known for his work on theory of stochastic processes...
, states that in a linear regression model in which the errors have expectation zero and are uncorrelated
Uncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
and have equal variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s, the best linear unbiased
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
(BLUE) of the coefficients is given by the ordinary least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
estimator. Here "best" means giving the lowest possible mean squared error
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
of the estimate. The errors need not be normal, nor independent and identically distributed (only uncorrelated
Uncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
and homoscedastic).
Statement
Suppose we have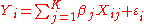for i = 1, . . ., n, where β j are non-random but unobservable parameters, Xij are non-random and observable (called the "explanatory variables"), ε i are random, and so Y i are random. The random variables ε i are called the "errors
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
" (not to be confused with "residuals"; see errors and residuals in statistics
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
). Note that to include a constant in the model above, one can choose to include the variable XK all of whose observed values are unity: XiK = 1 for all i.
The Gauss–Markov assumptions state that
(i.e., all errors have the same variance; that is "homoscedasticity
Homoscedasticity
In statistics, a sequence or a vector of random variables is homoscedastic if all random variables in the sequence or vector have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity...
"), and
for i ≠ j; that is, any two different values of the error term are drawn from "uncorrelated" distributions. A linear estimator of β j is a linear combination
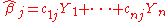
in which the coefficients cij are not allowed to depend on the underlying coefficients βj, since those are not observable, but are allowed to depend on the values Xij, since these data are observable. (The dependence of the coefficients on each Xij is typically nonlinear; the estimator is linear in each Yi and hence in each random εi, which is why this is "linear" regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
.) The estimator is said to be unbiased if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
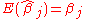
regardless of the values of Xij. Now, let
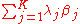be some linear combination of the coefficients. Then the mean squared errorMean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
of the corresponding estimation is
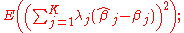
i.e., it is the expectation of the square of the weighted sum (across parameters) of the differences between the estimators and the corresponding parameters to be estimated. (Since we are considering the case in which all the parameter estimates are unbiased, this mean squared error is the same as the variance of the linear combination.) The best linear unbiased estimator (BLUE) of the vector β of parameters βj is one with the smallest mean squared error for every vector λ of linear combination parameters. This is equivalent to the condition that
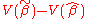
is a positive semi-definite matrix for every other linear unbiased estimator
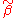.The ordinary least squares estimator (OLS) is the function
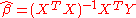
of Y and X that minimizes the sum of squares of residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
(misprediction amounts):
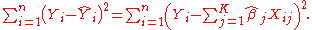
The theorem now states that the OLS estimator is a BLUE. The main idea of the proof is that the least-squares estimator is uncorrelated with every linear unbiased estimator of zero, i.e., with every linear combination
whose coefficients do not depend upon the unobservable β but whose expected value is always zero.
Proof
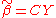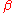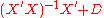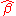Let be another linear estimator of and let C be given by , where D is a nonzero matrix. The goal is to show that such an estimator has a variance no smaller than that of , the OLS estimator.The expectation of
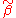is: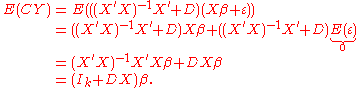Therefore,
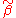is unbiased if and only if .The variance of
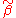is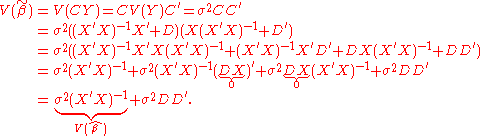Since DD is a positive semidefinite matrix,
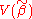exceeds 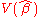by a positive semidefinite matrix.Generalized least squares estimator
The generalized least squaresGeneralized least squares
In statistics, generalized least squares is a technique for estimating the unknown parameters in a linear regression model. The GLS is applied when the variances of the observations are unequal , or when there is a certain degree of correlation between the observations...
(GLS) or Aitken
Alexander Aitken
Alexander Craig Aitken was one of New Zealand's greatest mathematicians. He studied for a PhD at the University of Edinburgh, where his dissertation, "Smoothing of Data", was considered so impressive that he was awarded a DSc in 1926, and was elected a fellow of the Royal Society of Edinburgh...
estimator extends the Gauss–Markov theorem to the case where the error vector has a non-scalar covariance matrixthe Aitken estimator is also a BLUE.
See also
- Independent and identically-distributed random variables
- Linear regressionLinear regressionIn statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
- Measurement uncertaintyMeasurement uncertaintyIn metrology, measurement uncertainty is a non-negative parameter characterizing the dispersion of the values attributed to a measured quantity. The uncertainty has a probabilistic basis and reflects incomplete knowledge of the quantity. All measurements are subject to uncertainty and a measured...
Other unbiased statistics
- Best linear unbiased predictionBest linear unbiased predictionIn statistics, best linear unbiased prediction is used in linear mixed models for the estimation of random effects. BLUP was derived by Charles Roy Henderson in 1950 but the term "best linear unbiased predictor" seems not to have been used until 1962...
(BLUP) - Minimum-variance unbiased estimatorMinimum-variance unbiased estimatorIn statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
(MVUE)
External links
- Earliest Known Uses of Some of the Words of Mathematics: G (brief history and explanation of the name)
- Proof of the Gauss Markov theorem for multiple linear regression (makes use of matrix algebra)
- A Proof of the Gauss Markov theorem using geometry