
Relative velocity
Encyclopedia
In non-relativistic kinematics
, relative velocity is the vector difference between the velocities
of two objects, as evaluated in terms of a single coordinate system
.
For example, if the velocities of particles A and B are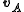 and
and 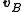 respectively in terms of a given coordinate system, then the relative velocity of A with respect to B (also called the velocity of A relative to B,
respectively in terms of a given coordinate system, then the relative velocity of A with respect to B (also called the velocity of A relative to B, 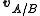 , or
, or 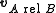 ) is
) is
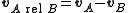 .
.
The expression "the velocity of A relative to B" is shorthand for "the velocity of A in the coordinate system where B is always at rest".
Conversely, the velocity of B relative to A is
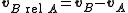 .
.
To be clear, the velocity of B "as seen from A" (which is to say,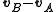 ) is another expression meaning "the velocity of B relative to A" or indeed "the velocity of B in the coordinate system where A is considered at rest"
) is another expression meaning "the velocity of B relative to A" or indeed "the velocity of B in the coordinate system where A is considered at rest"
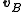 and Sara’s
and Sara’s 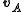 then
then
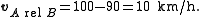
This is the velocity observed by Joe. Joe sees Sara moving at 10 km/h.
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, relative velocity is the vector difference between the velocities
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of two objects, as evaluated in terms of a single coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
.
For example, if the velocities of particles A and B are
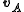 and
and 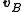 respectively in terms of a given coordinate system, then the relative velocity of A with respect to B (also called the velocity of A relative to B,
respectively in terms of a given coordinate system, then the relative velocity of A with respect to B (also called the velocity of A relative to B, 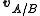 , or
, or 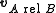 ) is
) is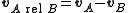 .
.The expression "the velocity of A relative to B" is shorthand for "the velocity of A in the coordinate system where B is always at rest".
Conversely, the velocity of B relative to A is
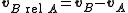 .
.To be clear, the velocity of B "as seen from A" (which is to say,
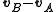 ) is another expression meaning "the velocity of B relative to A" or indeed "the velocity of B in the coordinate system where A is considered at rest"
) is another expression meaning "the velocity of B relative to A" or indeed "the velocity of B in the coordinate system where A is considered at rest"Example
Joe and Sara are driving in the same direction. Joe’s velocity is 90 km/h and Sara’s 100 km/h. If we take Joe’s velocity as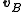 and Sara’s
and Sara’s 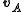 then
then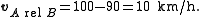
This is the velocity observed by Joe. Joe sees Sara moving at 10 km/h.

