Hereditarily finite set
Encyclopedia
In mathematics
and set theory
, hereditarily finite sets are defined recursively
as finite sets consisting of 0 or more hereditarily finite sets.
The set of all hereditarily finite sets is denoted Vω. If we denote P(S) for the power set of S, Vω can also be constructed by first taking the empty set written V0, then V1 = P(V0), V2 = P(V1),..., Vk = P(Vk−1),... Then
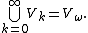
. They are a model
of the axioms consisting of the axioms of set theory with the axiom of infinity
replaced by its negation, thus proving that the axiom of infinity is not a consequence of the other axioms of set theory.
Notice that there are countably many hereditarily finite sets, since Vn is finite for any finite n (its cardinality is n−12, see tetration
), and the union of countably many finite sets is countable.
Equivalently, a set is hereditarily finite if and only if its transitive closure
is finite. Vω is also symbolized by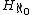
, meaning hereditarily of cardinality less than 
.
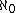Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, hereditarily finite sets are defined recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
as finite sets consisting of 0 or more hereditarily finite sets.
Formal definition
A recursive definition of a hereditarily finite set goes as follows:- Base case: The empty set is a hereditarily finite set.
- Recursion rule: If a1,...,ak are hereditarily finite, then so is {a1,...,ak}.
The set of all hereditarily finite sets is denoted Vω. If we denote P(S) for the power set of S, Vω can also be constructed by first taking the empty set written V0, then V1 = P(V0), V2 = P(V1),..., Vk = P(Vk−1),... Then
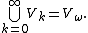
Discussion
The hereditarily finite sets are a subclass of the Von Neumann universeVon Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
. They are a model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of the axioms consisting of the axioms of set theory with the axiom of infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
replaced by its negation, thus proving that the axiom of infinity is not a consequence of the other axioms of set theory.
Notice that there are countably many hereditarily finite sets, since Vn is finite for any finite n (its cardinality is n−12, see tetration
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
), and the union of countably many finite sets is countable.
Equivalently, a set is hereditarily finite if and only if its transitive closure
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
is finite. Vω is also symbolized by
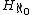, meaning hereditarily of cardinality less than .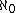