Ultralimit
Encyclopedia
In mathematics
, an ultralimit is a geometric construction that assigns to a sequence of metric space
s Xn a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces Xn and uses an ultrafilter
to avoid the process of repeatedly passing to subsequences to ensure convergence. An ultralimit is a generalization of the notion of Gromov-Hausdorff convergence
of metric spaces.
ω on the set of natural numbers
is a finite-additive set function (which can be thought of as a measure) 
from the power set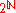 
(that is, the set of all subsets of 
) to the set {0,1} such that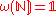 
.
An ultrafilter ω on
is non-principal if for every finite subset 
we have ω(F)=0.
.
If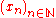
is a sequence of points in a metric space
(X,d) and x∈ X, the point x is called the ω -limit of xn , denoted
, if for every 
we have:
It is not hard to see the following:
An important basic fact states that, if (X,d) is a compact Hausdorff space and ω is a non-principal ultrafilter on
, the ω-limit of any sequence of points in X exists (and necessarily unique).
In particular, any bounded sequence of real numbers has a well-defined ω-limit in
(as closed intervals are compact).
. Let (Xn,dn) be a sequence of metric space
s with specified base-points pn∈Xn.
Let us say that a sequence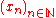
, where xn∈Xn, is admissible, if the sequence of real numbers (dn(xn,pn))n is bounded, that is, if there exists a positive real number C such that 
.
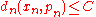Let us denote the set of all admissible sequences by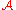
.
It is easy to see from the triangle inequality that for any two admissible sequences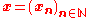
and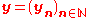 
the sequence (dn(xn,yn))n is bounded and hence there exists an ω-limit 
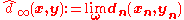. Let us define a relation 
on the set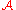 
the set of all admissible sequences as follows. For 
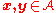we have 
whenever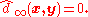 
It is easy to show that 
is an equivalence relation
on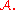
The ultralimit with respect to ω of the sequence (Xn,dn, pn) is a metric space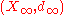
defined as follows.
As a set, we have
.
For two
-equivalence classes 
of admissible sequences 
and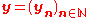 
we have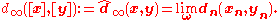 
It is not hard to see that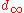
is well-defined and that it is a metric
on the set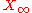
.
Denote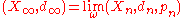
.
s of uniformly bounded diameter, that is, there exists a real number C>0 such that diam(Xn)≤C for every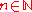
. Then for any choice pn of base-points in Xn every sequence 
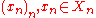is admissible. Therefore in this situation the choice of base-points does not have to be specified when defining an ultralimit, and the ultralimit 
depends only on (Xn,dn) and on ω but does not depend on the choice of a base-point sequence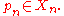 
. In this case one writes 
.
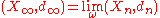Actually, by construction, the limit space is always complete even when (Xn,dn)
is a repeating sequence of a space (X,d) which is not complete.
and let pn ∈ X be a sequence of base-points. Then the ω – ultralimit of the sequence 
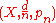is called the asymptotic cone of X with respect to ω and 
and is denoted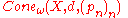 
. One often takes the base-point sequence to be constant pn=p for some p∈X; in this case the asymptotic cone does not depend on the choice of p∈X and is denoted by 
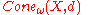or just 
.
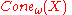The notion of an asymptotic cone plays an important role in geometric group theory
since asymptotic cones (or, more precisely, their topological types
and bi-Lipschitz types
) provide quasi-isometry
invariants of metric spaces in general and of finitely generated groups in particular. Asymptotic cones also turn out to be a useful tool in the study of relatively hyperbolic group
s and their generalizations.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an ultralimit is a geometric construction that assigns to a sequence of metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s Xn a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces Xn and uses an ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
to avoid the process of repeatedly passing to subsequences to ensure convergence. An ultralimit is a generalization of the notion of Gromov-Hausdorff convergence
Gromov-Hausdorff convergence
In mathematics, Gromov–Hausdorff convergence, named after Mikhail Gromov and Felix Hausdorff, is a notion for convergence of metric spaces which is a generalization of Hausdorff convergence.-Gromov–Hausdorff distance:...
of metric spaces.
Ultrafilters
Recall that an ultrafilterUltrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
ω on the set of natural numbers
is a finite-additive set function (which can be thought of as a measure) from the power set 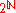(that is, the set of all subsets of ) to the set {0,1} such that 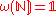.An ultrafilter ω on
is non-principal if for every finite subset we have ω(F)=0.Limit of a sequence of points with respect to an ultrafilter
Let ω be a non-principal ultrafilter on.If
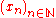is a sequence of points in a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(X,d) and x∈ X, the point x is called the ω -limit of xn , denoted
, if for every we have:It is not hard to see the following:
- If an ω -limit of a sequence of points exists, it is unique.
- If
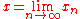in the standard sense, 
. (For this property to hold it is crucial that the ultrafilter be non-principal.)
An important basic fact states that, if (X,d) is a compact Hausdorff space and ω is a non-principal ultrafilter on
, the ω-limit of any sequence of points in X exists (and necessarily unique).In particular, any bounded sequence of real numbers has a well-defined ω-limit in
(as closed intervals are compact).Ultralimit of metric spaces with specified base-points
Let ω be a non-principal ultrafilter on. Let (Xn,dn) be a sequence of metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s with specified base-points pn∈Xn.
Let us say that a sequence
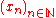, where xn∈Xn, is admissible, if the sequence of real numbers (dn(xn,pn))n is bounded, that is, if there exists a positive real number C such that 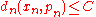.Let us denote the set of all admissible sequences by
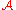.It is easy to see from the triangle inequality that for any two admissible sequences
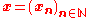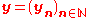and the sequence (dn(xn,yn))n is bounded and hence there exists an ω-limit 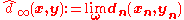. Let us define a relation on the set 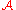the set of all admissible sequences as follows. For 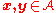we have whenever 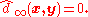It is easy to show that is an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on
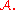
The ultralimit with respect to ω of the sequence (Xn,dn, pn) is a metric space
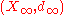defined as follows.As a set, we have
.For two
-equivalence classes of admissible sequences and 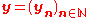we have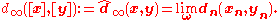 It is not hard to see that
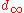is well-defined and that it is a metricMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
on the set
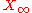.Denote
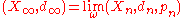.On basepoints in the case of uniformly bounded spaces
Suppose that (Xn,dn) is a sequence of metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s of uniformly bounded diameter, that is, there exists a real number C>0 such that diam(Xn)≤C for every
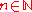. Then for any choice pn of base-points in Xn every sequence 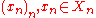is admissible. Therefore in this situation the choice of base-points does not have to be specified when defining an ultralimit, and the ultralimit depends only on (Xn,dn) and on ω but does not depend on the choice of a base-point sequence 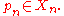. In this case one writes 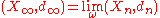.Basic properties of ultralimits
- If (Xn,dn) are geodesic metric spaces then
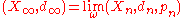is also a geodesic metric space. - If (Xn,dn) are complete metric spaces then
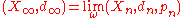is also a complete metric space.
Actually, by construction, the limit space is always complete even when (Xn,dn)
is a repeating sequence of a space (X,d) which is not complete.
- If (Xn,dn) are compact metric spaces that converge to a compact metric space (X,d) in the Gromov–Hausdorff sense (this automatically implies that the spaces (Xn,dn) have uniformly bounded diameter), then the ultralimit
is isometric to (X,d). - Suppose that (Xn,dn) are proper metric spaces and that
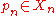are base-points such that the pointed sequence (Xn,dn,pn) converges to a proper metric space (X,d) in the Gromov–Hausdorff sense. Then the ultralimit 
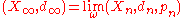is isometric to (X,d). - Let κ≤0 and let (Xn,dn) be a sequence of CAT(κ)-metric spacesCAT(k) spaceIn mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
. Then the ultralimit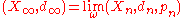
is also a CAT(κ)-space. - Let (Xn,dn) be a sequence of CAT(κn)-metric spacesCAT(k) spaceIn mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
where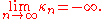
Then the ultralimit 
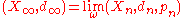is real treeReal treeA real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
.
Asymptotic cones
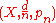An important class of ultralimits are the so-called asymptotic cones of metric spaces. Let (X,d) be a metric space, let ω be a non-principal ultrafilter on and let pn ∈ X be a sequence of base-points. Then the ω – ultralimit of the sequence is called the asymptotic cone of X with respect to ω and and is denoted 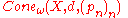. One often takes the base-point sequence to be constant pn=p for some p∈X; in this case the asymptotic cone does not depend on the choice of p∈X and is denoted by 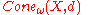or just 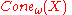.The notion of an asymptotic cone plays an important role in geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
since asymptotic cones (or, more precisely, their topological types
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
and bi-Lipschitz types
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
) provide quasi-isometry
Quasi-isometry
In mathematics, a quasi-isometry is a means to compare the large-scale structure of metric spaces. The concept is especially important in Gromov's geometric group theory.-Definition:...
invariants of metric spaces in general and of finitely generated groups in particular. Asymptotic cones also turn out to be a useful tool in the study of relatively hyperbolic group
Relatively hyperbolic group
In mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group...
s and their generalizations.
Examples
- Let (X,d) be a compact metric space and put (Xn,dn)=(X,d) for every
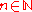. Then the ultralimit 
is isometric to (X,d). - Let (X,dX) and (Y,dY) be two distinct compact metric spaces and let (Xn,dn) be a sequence of metric spaces such that for each n either (Xn,dn)=(X,dX) or (Xn,dn)=(Y,dY). Let
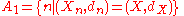and 
. Thus A1, A2 are disjoint and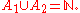 
Therefore one of A1, A2 has ω-measure 1 and the other has ω-measure 0. Hence 
is isometric to (X,dX) if ω(A1)=1 and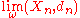 
is isometric to (Y,dY) if ω(A2)=1. This shows that the ultralimit can depend on the choice of an ultrafilter ω. - Let (M,g) be a compact connected Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
of dimension m, where g is a Riemannian metric on M. Let d be the metric on M corresponding to g, so that (M,d) is a geodesic metric space. Choose a basepoint p∈M. Then the ultralimit (and even the ordinary Gromov-Hausdorff limit)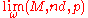
is isometric to the tangent spaceTangent spaceIn mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
TpM of M at p with the distance function on TpM given by the inner product g(p). Therefore the ultralimit
is isometric to the Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with the standard Euclidean metric. - Let
be the standard m-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with the standard Euclidean metric. Then the asymptotic cone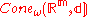
is isometric to 
. - Let
be the 2-dimensional integer latticeInteger latticeIn mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
where the distance between two lattice points is given by the length of the shortest edge-path between them in the grid. Then the asymptotic cone
is isometric to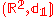 
where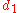 
is the Taxicab metric (or L1-metric) on 
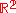. - Let (X,d) be a δ-hyperbolic geodesic metric space for some δ≥0. Then the asymptotic cone
is a real treeReal treeA real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
. - Let (X,d) be a metric space of finite diameter. Then the asymptotic cone
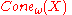is a single point. - Let (X,d) be a CAT(0)-metric spaceCAT(k) spaceIn mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
. Then the asymptotic cone
is also a CAT(0)-space.
Basic References
- John Roe. Lectures on Coarse Geometry. American Mathematical SocietyAmerican Mathematical SocietyThe American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
, 2003. ISBN 9780821833322; Ch. 7. - L.Van den Dries, A.J.Wilkie, On Gromov's theorem concerning groups of polynomial growth and elementary logic. Journal of AlgebraJournal of AlgebraJournal of Algebra is a leading international mathematical research journal in algebra. An imprint of Academic Press, it is presently published by Elsevier. Journal of Algebra was founded by Graham Higman, who was its editor from 1964 to 1984. From 1985 until 2000, Walter Feit served as its...
, Vol. 89(1984), pp. 349–374. - M. Kapovich B. Leeb. On asymptotic cones and quasi-isometry classes of fundamental groups of 3-manifolds, Geometric and Functional Analysis, Vol. 5 (1995), no. 3, pp. 582–603
- M. Kapovich. Hyperbolic Manifolds and Discrete Groups. Birkhäuser, 2000. ISBN 9780817639044; Ch. 9.
- Cornelia Druţu and Mark Sapir (with an Appendix by Denis Osin and Mark Sapir), Tree-graded spaces and asymptotic cones of groups. TopologyTopology (journal)Topology is a mathematical journal publishing scholarly articles related to topology and geometry. It was founded by J. H. C. Whitehead in 1962 and is published by Elsevier....
, Volume 44 (2005), no. 5, pp. 959–1058. - M. Gromov. Metric Structures for Riemannian and Non-Riemannian Spaces. Progress in Mathematics vol. 152, Birkhäuser, 1999. ISBN 0817638989; Ch. 3.
- B. Kleiner and B. Leeb, Rigidity of quasi-isometries for symmetric spaces and Euclidean buildings. Publications Mathématiques de L'IHÉSPublications Mathématiques de l'IHÉSPublications Mathématiques de l'IHÉS is a mathematical journal. It is published by Institut des Hautes Études Scientifiques, with the help of the Centre National de la Recherche Scientifique....
. Volume 86, Number 1, December 1997, pp. 115–197.