Type (model theory)
Encyclopedia
In model theory
and related areas of mathematics
, a type is a set of first-order
formulas in a language L with free variables x1, x2,…, xn which are true of a sequence of elements of an L-structure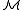
. Loosely speaking, types describe possible elements of a mathematical structure. Depending on the context, types can be complete or partial and they may use a fixed set of constants, A, from the structure 
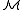. The question of which types represent actual elements of 
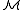leads to the ideas of saturated model
s and omitting types.
for a language
L. Let M be the universe of the structure. For every A ⊆ M, let L(A) be the language which is obtained from L by adding a constant ca for every a ∈ A. In other words,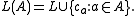
A 1-type (of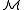
) over A is a set p(x) of formulas in L(A) with at most one free variable x (therefore 1-type) such that for every finite subset p0(x) ⊆ p(x) there is some b ∈ M, depending on p0(x), with 
(i.e. all formulas in p0(x) are true in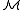 
when x is replaced by b).
Similarly an n-type (of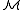
) over A is defined to be a set p(x1,…,xn) = p(x) of formulas in L(A) such that for every finite subset p0(x) ⊆ p(x) there are some elements b1,…,bn ∈ M with 
.
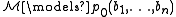Complete type refers to those types which are maximal with respect to inclusion, i.e. if p(x) is a complete type, then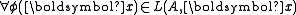
either 
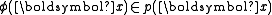or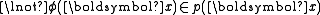 
. Any non-complete type is called a partial type.
So, the word type in general refers to any n-type, partial or complete, over any chosen set of parameters (possibly the empty set).
An n-type p(x) is said to be realized in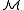
if there is an element b ∈ Mn such that 
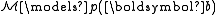. The existence of such a realization is guaranteed for any type by the Compactness theorem
, although the realization might take place in some elementary extension of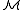
, rather than in 
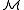itself.
If a complete type is realized by b in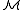
, then the type is typically denoted 
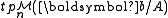and referred to as the complete type of b over A.
A type p(x) is said to be isolated by φ if there is a formula φ(x) with the property that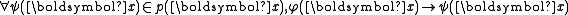
. Since finite subsets of a type are always realized in 
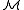, there is always an element b ∈ Mn such that φ(b) is true in 
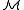; i.e. 
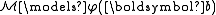, thus b realizes the entire isolated type. So isolated types will be realized in every elementary substructure or extension. Because of this, isolated types can never be omitted (see below).
A model that realizes the maximum possible variety of types is called a saturated model
, and the ultrapower
construction provides one way of producing saturated models.
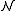have the natural numbers 
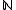as domain which are ordered by 
. Then 
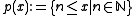is a type of 
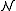over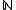 
: By definition 
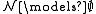anyhow. For every non-empty finite subset 
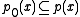, we can determine the maximal natural number 
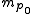occurring in 
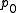and obtain 
.
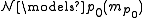The set p(x) is a partial type and claims "x is greater than any natural number". Yet such an element does not exist in the domain of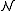
. This can be remedied by a new structure, 
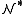say, with domain 
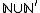where 
and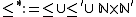 
.
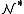is an elementary extension of 
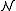(w.r.t. 
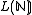) and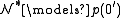 
. Hence 0' realises p(x). Of course, p(x) cannot be isolated in 
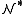or else it would be isolated in 
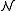since this is an elementary substructure of 
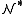. But being isolated in 
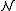means being realised in 
.
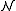Alternatively one could simply add another element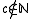
to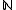 
and make c the greatest element. But then p(x) would be isolated by 
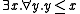in the extension of 
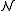. Hence this extension cannot be an elementary extension of 
.
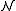Another example: the complete type of the number 2 over the emptyset, considered as a member of the natural numbers, would be the set of all first-order statements describing a variable x that are true for x = 2. This set would include formulas such as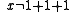
, 
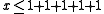, and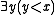 
. This is an example of an isolated type, since the formula 
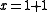implies all other formulas that are true about the number 2.
For example, the statements
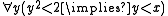
and
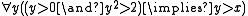
describing the square root of 2 are consistent with the axioms of ordered field
s, and can be extended to a complete type. This type is not realized in the ordered field of rational numbers, but is realized in the ordered field of reals. Similarly, the infinite set of formulas (over the emptyset) {x>1, x>1+1, x>1+1+1, ...} is not realized in the ordered field of real numbers, but is realized in the ordered field of hyperreals. If we allow more parameters, for instance all of the reals, we can specify a type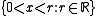
that is realized by an infinitesimal
hyperreal that violates the Archimedean property
.
The reason it is useful to restrict the parameters to a certain subset of the model is that it helps to distinguish the types that can be satisfied from those that cannot. For example, using the entire set of real numbers as parameters one could generate an uncountably infinite set of formulas like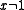
, 
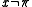, ... that would explicitly rule out every possible real value for x, and therefore could never be realized within the real numbers.
. Consider the following equivalence relation on formulae in the free variables x1,…, xn with parameters in M:
One can show that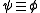
iff they are contained in exactly the same complete types.
The set of formulae in free variables x1,…,xn over A up to this equivalence relation is a Boolean algebra (and is canonically isomorphic to the set of A-definable subsets of Mn). The complete n-types correspond to ultrafilter
s of this boolean algebra. The set of complete n-types can be made into a topological space by taking the sets of types containing a given formula as basic open sets. This constructs the Stone space which is compact
, Hausdorff
, and totally disconnected
.
Example. The complete theory of algebraically closed field
s of characteristic
0 has quantifier elimination
which allows one to show that the possible complete 1-types correspond to:
In other words, the 1-types correspond exactly to the prime ideals of the polynomial ring Q[x] over the rationals Q: if r is an element of the model of type p, then the ideal corresponding to p is the set of polynomials with r as a root. More generally, the complete n-types correspond to the prime ideals of the polynomial ring Q[x1,...,xn], in other words to the points of the prime spectrum of this ring. (The Stone space topology can in fact be viewed as the Zariski topology of a Boolean ring induced in a natural way from the lattice structure of the Boolean Algebra; while the Zariski topology is not in general Hausdorff, it is in the case of Boolean rings.) For example, if q(x,y) is an irreducible polynomial in 2 variables, there is a 2-type whose realizations are (informally) pairs (x,y) of transcendental elements with q(x,y)=0.
If p is an isolated point
in the Stone space, i.e. if {p} is an open set, it is easy to see that every model realizes p (at least if the theory is complete). The omitting types theorem says that conversely if p is not isolated then there is a countable model omitting p (provided that the language is countable).
Example: In the theory of algebraically closed fields of characteristic 0, there is a 1-type represented by elements that are transcendental over the prime field. This is a non-isolated point of the Stone space (in fact, the only non-isolated point). The field of algebraic numbers is a model omitting this type, and the algebraic closure of any
transcendental extension of the rationals is a model realizing this type.
All the other types are "algebraic numbers" (more precisely, they are the sets of first order statements satisfied by some given algebraic number), and all such types are realized in all algebraically closed fields of characteristic 0.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a type is a set of first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
formulas in a language L with free variables x1, x2,…, xn which are true of a sequence of elements of an L-structure
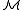. Loosely speaking, types describe possible elements of a mathematical structure. Depending on the context, types can be complete or partial and they may use a fixed set of constants, A, from the structure 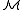. The question of which types represent actual elements of 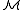leads to the ideas of saturated modelSaturated model
In mathematical logic, and particularly in its subfield model theory, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size...
s and omitting types.
Definition
Consider a structureStructure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
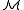for a languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
L. Let M be the universe of the structure. For every A ⊆ M, let L(A) be the language which is obtained from L by adding a constant ca for every a ∈ A. In other words,
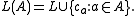
A 1-type (of
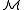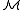) over A is a set p(x) of formulas in L(A) with at most one free variable x (therefore 1-type) such that for every finite subset p0(x) ⊆ p(x) there is some b ∈ M, depending on p0(x), with (i.e. all formulas in p0(x) are true in when x is replaced by b).Similarly an n-type (of
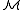) over A is defined to be a set p(x1,…,xn) = p(x) of formulas in L(A) such that for every finite subset p0(x) ⊆ p(x) there are some elements b1,…,bn ∈ M with 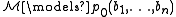.Complete type refers to those types which are maximal with respect to inclusion, i.e. if p(x) is a complete type, then
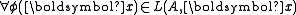eithe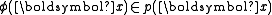r or 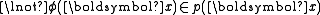. Any non-complete type is called a partial type.So, the word type in general refers to any n-type, partial or complete, over any chosen set of parameters (possibly the empty set).
An n-type p(x) is said to be realized in
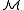if there is an element b ∈ Mn such that 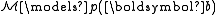. The existence of such a realization is guaranteed for any type by the Compactness theoremCompactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
, although the realization might take place in some elementary extension of
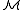, rather than in 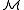itself.If a complete type is realized by b in
, then the type is typically denoted 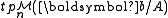and referred to as the complete type of b over A.A type p(x) is said to be isolated by φ if there is a formula φ(x) with the property that
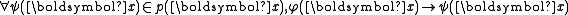. Since finite subsets of a type are always realized in 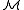, there is always an element b ∈ Mn such that φ(b) is true in 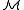; i.e. 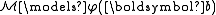, thus b realizes the entire isolated type. So isolated types will be realized in every elementary substructure or extension. Because of this, isolated types can never be omitted (see below).A model that realizes the maximum possible variety of types is called a saturated model
Saturated model
In mathematical logic, and particularly in its subfield model theory, a saturated model M is one which realizes as many complete types as may be "reasonably expected" given its size...
, and the ultrapower
Ultraproduct
The ultraproduct is a mathematical construction that appears mainly in abstract algebra and in model theory, a branch of mathematical logic. An ultraproduct is a quotient of the direct product of a family of structures. All factors need to have the same signature...
construction provides one way of producing saturated models.
Examples of types
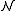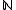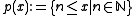Let have the natural numbers as domain which are ordered by . Then is a type of 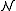over 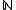: By definition 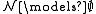anyhow. For every non-empty finite subset 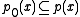, we can determine the maximal natural number 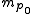occurring in 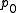and obtain 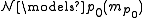.The set p(x) is a partial type and claims "x is greater than any natural number". Yet such an element does not exist in the domain of
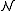. This can be remedied by a new structure, 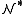say, with domain 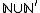where and 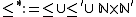. 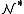is an elementary extension of 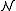(w.r.t. 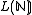) and 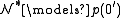. Hence 0' realises p(x). Of course, p(x) cannot be isolated in 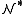or else it would be isolated in 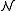since this is an elementary substructure of 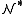. But being isolated in 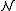means being realised in 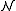.Alternatively one could simply add another element
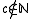to 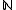and make c the greatest element. But then p(x) would be isolated by 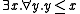in the extension of 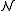. Hence this extension cannot be an elementary extension of 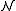.Another example: the complete type of the number 2 over the emptyset, considered as a member of the natural numbers, would be the set of all first-order statements describing a variable x that are true for x = 2. This set would include formulas such as
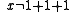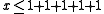, , and 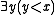. This is an example of an isolated type, since the formula 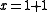implies all other formulas that are true about the number 2.For example, the statements
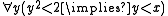
and
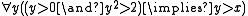
describing the square root of 2 are consistent with the axioms of ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
s, and can be extended to a complete type. This type is not realized in the ordered field of rational numbers, but is realized in the ordered field of reals. Similarly, the infinite set of formulas (over the emptyset) {x>1, x>1+1, x>1+1+1, ...} is not realized in the ordered field of real numbers, but is realized in the ordered field of hyperreals. If we allow more parameters, for instance all of the reals, we can specify a type
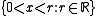that is realized by an infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
hyperreal that violates the Archimedean property
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
.
The reason it is useful to restrict the parameters to a certain subset of the model is that it helps to distinguish the types that can be satisfied from those that cannot. For example, using the entire set of real numbers as parameters one could generate an uncountably infinite set of formulas like
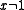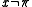, , ... that would explicitly rule out every possible real value for x, and therefore could never be realized within the real numbers.Stone spaces
It is useful to consider the set of complete n-types over A as a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. Consider the following equivalence relation on formulae in the free variables x1,…, xn with parameters in M:
One can show that
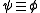iff they are contained in exactly the same complete types.The set of formulae in free variables x1,…,xn over A up to this equivalence relation is a Boolean algebra (and is canonically isomorphic to the set of A-definable subsets of Mn). The complete n-types correspond to ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
s of this boolean algebra. The set of complete n-types can be made into a topological space by taking the sets of types containing a given formula as basic open sets. This constructs the Stone space which is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, and totally disconnected
Totally disconnected space
In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
.
Example. The complete theory of algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
s of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0 has quantifier elimination
Quantifier elimination
Quantifier elimination is a concept of simplification used in mathematical logic, model theory, and theoretical computer science. One way of classifying formulas is by the amount of quantification...
which allows one to show that the possible complete 1-types correspond to:
- Roots of a given irreducible non-constant polynomialIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over the rationals with leading coefficient 1. For example, the type of square roots of 2. Each of these types is an open point of the Stone space. - Transcendental elements, that are not roots of any non-zero polynomial. This type is a point in the Stone space that is closed but not open.
In other words, the 1-types correspond exactly to the prime ideals of the polynomial ring Q[x] over the rationals Q: if r is an element of the model of type p, then the ideal corresponding to p is the set of polynomials with r as a root. More generally, the complete n-types correspond to the prime ideals of the polynomial ring Q[x1,...,xn], in other words to the points of the prime spectrum of this ring. (The Stone space topology can in fact be viewed as the Zariski topology of a Boolean ring induced in a natural way from the lattice structure of the Boolean Algebra; while the Zariski topology is not in general Hausdorff, it is in the case of Boolean rings.) For example, if q(x,y) is an irreducible polynomial in 2 variables, there is a 2-type whose realizations are (informally) pairs (x,y) of transcendental elements with q(x,y)=0.
The omitting types theorem
Given a complete n-type p one can ask if there is a model of the theory that omits p, in other words there is no n-tuple in the model which realizes p.If p is an isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
in the Stone space, i.e. if {p} is an open set, it is easy to see that every model realizes p (at least if the theory is complete). The omitting types theorem says that conversely if p is not isolated then there is a countable model omitting p (provided that the language is countable).
Example: In the theory of algebraically closed fields of characteristic 0, there is a 1-type represented by elements that are transcendental over the prime field. This is a non-isolated point of the Stone space (in fact, the only non-isolated point). The field of algebraic numbers is a model omitting this type, and the algebraic closure of any
transcendental extension of the rationals is a model realizing this type.
All the other types are "algebraic numbers" (more precisely, they are the sets of first order statements satisfied by some given algebraic number), and all such types are realized in all algebraically closed fields of characteristic 0.