
Digital root
Encyclopedia
The digital root of a number is the (single digit) value obtained by an iterative process of summing digits
, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached.
For example, the digital root of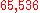 is
is 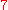 , because
, because  and
and 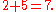
Digital roots can be calculated with congruence
s rather than by adding up all the digits, a procedure that can save time in the case of very large numbers.
Digital roots can be used as a sort of checksum
. For example, since the digital root of a sum is always equal to the digital root of the sum of the summands' digital roots. A person adding long columns of large numbers will often find it reassuring to apply casting out nines
to his or her result—knowing that this technique will catch the majority of errors.
Digital roots are used in Western numerology
, but certain numbers deemed to have occult significance (such as 11 and 22) are not always completely reduced to a single digit.
The number of times the digits must be summed to reach the digital sum is called a number's additive persistence
; in the above example, the additive persistence of 65,536 is 2.
 as the position
as the position  holds with respect to the last multiple of nine to the left of
holds with respect to the last multiple of nine to the left of  . For example, the digital root of 11 is 2, which means that 11 is the second number after 9. The digital root of 23 is 5, this means that 23 is the fifth number after a multiple of nine to the left of 23; in this case, 18. The digital root of 2035 is 1 which means that 2035-1, that is 2034, is a multiple of nine.
. For example, the digital root of 11 is 2, which means that 11 is the second number after 9. The digital root of 23 is 5, this means that 23 is the fifth number after a multiple of nine to the left of 23; in this case, 18. The digital root of 2035 is 1 which means that 2035-1, that is 2034, is a multiple of nine.
The digital roots of {1,2,3,4,5,6,7,8} which are the same digits themselves, reveal their position with respect to 0. The digital roots of nine and all of its multiples are nine, however, they all play the same role that zero plays for the integers from 1 to 8. It helps to think of the number nine and all its multiples as a kind of zero or zeros, so that the other integers be able to reveal their position or digital roots with respect to them. This is in part the nature of the decimal system.
With this in mind we may think of the digital root of the positive integer as
as 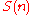 , defined by:
, defined by:
which precisely says that,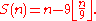
This formula will give the digital root of and will assign the value 0 to all
and will assign the value 0 to all  which are multiples of nine.
which are multiples of nine.
in the decimal system. You can see that for example, 2x5=1; that's because the digital root of 10 is 1 or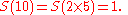
The table shows a number of interesting patterns and symmetries and is known as the Vedic square
.
 denote the sum of the digits of
denote the sum of the digits of  . Eventually the sequence
. Eventually the sequence 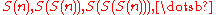 becomes constant. Let
becomes constant. Let  (the digital sum of
(the digital sum of  ) represent this constant value.
) represent this constant value.
 .
.

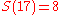
Thus,
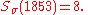
For simplicity let us agree simply that
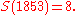
 eventually becomes constant? Here's a proof:
eventually becomes constant? Here's a proof:
Let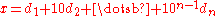 , with
, with  (For all
(For all 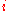 ,
,  is an integer
is an integer
greater than or equal to and less than
and less than  ). Then,
). Then,  . This means that
. This means that 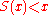 , unless
, unless  , in which case
, in which case  is a one-digit number. Thus, repeatedly using the
is a one-digit number. Thus, repeatedly using the 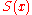 function would cause
function would cause  to decrease by at least 1, until it becomes a one-digit number, at which point it will stay constant, as
to decrease by at least 1, until it becomes a one-digit number, at which point it will stay constant, as 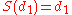 .
.
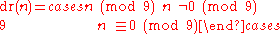
or,
To generalize the concept of digital roots to other bases b, one can simply change the 9 in the formula to b - 1.
The digital root is the value modulo 9 because and thus
and thus  so regardless of position, the value mod 9 is the same –
so regardless of position, the value mod 9 is the same –  – which is why digits can be meaningfully added. Concretely, for a three-digit number,
– which is why digits can be meaningfully added. Concretely, for a three-digit number,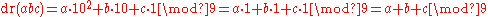
To obtain the modular value with respect to other numbers n, one can take weighted sums, where the weight on the kth digit corresponds to the value of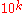 modulo n, or analogously for
modulo n, or analogously for 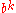 for different bases. This is simplest for 2, 5, and 10, where higher digits vanish (since 2 and 5 divide 10), which corresponds to the familiar fact that the divisibility of a decimal number with respect to 2, 5, and 10 can be checked by the last digit (even numbers end in 0, 2, 4, 6, or 8).
for different bases. This is simplest for 2, 5, and 10, where higher digits vanish (since 2 and 5 divide 10), which corresponds to the familiar fact that the divisibility of a decimal number with respect to 2, 5, and 10 can be checked by the last digit (even numbers end in 0, 2, 4, 6, or 8).
Also of note is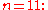 since
since 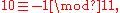 and thus
and thus  taking the alternating sum of digits yields the value modulo 11.
taking the alternating sum of digits yields the value modulo 11.
Digit sum
In mathematics, the digit sum of a given integer is the sum of all its digits,...
, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached.
For example, the digital root of
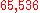 is
is 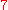 , because
, because  and
and 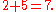
Digital roots can be calculated with congruence
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
s rather than by adding up all the digits, a procedure that can save time in the case of very large numbers.
Digital roots can be used as a sort of checksum
Checksum
A checksum or hash sum is a fixed-size datum computed from an arbitrary block of digital data for the purpose of detecting accidental errors that may have been introduced during its transmission or storage. The integrity of the data can be checked at any later time by recomputing the checksum and...
. For example, since the digital root of a sum is always equal to the digital root of the sum of the summands' digital roots. A person adding long columns of large numbers will often find it reassuring to apply casting out nines
Casting out nines
Casting out nines is a sanity check to ensure that hand computations of sums, differences, products, and quotients of integers are correct. By looking at the digital roots of the inputs and outputs, the casting-out-nines method can help one check arithmetic calculations...
to his or her result—knowing that this technique will catch the majority of errors.
Digital roots are used in Western numerology
Numerology
Numerology is any study of the purported mystical relationship between a count or measurement and life. It has many systems and traditions and beliefs...
, but certain numbers deemed to have occult significance (such as 11 and 22) are not always completely reduced to a single digit.
The number of times the digits must be summed to reach the digital sum is called a number's additive persistence
Persistence of a number
In mathematics, the persistence of a number is a term used to describe the number of times one must apply a given operation to an integer before reaching a fixed point, i.e...
; in the above example, the additive persistence of 65,536 is 2.
Significance and formula of the digital root
It helps to see the digital root of any positive integer as the position
as the position  holds with respect to the last multiple of nine to the left of
holds with respect to the last multiple of nine to the left of  . For example, the digital root of 11 is 2, which means that 11 is the second number after 9. The digital root of 23 is 5, this means that 23 is the fifth number after a multiple of nine to the left of 23; in this case, 18. The digital root of 2035 is 1 which means that 2035-1, that is 2034, is a multiple of nine.
. For example, the digital root of 11 is 2, which means that 11 is the second number after 9. The digital root of 23 is 5, this means that 23 is the fifth number after a multiple of nine to the left of 23; in this case, 18. The digital root of 2035 is 1 which means that 2035-1, that is 2034, is a multiple of nine.The digital roots of {1,2,3,4,5,6,7,8} which are the same digits themselves, reveal their position with respect to 0. The digital roots of nine and all of its multiples are nine, however, they all play the same role that zero plays for the integers from 1 to 8. It helps to think of the number nine and all its multiples as a kind of zero or zeros, so that the other integers be able to reveal their position or digital roots with respect to them. This is in part the nature of the decimal system.
With this in mind we may think of the digital root of the positive integer
 as
as 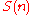 , defined by:
, defined by:
which precisely says that,
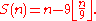
This formula will give the digital root of
 and will assign the value 0 to all
and will assign the value 0 to all  which are multiples of nine.
which are multiples of nine.Abstract multiplication of digital roots
The table below shows the digital roots produced by the familiar multiplication tableMultiplication table
In mathematics, a multiplication table is a mathematical table used to define a multiplication operation for an algebraic system....
in the decimal system. You can see that for example, 2x5=1; that's because the digital root of 10 is 1 or
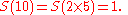
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 2 | 4 | 6 | 8 | 1 | 3 | 5 | 7 | 9 |
| 3 | 3 | 6 | 9 | 3 | 6 | 9 | 3 | 6 | 9 |
| 4 | 4 | 8 | 3 | 7 | 2 | 6 | 1 | 5 | 9 |
| 5 | 5 | 1 | 6 | 2 | 7 | 3 | 8 | 4 | 9 |
| 6 | 6 | 3 | 9 | 6 | 3 | 9 | 6 | 3 | 9 |
| 7 | 7 | 5 | 3 | 1 | 8 | 6 | 4 | 2 | 9 |
| 8 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 9 |
| 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
The table shows a number of interesting patterns and symmetries and is known as the Vedic square
Vedic square
In ancient Indian mathematics, a Vedic square is a variation on a typical 9 × 9 multiplication table. The entry in each cell is the digital root of the product of the column and row headings i.e...
.
Formal definition
Let denote the sum of the digits of
denote the sum of the digits of  . Eventually the sequence
. Eventually the sequence 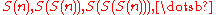 becomes constant. Let
becomes constant. Let  (the digital sum of
(the digital sum of  ) represent this constant value.
) represent this constant value.Example
Let us find the digital sum of .
.
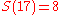
Thus,
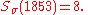
For simplicity let us agree simply that
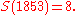
Proof that a constant value exists
How do we know that the sequence eventually becomes constant? Here's a proof:
eventually becomes constant? Here's a proof:Let
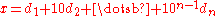 , with
, with  (For all
(For all 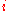 ,
,  is an integer
is an integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
greater than or equal to
 and less than
and less than  ). Then,
). Then,  . This means that
. This means that 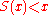 , unless
, unless  , in which case
, in which case  is a one-digit number. Thus, repeatedly using the
is a one-digit number. Thus, repeatedly using the 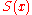 function would cause
function would cause  to decrease by at least 1, until it becomes a one-digit number, at which point it will stay constant, as
to decrease by at least 1, until it becomes a one-digit number, at which point it will stay constant, as 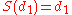 .
.Congruence formula
The formula is: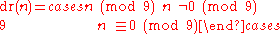
or,

To generalize the concept of digital roots to other bases b, one can simply change the 9 in the formula to b - 1.
The digital root is the value modulo 9 because
 and thus
and thus  so regardless of position, the value mod 9 is the same –
so regardless of position, the value mod 9 is the same –  – which is why digits can be meaningfully added. Concretely, for a three-digit number,
– which is why digits can be meaningfully added. Concretely, for a three-digit number,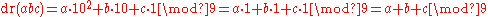
To obtain the modular value with respect to other numbers n, one can take weighted sums, where the weight on the kth digit corresponds to the value of
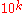 modulo n, or analogously for
modulo n, or analogously for 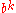 for different bases. This is simplest for 2, 5, and 10, where higher digits vanish (since 2 and 5 divide 10), which corresponds to the familiar fact that the divisibility of a decimal number with respect to 2, 5, and 10 can be checked by the last digit (even numbers end in 0, 2, 4, 6, or 8).
for different bases. This is simplest for 2, 5, and 10, where higher digits vanish (since 2 and 5 divide 10), which corresponds to the familiar fact that the divisibility of a decimal number with respect to 2, 5, and 10 can be checked by the last digit (even numbers end in 0, 2, 4, 6, or 8).Also of note is
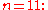 since
since 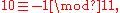 and thus
and thus  taking the alternating sum of digits yields the value modulo 11.
taking the alternating sum of digits yields the value modulo 11.Some properties of digital roots
- Digital root of a squareSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
is 1, 4, 7, or 9. - Digital root of a perfect cube is 1, 8 or 9.
- Digital root of a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
(except 3) is 1, 2, 4, 5, 7, or 8. - Digital root of a power of 2Power of twoIn mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
is 1, 2, 4, 5, 7, or 8. Digital roots of the powers of 2 progress in the sequence 1, 2, 4, 8, 7, 5, 1. This even applies to powers less than 1; for example, 2 to the power of 0 is 1; 2 to the power of -1 (minus one) is .5, with a digital root of 5; 2 to the power of -2 is .25, with a digital root of 7; and so on, ad infinitum in both directions. - Digital root of an even perfect numberPerfect numberIn number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
(except 6) is 1. - Digital root of a star numberStar numberA star number is a centered figurate number that represents a centered hexagram, such as the one that Chinese checkers is played on.The nth star number is given by the formula 6n + 1...
is 1 or 4. - Digital root of a nonzero multipleMultiple (mathematics)In mathematics, a multiple is the product of any quantity and an integer. In other words, for the quantities a and b, we say that b is a multiple of a if b = na for some integer n , which is called the multiplier or coefficient. If a is not zero, this is equivalent to saying that b/a is an integer...
of 9 is 9. - Digital root of a nonzero multipleMultiple (mathematics)In mathematics, a multiple is the product of any quantity and an integer. In other words, for the quantities a and b, we say that b is a multiple of a if b = na for some integer n , which is called the multiplier or coefficient. If a is not zero, this is equivalent to saying that b/a is an integer...
of 3 is 3, 6 or 9. - Digital root of a triangular numberTriangular numberA triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
is 1, 3, 6 or 9. - Digital root of a factorialFactorialIn mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
≥ 6! is 9. - Digital root of Fibonacci Series is a repeating pattern of 1, 1, 2, 3, 5, 8, 4, 3, 7, 1, 8, 9, 8, 8, 7, 6, 4, 1, 5, 6, 2, 8, 1, 9.
- Digital root of the product of twin primesTwin primeA twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
, other than 3 and 5, is 8. The digital root of the product of 3 and 5 (twin primes) is 6. - Digital root of a non-zero number is 9 if and only if the number is itself a multipleMultipleThe word multiple can refer to:*Multiple , multiples of numbers*List of multiple discoveries, instances of scientists, working independently of each other, reaching similar findings...
of 9

