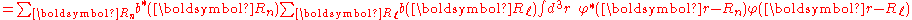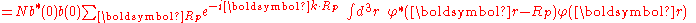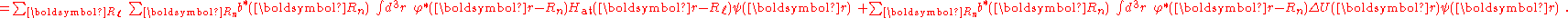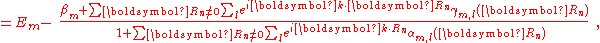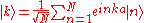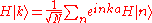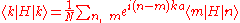Tight binding (physics)
Encyclopedia
In solid-state physics
, the tight binding model (or TB model) is an approach to the calculation of electronic band structure
using an approximate set of wave functions based upon superposition
of wave functions for isolated atom
s located at each atomic site. The method is closely related to the LCAO method
used in chemistry. Tight binding models are applied to a wide variety of solids. The model gives good qualitative results in many cases and can be combined with other models that give better results where the tight binding model fails. Though the tight binding model is a one-electron model, the model also provides a basis for more advanced calculations like the calculation of surface states
and application to various kinds of many-body problem
and quasiparticle
calculations.
suggests that this quantum mechanical model
describes the properties of tightly bound electrons in solids. The electron
s in this model should be tightly bound to the atom
to which they belong and they should have limited interaction with states and potentials on surrounding atoms of the solid. As a result the wave function of the electron will be rather similar to the atomic orbital
of the free atom it belongs to. The energy of the electron will also be rather close to the ionization energy
of the electron in the free atom or ion because the interaction with potentials and states on neighboring atoms is limited.
Though the mathematical formulation of the one-particle tight binding Hamiltonian
may look complicated at first glance, the model is not complicated at all and can be understood intuitively quite easily. There are only three kinds of elements that play a significant role in the theory. Two of those three kinds of elements should be close to zero and can often be neglected. The most important elements in the model are the inter atomic matrix elements, which would simply be called the bond energies
by a chemist.
In general there are a number of atomic energy levels
and atomic orbitals involved in the model. This can lead to complicated band structures because the orbitals belong to different point group
representations. The reciprocal lattice
and the Brillouin zone
often belong to a different space group
than the crystal
of the solid. High symmetry points in the Brillouin zone belong to different point group representations. When simple systems are studied, like the lattices of elements or simple compounds, it is often not very difficult to calculate eigenstates in high symmetry points analytically. So the tight binding model can provide nice examples for those who want to learn more about group theory
.
What is known as the "tight binding model" has a long history and has been applied in many ways and with many different purposes and different outcomes. The model doesn't stand on its own. Parts of the model can be filled in or extended by other kinds of calculations and models like the nearly-free electron model
. The model itself, or parts of it, can serve as the basis for other calculations. In the study of conductive polymer
s, organic semiconductor
s and molecular electronics
for example, tight binding like models are applied in which the role of the atoms in the original concept is replaced by the molecular orbital
s of conjugated system
s and where the inter atomic matrix elements are replaced by inter or intra molecular hopping and tunneling parameters. These conductors nearly all have very anisotropic properties and sometimes are almost perfectly one-dimensional.
, who was influenced considerably by the work of Friedrich Hund
. The LCAO method for approximating molecular orbitals was introduced in 1928 by B. N. Finklestein and G. E. Horowitz, while the LCAO method for solids was developed by Felix Bloch
, as part of his doctoral dissertation in 1928, concurrently with and independent of the LCAO-MO approach. A much simpler interpolation scheme for approximating the electronic band structure, especially for the d-bands of transition metal
s, is the parameterized tight-binding method conceived in 1954 by John Clarke Slater
and George Fred Koster, the absolute climax in the history of this model. Hence, it is sometimes referred to as the SK tight-binding method. With the SK tight-binding method, electronic band structure calculations on a solid need not be carried out with full rigor as in the original Bloch's theorem
but, rather, first-principles calculations are carried out only at high-symmetry points and the band structure is interpolated over the remainder of the Brillouin zone
between these points.
In this approach, interactions between different atomic sites are considered as perturbation
s. There exist several kinds of interactions we must consider. The crystal Hamiltonian
is only approximately a sum of atomic Hamiltonians located at different sites and atomic wave functions overlap adjacent atomic sites in the crystal, and so are not accurate representations of the exact wave function. There are further explanations in the next section with some mathematical expressions.
Recently, in the research about strongly correlated material
, the tight binding approach is basic approximation because highly localized electrons like 3-d transition metal
electrons sometimes display strongly correlated behaviors. In this case, the role of electron-electron interaction must be considered using the many-body physics
description.
The tight-binding model is typically used for calculations of electronic band structure
and band gap
s in the static regime. However, in combination with other methods such as the random phase approximation
(RPA) model, the dynamic response of systems may also be studied.
s
, which are eigenfunction
s of the Hamiltonian
Hat of a single isolated atom. When the atom is placed in a crystal, this atomic wave function overlaps adjacent atomic sites, and so are not true eigenfunctions of the crystal Hamiltonian. The overlap is less when electrons are tightly bound, which is the source of the descriptor "tight-binding". Any corrections to the atomic potential ΔU required to obtain the true Hamiltonian H of the system, are assumed small:
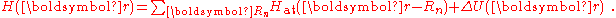
A solution ψ(r) to the time-independent single electron Schrödinger equation
is then approximated as a linear combination of atomic orbitals
:
,
where m refers to the m-th atomic energy level and Rn locates an atomic site in the crystal lattice
.
of the crystal implies the wave function under translation can change only by a phase factor:
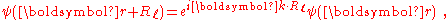
where k is the wave vector
of the wave function. Consequently, the coefficients satisfy
By substituting Rp = Rn − Rℓ, we find
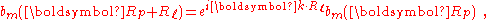
or
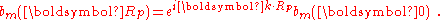
Normalizing the wave function to unity:
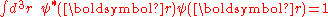
so the normalization sets b(0) as
where α (Rp ) are the atomic overlap integrals, which frequently are neglected resulting in
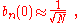
and
is important for the m-th energy band, the Bloch energies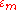
are of the form
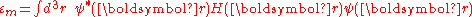
Here terms involving the atomic Hamiltonian at sites other than where it is centered are neglected. The energy then becomes
where Em is the energy of the m-th atomic level, and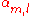
, 
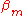and 
are the tight binding matrix elements.
,
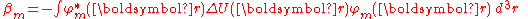is the atomic energy shift due to the potential on neighboring atoms. This term is relatively small in most cases. If it is large it means that potentials on neighboring atoms have a large influence on the energy of the central atom.
The next term
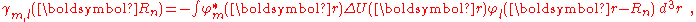
is the inter atomic matrix element between the atomic orbitals m and l on adjacent atoms. It is also called the bond energy or two center integral and it is the most important element in the tight binding model.
The last terms
,
denote the overlap integrals
between the atomic orbitals m and l on adjacent atoms.
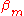-matrix elements are not so large in comparison with the ionization energy because the potentials of neighboring atoms on the central atom are limited. If 
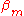is not relatively small it means that the potential of the neighboring atom on the central atom is not small either. In that case it is an indication that the tight binding model is not a very good model for the description of the band structure for some reason. The inter atomic distances can be too small or the charges on the atoms or ions in the lattice is wrong for example.
The inter atomic matrix elements
can be calculated directly if the atomic wave functions and the potentials are known in detail. Most often this is not the case. There are numerous ways to get parameters for these matrix elements. Parameters can be obtained from chemical bond energy data. Energies and eigenstates on some high symmetry points in the Brillouin zone
can be evaluated and values integrals in the matrix elements can be matched with band structure data from other sources.
The inter atomic overlap matrix elements
should be rather small or neglectable. If they are large it is again an indication that the tight binding model is of limited value for some purposes. Large overlap is an indication for too short inter atomic distance for example. In metals and transition metals the broad s-band or sp-band can be fitted better to an existing band structure calculation by the introduction of next-nearest-neighbor matrix elements and overlap integrals but fits like that don't yield a very useful model for the electronic wave function of a metal. Broad bands in dense materials are better described by a nearly free electron model.
The tight binding model works particularly well in cases where the band width is small and the electrons are strongly localized, like in the case of d-bands and f-bands. The model also gives good results in the case of open crystal structures, like diamond or silicon, where the number of neighbors is small. The model can easily be combined with a nearly free electron model in a hybrid NFE-TB model.
functions describe the electronic states in a periodic crystal lattice
. Bloch functions can be represented as a Fourier series
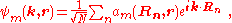
where Rn denotes an atomic site in a periodic crystal lattice, k is the wave vector
of the Bloch wave, r is the electron position, m is the band index, and the sum is over all N atomic sites. The Bloch wave is an exact eigensolution for the wave function of an electron in a periodic crystal potential corresponding to an energy Em (k), and is spread over the entire crystal volume.
Using the Fourier transform
analysis, a spatially localized wave function for the m-th energy band can be derived from this Bloch wave:
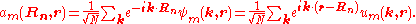
These real space wave functions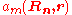
are called Wannier function
s, and are fairly closely localized to the atomic site Rn. Of course, if we have exact Wannier function
s, the exact Bloch functions can be derived using the inverse Fourier transform.
However it is not easy to calculate directly either Bloch functions
or Wannier function
s. An approximate approach is necessary in the calculation of electronic structures of solids. If we consider the extreme case of isolated atoms, the Wannier function would become an isolated atomic orbital. That limit suggests the choice of an atomic wave function as an approximate form for the Wannier function, the so-called tight binding approximation.
and Hubbard model
are based on tight binding model. If we introduce second quantization formalism, it is clear to understand the concept of tight binding model.
Using the atomic orbital as a basis state, we can establish the second quantization Hamiltonian operator in tight binding model.
Here, hopping integral
corresponds to the transfer integral 
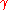in tight binding model. Considering extreme cases of 
, it is impossible for electron to hop into neighboring sites. This case is the isolated atomic system. If the hopping term is turned on (
) electrons can stay in both sites lowering their kinetic energy
.
In the strongly correlated electron system, it is necessary to consider the electron-electron interaction. This term can be written in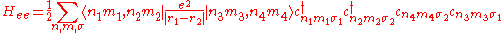
This interaction Hamiltonian includes direct Coulomb
interaction energy and exchange interaction energy between electrons. There are several novel physics induced from this electron-electron interaction energy, such as metal-insulator transition
s (MIT), high-temperature superconductivity
, and several quantum phase transition
s.
between atomic sites.
To find approximate eigenstates of the Hamiltonian, we can use a linear combination of the atomic orbitals
where N = total number of sites and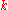
is a real parameter with 
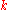. (This wave function is normalized to unity by the leading factor 1/√N provided overlap of atomic wave functions is ignored.) Assuming only nearest neighbor overlap, the only non-zero matrix elements of the Hamiltonian can be expressed as
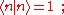
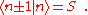
The energy Ei is the ionization energy corresponding to the chosen atomic orbital and U is the energy shift of the orbital as a result of the potential of neighboring atoms. The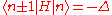
elements, which are the Slater and Koster interatomic matrix elements, are the bond energies
. In this one dimensional s-band model we only have 
-bonds between the s-orbitals with bond energy 
. The overlap between states on neighboring atoms is S. We can derive the energy of the state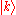 
using the above equation:
where, for example,
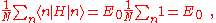
and
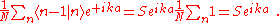
Thus the energy of this state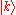
can be represented in the familiar form of the energy dispersion:
.
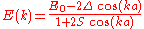This example is readily extended to three dimensions, for example, to a body-centered cubic or face-centered cubic lattice by introducing the nearest neighbor vector locations in place of simply n a. Likewise, the method can be extended to multiple bands using multiple different atomic orbitals at each site. The general formulation above shows how these extensions can be accomplished.
d-bands, a table of inter atomic matrix elements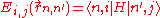
which, with a little patience and effort, can also be derived from the cubic harmonic orbitals
straightforwardly. The table expresses the matrix elements as functions of LCAO two-centre bond integrals
between two cubic harmonic
orbitals, i and j, on adjacent atoms. The bond integrals are for example the
, 
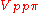and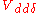 
for sigma
, pi
and delta
bonds.
The inter atomic vector is expressed as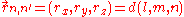
where d is the distance between the atoms and l, m and n are the direction cosine
s to the neighboring atom.
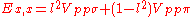
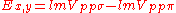
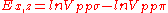
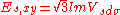
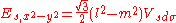
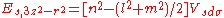
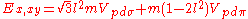
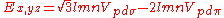
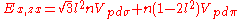
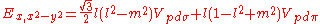
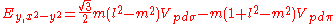
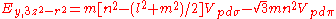
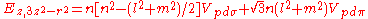
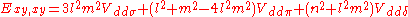
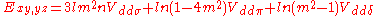
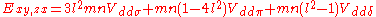
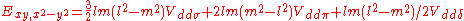
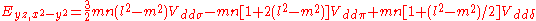
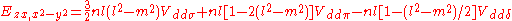
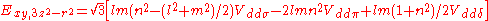
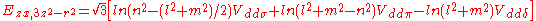
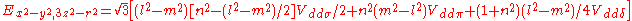
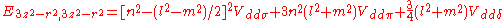
Not all inter atomic matrix elements are listed explicitly. Matrix elements that are not listed in this table can be constructed by permutation of indices and cosine directions of other matrix elements in the table.
Solid-state physics
Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...
, the tight binding model (or TB model) is an approach to the calculation of electronic band structure
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
using an approximate set of wave functions based upon superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of wave functions for isolated atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s located at each atomic site. The method is closely related to the LCAO method
Linear combination of atomic orbitals molecular orbital method
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions...
used in chemistry. Tight binding models are applied to a wide variety of solids. The model gives good qualitative results in many cases and can be combined with other models that give better results where the tight binding model fails. Though the tight binding model is a one-electron model, the model also provides a basis for more advanced calculations like the calculation of surface states
Surface states
Surface states are electronic states found at the surface of materials. They are formed due to the sharp transition from solid material that ends with a surface and are found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the...
and application to various kinds of many-body problem
Many-body problem
The many-body problem is a general name for a vast category of physical problems pertaining to the properties of microscopic systems made of a large number of interacting particles. Microscopic here implies that quantum mechanics has to be used to provide an accurate description of the system...
and quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
calculations.
Introduction
The name "tight binding" of this electronic band structure modelElectronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
suggests that this quantum mechanical model
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
describes the properties of tightly bound electrons in solids. The electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in this model should be tightly bound to the atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
to which they belong and they should have limited interaction with states and potentials on surrounding atoms of the solid. As a result the wave function of the electron will be rather similar to the atomic orbital
Atomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
of the free atom it belongs to. The energy of the electron will also be rather close to the ionization energy
Ionization energy
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove an electron from the species to a practically infinite distance. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.The property...
of the electron in the free atom or ion because the interaction with potentials and states on neighboring atoms is limited.
Though the mathematical formulation of the one-particle tight binding Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
may look complicated at first glance, the model is not complicated at all and can be understood intuitively quite easily. There are only three kinds of elements that play a significant role in the theory. Two of those three kinds of elements should be close to zero and can often be neglected. The most important elements in the model are the inter atomic matrix elements, which would simply be called the bond energies
Bond energy
In chemistry, bond energy is the measure of bond strength in a chemical bond. It is the heat required to break one Mole of molecules into their individual atoms. For example, the carbon-hydrogen bond energy in methane E is the enthalpy change involved with breaking up one molecule of methane into...
by a chemist.
In general there are a number of atomic energy levels
Energy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
and atomic orbitals involved in the model. This can lead to complicated band structures because the orbitals belong to different point group
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
representations. The reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
and the Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
often belong to a different space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
than the crystal
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
of the solid. High symmetry points in the Brillouin zone belong to different point group representations. When simple systems are studied, like the lattices of elements or simple compounds, it is often not very difficult to calculate eigenstates in high symmetry points analytically. So the tight binding model can provide nice examples for those who want to learn more about group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
.
What is known as the "tight binding model" has a long history and has been applied in many ways and with many different purposes and different outcomes. The model doesn't stand on its own. Parts of the model can be filled in or extended by other kinds of calculations and models like the nearly-free electron model
Nearly-free electron model
In solid-state physics, the nearly-free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual Empty Lattice Approximation...
. The model itself, or parts of it, can serve as the basis for other calculations. In the study of conductive polymer
Conductive polymer
Conductive polymers or, more precisely, intrinsically conducting polymers are organic polymers that conduct electricity. Such compounds may have metallic conductivity or can be semiconductors. The biggest advantage of conductive polymers is their processability, mainly by dispersion. Conductive...
s, organic semiconductor
Organic semiconductor
An organic semiconductor is an organic material with semiconductor properties. Single molecules, short chain and organic polymers can be semiconductive. Semiconducting small molecules include the polycyclic aromatic compounds pentacene, anthracene, and rubrene...
s and molecular electronics
Molecular electronics
Molecular electronics, sometimes called moletronics, involves the study and application of molecular building blocks for the fabrication of electronic components...
for example, tight binding like models are applied in which the role of the atoms in the original concept is replaced by the molecular orbital
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
s of conjugated system
Conjugated system
In chemistry, a conjugated system is a system of connected p-orbitals with delocalized electrons in compounds with alternating single and multiple bonds, which in general may lower the overall energy of the molecule and increase stability. Lone pairs, radicals or carbenium ions may be part of the...
s and where the inter atomic matrix elements are replaced by inter or intra molecular hopping and tunneling parameters. These conductors nearly all have very anisotropic properties and sometimes are almost perfectly one-dimensional.
Historical background
By 1928, the idea of a molecular orbital had been advanced by Robert MullikenRobert S. Mulliken
Robert Sanderson Mulliken was an American physicist and chemist, primarily responsible for the early development of molecular orbital theory, i.e. the elaboration of the molecular orbital method of computing the structure of molecules. Dr. Mulliken received the Nobel Prize for chemistry in 1966...
, who was influenced considerably by the work of Friedrich Hund
Friedrich Hund
Friedrich Hermann Hund was a German physicist from Karlsruhe known for his work on atoms and molecules.Hund worked at the Universities of Rostock, Leipzig, Jena, Frankfurt am Main, and Göttingen....
. The LCAO method for approximating molecular orbitals was introduced in 1928 by B. N. Finklestein and G. E. Horowitz, while the LCAO method for solids was developed by Felix Bloch
Felix Bloch
Felix Bloch was a Swiss physicist, working mainly in the U.S.-Life and work:Bloch was born in Zürich, Switzerland to Jewish parents Gustav and Agnes Bloch. He was educated there and at the Eidgenössische Technische Hochschule, also in Zürich. Initially studying engineering he soon changed to physics...
, as part of his doctoral dissertation in 1928, concurrently with and independent of the LCAO-MO approach. A much simpler interpolation scheme for approximating the electronic band structure, especially for the d-bands of transition metal
Transition metal
The term transition metal has two possible meanings:*The IUPAC definition states that a transition metal is "an element whose atom has an incomplete d sub-shell, or which can give rise to cations with an incomplete d sub-shell." Group 12 elements are not transition metals in this definition.*Some...
s, is the parameterized tight-binding method conceived in 1954 by John Clarke Slater
John C. Slater
John Clarke Slater was a noted American physicist who made major contributions to the theory of the electronic structure of atoms, molecules and solids. This work is of ongoing importance in chemistry, as well as in many areas of physics. He also made major contributions to microwave electronics....
and George Fred Koster, the absolute climax in the history of this model. Hence, it is sometimes referred to as the SK tight-binding method. With the SK tight-binding method, electronic band structure calculations on a solid need not be carried out with full rigor as in the original Bloch's theorem
Bloch's theorem
* For the theorem named after Felix Bloch on wave functions of a particle in a periodic potential, see Bloch wave.* For the theorem in complex variables named after André Bloch, see Bloch's theorem ....
but, rather, first-principles calculations are carried out only at high-symmetry points and the band structure is interpolated over the remainder of the Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
between these points.
In this approach, interactions between different atomic sites are considered as perturbation
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
s. There exist several kinds of interactions we must consider. The crystal Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is only approximately a sum of atomic Hamiltonians located at different sites and atomic wave functions overlap adjacent atomic sites in the crystal, and so are not accurate representations of the exact wave function. There are further explanations in the next section with some mathematical expressions.
Recently, in the research about strongly correlated material
Strongly correlated material
Strongly correlated materials are a wide class of electronic materials that show unusual electronic and magnetic properties, such as metal-insulator transitions or half-metallicity...
, the tight binding approach is basic approximation because highly localized electrons like 3-d transition metal
Transition metal
The term transition metal has two possible meanings:*The IUPAC definition states that a transition metal is "an element whose atom has an incomplete d sub-shell, or which can give rise to cations with an incomplete d sub-shell." Group 12 elements are not transition metals in this definition.*Some...
electrons sometimes display strongly correlated behaviors. In this case, the role of electron-electron interaction must be considered using the many-body physics
Many-body theory
The many-body theory is an area of physics which provides the framework for understanding the collective behavior of vast assemblies of interacting particles. In general terms, the many-body theory deals with effects that manifest themselves only in systems containing large numbers of constituents...
description.
The tight-binding model is typically used for calculations of electronic band structure
Electronic band structure
In solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
and band gap
Band gap
In solid state physics, a band gap, also called an energy gap or bandgap, is an energy range in a solid where no electron states can exist. In graphs of the electronic band structure of solids, the band gap generally refers to the energy difference between the top of the valence band and the...
s in the static regime. However, in combination with other methods such as the random phase approximation
Random phase approximation
The random phase approximation is an approximation method in condensed matter physics and in nuclear physics. It was first introduced by David Bohm and David Pines as an important result in a series of seminal papers. For decades physicists had been trying to incorporate the effect of microscopic...
(RPA) model, the dynamic response of systems may also be studied.
Mathematical formulation
We introduce the atomic orbitalAtomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
s
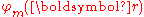, which are eigenfunctionEigenfunction
In mathematics, an eigenfunction of a linear operator, A, defined on some function space is any non-zero function f in that space that returns from the operator exactly as is, except for a multiplicative scaling factor. More precisely, one has...
s of the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
Hat of a single isolated atom. When the atom is placed in a crystal, this atomic wave function overlaps adjacent atomic sites, and so are not true eigenfunctions of the crystal Hamiltonian. The overlap is less when electrons are tightly bound, which is the source of the descriptor "tight-binding". Any corrections to the atomic potential ΔU required to obtain the true Hamiltonian H of the system, are assumed small:
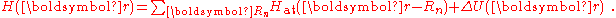
A solution ψ(r) to the time-independent single electron Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is then approximated as a linear combination of atomic orbitals
Linear combination of atomic orbitals molecular orbital method
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions...
:,where m refers to the m-th atomic energy level and Rn locates an atomic site in the crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
.
Translational symmetry and normalization
The translational symmetryTranslational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
of the crystal implies the wave function under translation can change only by a phase factor:
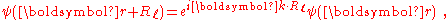
where k is the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
of the wave function. Consequently, the coefficients satisfy
By substituting Rp = Rn − Rℓ, we find
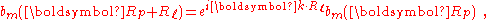
or
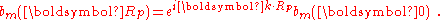
Normalizing the wave function to unity:
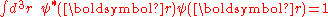
so the normalization sets b(0) as
where α (Rp ) are the atomic overlap integrals, which frequently are neglected resulting in
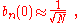
and
The tight binding Hamiltonian
Using the tight binding form for the wave function, and assuming only the m-th atomic energy levelEnergy level
A quantum mechanical system or particle that is bound -- that is, confined spatially—can only take on certain discrete values of energy. This contrasts with classical particles, which can have any energy. These discrete values are called energy levels...
is important for the m-th energy band, the Bloch energies
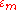are of the form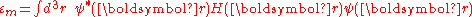
Here terms involving the atomic Hamiltonian at sites other than where it is centered are neglected. The energy then becomes
where Em is the energy of the m-th atomic level, and
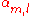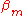, and are the tight binding matrix elements.The tight binding matrix elements
The element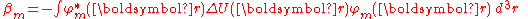,is the atomic energy shift due to the potential on neighboring atoms. This term is relatively small in most cases. If it is large it means that potentials on neighboring atoms have a large influence on the energy of the central atom.
The next term
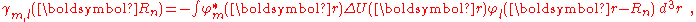
is the inter atomic matrix element between the atomic orbitals m and l on adjacent atoms. It is also called the bond energy or two center integral and it is the most important element in the tight binding model.
The last terms
,denote the overlap integrals
Overlap matrix
The overlap matrix is a square matrix, used in quantum chemistry to describe the inter-relationship of a set of basis vectors of a quantum system. In particular, if the vectors are orthogonal to one another, the overlap matrix will be diagonal. In addition, if the basis vectors form an...
between the atomic orbitals m and l on adjacent atoms.
Evaluation of the matrix elements
As mentioned before the values of the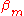-matrix elements are not so large in comparison with the ionization energy because the potentials of neighboring atoms on the central atom are limited. If 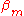is not relatively small it means that the potential of the neighboring atom on the central atom is not small either. In that case it is an indication that the tight binding model is not a very good model for the description of the band structure for some reason. The inter atomic distances can be too small or the charges on the atoms or ions in the lattice is wrong for example.The inter atomic matrix elements
can be calculated directly if the atomic wave functions and the potentials are known in detail. Most often this is not the case. There are numerous ways to get parameters for these matrix elements. Parameters can be obtained from chemical bond energy data. Energies and eigenstates on some high symmetry points in the Brillouin zoneBrillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
can be evaluated and values integrals in the matrix elements can be matched with band structure data from other sources.
The inter atomic overlap matrix elements
should be rather small or neglectable. If they are large it is again an indication that the tight binding model is of limited value for some purposes. Large overlap is an indication for too short inter atomic distance for example. In metals and transition metals the broad s-band or sp-band can be fitted better to an existing band structure calculation by the introduction of next-nearest-neighbor matrix elements and overlap integrals but fits like that don't yield a very useful model for the electronic wave function of a metal. Broad bands in dense materials are better described by a nearly free electron model.The tight binding model works particularly well in cases where the band width is small and the electrons are strongly localized, like in the case of d-bands and f-bands. The model also gives good results in the case of open crystal structures, like diamond or silicon, where the number of neighbors is small. The model can easily be combined with a nearly free electron model in a hybrid NFE-TB model.
Connection to Wannier functions
Bloch waveBloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
functions describe the electronic states in a periodic crystal lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
. Bloch functions can be represented as a Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
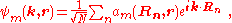
where Rn denotes an atomic site in a periodic crystal lattice, k is the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
of the Bloch wave, r is the electron position, m is the band index, and the sum is over all N atomic sites. The Bloch wave is an exact eigensolution for the wave function of an electron in a periodic crystal potential corresponding to an energy Em (k), and is spread over the entire crystal volume.
Using the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
analysis, a spatially localized wave function for the m-th energy band can be derived from this Bloch wave:
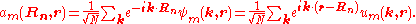
These real space wave functions
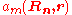are called Wannier functionWannier function
The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier.The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes...
s, and are fairly closely localized to the atomic site Rn. Of course, if we have exact Wannier function
Wannier function
The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier.The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes...
s, the exact Bloch functions can be derived using the inverse Fourier transform.
However it is not easy to calculate directly either Bloch functions
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
or Wannier function
Wannier function
The Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier.The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes...
s. An approximate approach is necessary in the calculation of electronic structures of solids. If we consider the extreme case of isolated atoms, the Wannier function would become an isolated atomic orbital. That limit suggests the choice of an atomic wave function as an approximate form for the Wannier function, the so-called tight binding approximation.
Second quantization
Modern explanations of electronic structure like t-J modelT-J model
The t-J model was first derived in 1977 from the Hubbard model by Józef Spałek. The model describes strongly correlated electron systems. It is used to calculate high temperature superconductivity states in doped antiferromagnets.The t-J Hamiltonian is:...
and Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
are based on tight binding model. If we introduce second quantization formalism, it is clear to understand the concept of tight binding model.
Using the atomic orbital as a basis state, we can establish the second quantization Hamiltonian operator in tight binding model.
-
, -
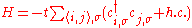- creation and annihilation operators
-
- spin polarization
-
- hopping integral
-
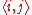-nearest neighbor index
Here, hopping integral
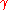corresponds to the transfer integral in tight binding model. Considering extreme cases of , it is impossible for electron to hop into neighboring sites. This case is the isolated atomic system. If the hopping term is turned on () electrons can stay in both sites lowering their kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
.
In the strongly correlated electron system, it is necessary to consider the electron-electron interaction. This term can be written in
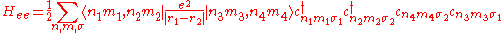
This interaction Hamiltonian includes direct Coulomb
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
interaction energy and exchange interaction energy between electrons. There are several novel physics induced from this electron-electron interaction energy, such as metal-insulator transition
Metal-insulator transition
Metal-insulator transitions are transitions from a metal to an insulator...
s (MIT), high-temperature superconductivity
High-temperature superconductivity
High-temperature superconductors are materials that have a superconducting transition temperature above . From 1960 to 1980, 30 K was thought to be the highest theoretically possible Tc...
, and several quantum phase transition
Quantum phase transition
In physics, a quantum phase transition is a phase transition between different quantum phases . Contrary to classical phase transitions, quantum phase transitions can only be accessed by varying a physical parameter - such as magnetic field or pressure - at absolute zero temperature...
s.
Example: one-dimensional s-band
Here the tight binding model is illustrated with a s-band model for a string of atoms with a single s-orbital in a straight line with spacing a and σ bondsSigma bond
In chemistry, sigma bonds are the strongest type of covalent chemical bond. They are formed by head-on overlapping between atomic orbitals. Sigma bonding is most clearly defined for diatomic molecules using the language and tools of symmetry groups. In this formal approach, a σ-bond is...
between atomic sites.
To find approximate eigenstates of the Hamiltonian, we can use a linear combination of the atomic orbitals
where N = total number of sites and
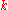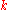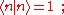
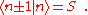
is a real parameter with . (This wave function is normalized to unity by the leading factor 1/√N provided overlap of atomic wave functions is ignored.) Assuming only nearest neighbor overlap, the only non-zero matrix elements of the Hamiltonian can be expressed as The energy Ei is the ionization energy corresponding to the chosen atomic orbital and U is the energy shift of the orbital as a result of the potential of neighboring atoms. The
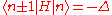elements, which are the Slater and Koster interatomic matrix elements, are the bond energiesChemical bond
A chemical bond is an attraction between atoms that allows the formation of chemical substances that contain two or more atoms. The bond is caused by the electromagnetic force attraction between opposite charges, either between electrons and nuclei, or as the result of a dipole attraction...
. In this one dimensional s-band model we only have -bonds between the s-orbitals with bond energy . The overlap between states on neighboring atoms is S. We can derive the energy of the state 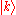using the above equation:
where, for example,
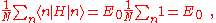
and
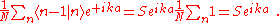
Thus the energy of this state
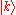can be represented in the familiar form of the energy dispersion: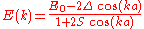.- For
the energy is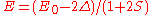 
and the state consists of a sum of all atomic orbitals. This state can be viewed as a chain of bonding orbitalsMolecular orbitalIn chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
. - For
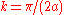the energy is 
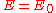and the state consists of a sum of atomic orbitals which are a factor 
out of phase. This state can be viewed as a chain of non-bonding orbitalNon-bonding orbitalA non-bonding orbital, also known as non-bonding molecular orbital and sometimes designated by the letter n in molecular orbital diagrams, is a molecular orbital whose occupation by electrons neither increases nor decreases the bond order between the involved atoms...
s. - Finally for
the energy is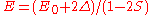 
and the state consists of an alternating sum of atomic orbitals. This state can be viewed as a chain of anti-bonding orbitalsAntibondingAntibonding is a type of chemical bonding. An antibonding orbital is a form of molecular orbital that is located outside the region of two distinct nuclei...
.
This example is readily extended to three dimensions, for example, to a body-centered cubic or face-centered cubic lattice by introducing the nearest neighbor vector locations in place of simply n a. Likewise, the method can be extended to multiple bands using multiple different atomic orbitals at each site. The general formulation above shows how these extensions can be accomplished.
Table of interatomic matrix elements
In 1954 J.C. Slater and F.G. Koster published, mainly for the calculation of transition metalTransition metal
The term transition metal has two possible meanings:*The IUPAC definition states that a transition metal is "an element whose atom has an incomplete d sub-shell, or which can give rise to cations with an incomplete d sub-shell." Group 12 elements are not transition metals in this definition.*Some...
d-bands, a table of inter atomic matrix elements
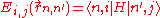
which, with a little patience and effort, can also be derived from the cubic harmonic orbitals
Cubic harmonic
In fields like computational chemistry and solid-state and condensed matter physics the so called atomic orbitals, or spin-orbitals, as they appear in textbooks on quantum physics, are often partially replaced by cubic harmonics for a number of reasons....
straightforwardly. The table expresses the matrix elements as functions of LCAO two-centre bond integrals
Chemical bond
A chemical bond is an attraction between atoms that allows the formation of chemical substances that contain two or more atoms. The bond is caused by the electromagnetic force attraction between opposite charges, either between electrons and nuclei, or as the result of a dipole attraction...
between two cubic harmonic
Cubic harmonic
In fields like computational chemistry and solid-state and condensed matter physics the so called atomic orbitals, or spin-orbitals, as they appear in textbooks on quantum physics, are often partially replaced by cubic harmonics for a number of reasons....
orbitals, i and j, on adjacent atoms. The bond integrals are for example the
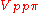, and 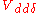for sigmaSigma bond
In chemistry, sigma bonds are the strongest type of covalent chemical bond. They are formed by head-on overlapping between atomic orbitals. Sigma bonding is most clearly defined for diatomic molecules using the language and tools of symmetry groups. In this formal approach, a σ-bond is...
, pi
Pi bond
In chemistry, pi bonds are covalent chemical bonds where two lobes of one involved atomic orbital overlap two lobes of the other involved atomic orbital...
and delta
Delta bond
In chemistry, delta bonds are chemical bonds of the covalent type, where four lobes of one involved atomic orbital overlap four lobes of the other involved atomic orbital...
bonds.
The inter atomic vector is expressed as
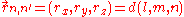
where d is the distance between the atoms and l, m and n are the direction cosine
Direction cosine
In analytic geometry, the direction cosines of a vector are the cosines of the angles between the vector and the three coordinate axes. Or equivalently it is the component contributions to the unit vector....
s to the neighboring atom.
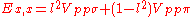
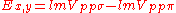
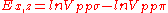
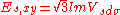
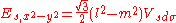
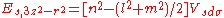
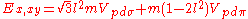
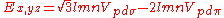
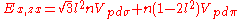
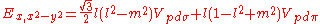
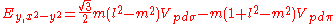
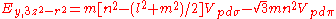
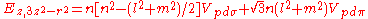
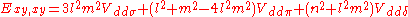
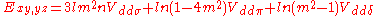
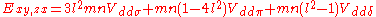
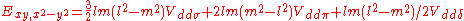
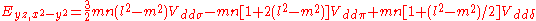
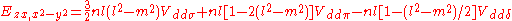
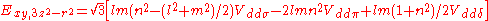
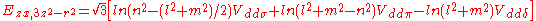
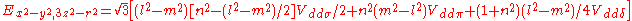
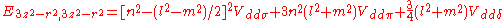
Not all inter atomic matrix elements are listed explicitly. Matrix elements that are not listed in this table can be constructed by permutation of indices and cosine directions of other matrix elements in the table.
See also
- Electronic band structureElectronic band structureIn solid-state physics, the electronic band structure of a solid describes those ranges of energy an electron is "forbidden" or "allowed" to have. Band structure derives from the diffraction of the quantum mechanical electron waves in a periodic crystal lattice with a specific crystal system and...
- Nearly-free electron modelNearly-free electron modelIn solid-state physics, the nearly-free electron model is a quantum mechanical model of physical properties of electrons that can move almost freely through the crystal lattice of a solid. The model is closely related to the more conceptual Empty Lattice Approximation...
- Bloch waveBloch waveA Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
s - Kronig-Penney model
- Fermi surfaceFermi surfaceIn condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
- Wannier functionWannier functionThe Wannier functions are a complete set of orthogonal functions used in solid-state physics. They were introduced by Gregory Wannier.The Wannier functions for different lattice sites in a crystal are orthogonal, allowing a convenient basis for the expansion of electron states in certain regimes...
- Hubbard modelHubbard modelThe Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
- t-J modelT-J modelThe t-J model was first derived in 1977 from the Hubbard model by Józef Spałek. The model describes strongly correlated electron systems. It is used to calculate high temperature superconductivity states in doped antiferromagnets.The t-J Hamiltonian is:...
- Effective massEffective massIn solid state physics, a particle's effective mass is the mass it seems to carry in the semiclassical model of transport in a crystal. It can be shown that electrons and holes in a crystal respond to electric and magnetic fields almost as if they were particles with a mass dependence in their...
- Anderson's ruleAnderson's ruleAnderson's rule is used for the construction of energy band diagrams of the heterojunction between two semiconductor materials. It is also referred to as the electron affinity rule. Anderson's rule was first described by R. L...
- Dynamical theory of diffractionDynamical theory of diffractionThe dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems...
- Solid state physics
- Linear combination of atomic orbitals molecular orbital methodLinear combination of atomic orbitals molecular orbital methodA linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions...
(LCAO)