In fields like computational chemistry

Computational chemistry

Computational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...

 and solid-state

Solid-state physics

Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...

 and condensed matter

Condensed matter physics

Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...

 physics the so called atomic orbitals, or spin-orbitals, as they appear in textbooks on quantum physics, are often partially replaced by cubic harmonics for a number of reasons.

Introduction

The hydrogen-like atomic orbitals

Hydrogen-like atom

A hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...

 with principal quantum number and angular momentum quantum number 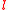are often expressed as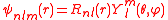


in which the 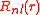is the radial part of the wave function and is the angular dependent part. The are the spherical harmonics

Spherical harmonics

In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...

, which are solutions of the angular momentum

Angular momentum

In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...

 operator. The spherical harmonics are representations of functions of the full rotation group

Rotation group

In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...

 SO(3) with rotational symmetry. In many fields of physics and chemistry these spherical harmonics are replaced by cubic harmonics because the rotational symmetry of the atom and its environment are distorted or because cubic harmonics offer computational benefits.

Symmetry and coordinate system

In many cases, especially in chemistry

Chemistry

Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....

 and solid-state

Solid-state physics

Solid-state physics is the study of rigid matter, or solids, through methods such as quantum mechanics, crystallography, electromagnetism, and metallurgy. It is the largest branch of condensed matter physics. Solid-state physics studies how the large-scale properties of solid materials result from...

 and condensed-matter physics, the system under investigation doesn't have rotational symmetry. Often it has some kind of lower symmetry, with a special point group

Point groups in three dimensions

In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...

representation, or it has no spatial symmetry at all. Biological and biochemical

Biochemistry

Biochemistry, sometimes called biological chemistry, is the study of chemical processes in living organisms, including, but not limited to, living matter. Biochemistry governs all living organisms and living processes...

 systems, like amino acid

Amino acid

Amino acids are molecules containing an amine group, a carboxylic acid group and a side-chain that varies between different amino acids. The key elements of an amino acid are carbon, hydrogen, oxygen, and nitrogen...

s and enzyme

Enzyme

Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...

s often belong to low molecular symmetry

Molecular symmetry

Molecular symmetry in chemistry describes the symmetry present in molecules and the classification of molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can predict or explain many of a molecule's chemical properties, such as its dipole moment...

 point groups. The solid crystals

Crystal structure

In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...

 of the elements often belong to the space group

Space group

In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...

s and point groups with high symmetry. (Cubic harmonics representations are often listed and referenced in point group tables.) The system has at least a fixed orientation in three dimensional Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

. Therefore the coordinate system that is used in such cases is most often a Cartesian coordinate system

Cartesian coordinate system

A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

 instead of a spherical coordinate system

Spherical coordinate system

In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...

. In a Cartesian coordinate system the atomic orbital

Atomic orbital

An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...

s are often expressed as


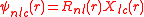
with the cubic harmonics, , as a basis set

Basis set (chemistry)

A basis set in chemistry is a set of functions used to create the molecular orbitals, which are expanded as a linear combination of such functions with the weights or coefficients to be determined. Usually these functions are atomic orbitals, in that they are centered on atoms. Otherwise, the...

. LCAO and MO

Molecular orbital theory

In chemistry, molecular orbital theory is a method for determining molecular structure in which electrons are not assigned to individual bonds between atoms, but are treated as moving under the influence of the nuclei in the whole molecule...

 calculations in computational chemistry

Computational chemistry

Computational chemistry is a branch of chemistry that uses principles of computer science to assist in solving chemical problems. It uses the results of theoretical chemistry, incorporated into efficient computer programs, to calculate the structures and properties of molecules and solids...

 or tight binding calculations in solid-state physics use cubic harmonics as an atomic orbital basis. The indices lc are denoting some kind of Cartesian representation.

Basis transformations

For the representations

Orthonormal basis

In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...

 of the spherical harmonics a spherical coordinate system is chosen with a principal axis in the z-direction. For the cubic harmonics this axis is also the most convenient choice. For states of higher angular momentum quantum number and a higher dimension of the number of possible rotations or basis transformations in Hilbert space grows and so does the number of possible orthogonal representations that can be constructed on the basis of the -dimensional spherical harmonics basis set. There is more freedom to choose a representation that fits the point group symmetry of the problem. The cubic representations that are listed in the table are a result of the transformations, which are 45^o 2D rotations and a 90^o rotation to the real axis if necessary, like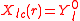


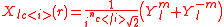
A substantial number of the spherical harmonics are listed in the Table of spherical harmonics

Table of spherical harmonics

This is a table of orthonormalized spherical harmonics that employ the Condon-Shortley phase up to degree l=10. Some of these formulas give the "Cartesian" version...

.

Computational benefits

First of all, the cubic harmonics are real functions, while spherical harmonics are complex functions. The complex numbers are two-dimensional with a real part and an imaginary part. Complex numbers offer very handsome and effective tools to tackle mathematical problems analytically but they are not very effective when they are used for numerical calculations. Skipping the imaginary part saves half the calculational effort in summations, a factor of four in multiplications and often factors of eight or even more when it comes to computations involving matrices.

The cubic harmonics often fit the symmetry of the potential or surrounding of an atom. A common surrounding of atoms in solids and chemical complexes is an octahedral surrounding with an octahedral cubic point group symmetry. The representations of the cubic harmonics often have a high symmetry and multiplicity so operations like integrations can be reduced to a limited, or irreducible, part of the domain of the function that has to be evaluated. A problem with the 48-fold octahedral O_h symmetry can be calculated much faster if one limits a calculation, like an integration, to the irreducible part of the domain of the function.

The s-orbitals

The s-orbitals only have a radial part.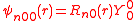

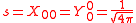
	n=1	2	3	4	5	6	7
Rn0

The p-orbitals

The three p-orbitals are atomic orbital

Atomic orbital

An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...

s with an angular momentum quantum number

Azimuthal quantum number

The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...

 ℓ = 1. The cubic harmonic expression of the p-orbitals

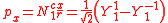
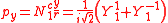
with

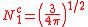
pz	px	py

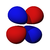
The d-orbitals

The five d-orbitals are atomic orbital

Atomic orbital

An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...

s with an angular momentum quantum number

Azimuthal quantum number

The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...

 ℓ = 2. The angular part of the d-orbitals are often expressed like


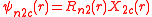
The angular part of the d-orbitals are the cubic harmonics

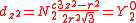
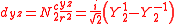
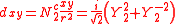
with

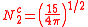
dz2	dxz	dyz	dxy	dx2-y2

The f-orbitals

The seven f-orbitals are atomic orbital

Atomic orbital

An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...

s with an angular momentum quantum number

Azimuthal quantum number

The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital...

 ℓ = 3. often expressed like


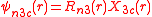
The angular part of the f-orbitals are the cubic harmonics . In many cases different linear combinations of spherical harmonics are chosen to construct a cubic f-orbital basis set.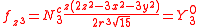

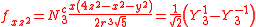
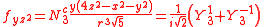
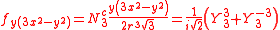
with

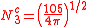
fz3	fxz2	fyz2	fxyz	fz(x2-y2)	fx(x2-3y2)	fy(3x2-y2)

See also

• Atomic orbitals
• Atomic physics
  Atomic physics
  Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
  
  
• Spherical harmonics
  Spherical harmonics
  In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
  
  
• Spherical coordinate system
  Spherical coordinate system
  In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
  
  
• Cartesian coordinate system
  Cartesian coordinate system
  A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
  
  
• Euclidean space
  Euclidean space
  In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
  
  

• Hilbert space
  Hilbert space
  The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
  
  
• Basis set (chemistry)
  Basis set (chemistry)
  A basis set in chemistry is a set of functions used to create the molecular orbitals, which are expanded as a linear combination of such functions with the weights or coefficients to be determined. Usually these functions are atomic orbitals, in that they are centered on atoms. Otherwise, the...
  
  
• Basis (linear algebra)
  Basis (linear algebra)
  In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
  
  
• Coordinate vector
  Coordinate vector
  In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
  
  
• LCAO method
  Linear combination of atomic orbitals molecular orbital method
  A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunctions...
  
  
• Tight binding method