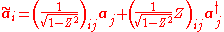Random phase approximation
Encyclopedia
The random phase approximation (RPA) is an approximation method in condensed matter physics
and in nuclear physics
. It was first introduced by David Bohm
and David Pines
as an important result in a series of seminal papers. For decades physicists had been trying to incorporate the effect of microscopic quantum mechanical interactions between electrons in the theory of matter. Bohm and Pines RPA approximation accounts for the weak screened Coulomb interaction, and RPA is commonly used for describing the dynamic linear electronic response of electron systems.
In the RPA, electron
s are assumed to respond only to the total electric potential V(r) which is the sum of the external perturbing potential Vext(r) and a screening potential Vsc(r). The external perturbing potential is assumed to oscillate at a single frequency ω, so that the model yields via a self-consistent field (SCF) method a
dynamic dielectric
function
The contribution to the dielectric function from the total electric potential is assumed to average out, so that only the potential at wave vector k contributes. This is what is meant by the random phase approximation. The resulting dielectric function, also called the Lindhard dielectric function , correctly predicts a number of properties of the electron gas, including plasmon
s .
The RPA was criticized in the late 50's for overcounting the degrees of freedom and the call for justification lead to intense work among theoretical physicists. In a seminal paper Murray Gell-Mann
and Keith Brueckner
showed that the RPA can be derived from a summation of leading-order chain Feynman diagram
s in a dense electron gas.
The consistency in these results became an important justification and motivated a very strong growth in theoretical physics in the late 50's and 60's.
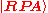 for a bosonic system can be expressed in terms of non-correlated bosonic vacuum
for a bosonic system can be expressed in terms of non-correlated bosonic vacuum 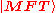 and original boson excitations
and original boson excitations 

where Z is a symmetric matrix with and
and

The normalization can be calculated by
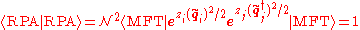
where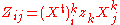 is the singular value decomposition
is the singular value decomposition
of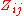 .
.
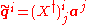

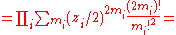

the connection between new and old excitations is given by
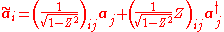
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
and in nuclear physics
Nuclear physics
Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
. It was first introduced by David Bohm
David Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
and David Pines
David Pines
David Pines is the Founding Director of the Institute for Complex Adaptive Matter and the International Institute for Complex Adaptive Matter , Distinguished Professor of Physics, UC Davis, Research Professor of Physics and Professor...
as an important result in a series of seminal papers. For decades physicists had been trying to incorporate the effect of microscopic quantum mechanical interactions between electrons in the theory of matter. Bohm and Pines RPA approximation accounts for the weak screened Coulomb interaction, and RPA is commonly used for describing the dynamic linear electronic response of electron systems.
In the RPA, electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s are assumed to respond only to the total electric potential V(r) which is the sum of the external perturbing potential Vext(r) and a screening potential Vsc(r). The external perturbing potential is assumed to oscillate at a single frequency ω, so that the model yields via a self-consistent field (SCF) method a
dynamic dielectric
Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
function
- εRPA(k, ω).
The contribution to the dielectric function from the total electric potential is assumed to average out, so that only the potential at wave vector k contributes. This is what is meant by the random phase approximation. The resulting dielectric function, also called the Lindhard dielectric function , correctly predicts a number of properties of the electron gas, including plasmon
Plasmon
In physics, a plasmon is a quantum of plasma oscillation. The plasmon is a quasiparticle resulting from the quantization of plasma oscillations just as photons and phonons are quantizations of light and mechanical vibrations, respectively...
s .
The RPA was criticized in the late 50's for overcounting the degrees of freedom and the call for justification lead to intense work among theoretical physicists. In a seminal paper Murray Gell-Mann
Murray Gell-Mann
Murray Gell-Mann is an American physicist and linguist who received the 1969 Nobel Prize in physics for his work on the theory of elementary particles...
and Keith Brueckner
Keith Brueckner
Keith Allen Brueckner is a theoretical physicist who has given important contributions in several areas of physics, including many-body theory in condensed matter physics, and laser fusion. He was born in Minneapolis on March 19, 1924. He earned a B.A. and M.A. in mathematics from the University...
showed that the RPA can be derived from a summation of leading-order chain Feynman diagram
Feynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s in a dense electron gas.
The consistency in these results became an important justification and motivated a very strong growth in theoretical physics in the late 50's and 60's.
RPA Ground State
The RPA vacuum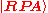 for a bosonic system can be expressed in terms of non-correlated bosonic vacuum
for a bosonic system can be expressed in terms of non-correlated bosonic vacuum 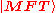 and original boson excitations
and original boson excitations 

where Z is a symmetric matrix with
 and
and
The normalization can be calculated by
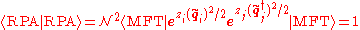
where
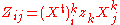 is the singular value decomposition
is the singular value decompositionSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of
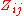 .
.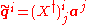

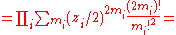

the connection between new and old excitations is given by