
Three-twist knot
Encyclopedia
In knot theory
, the three-twist knot is the twist knot
with three-half twists. It is listed as the 52 knot in the Alexander-Briggs notation, and is one of two knots with crossing number
five, the other being the cinquefoil knot
.
The three-twist knot is a prime knot
, and it is invertible
but not amphichiral
. Its Alexander polynomial
is
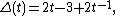
its Conway polynomial
is
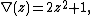
and its Jones polynomial is
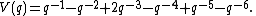
Because the Alexander polynomial is not monic, the three-twist knot is not fibered
.
The three-twist knot is a hyperbolic knot, with its complement having a volume
of approximately 2.82812.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the three-twist knot is the twist knot
Twist knot
In knot theory, a branch of mathematics, a twist knot is a knot obtained by repeatedly twisting a closed loop and then linking the ends together...
with three-half twists. It is listed as the 52 knot in the Alexander-Briggs notation, and is one of two knots with crossing number
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
five, the other being the cinquefoil knot
Cinquefoil knot
In knot theory, the cinquefoil knot, also known as Solomon's seal knot or the pentafoil knot, is one of two knots with crossing number five, the other being the three-twist knot. It is listed as the 51 knot in the Alexander-Briggs notation, and can also be described as the -torus knot...
.
The three-twist knot is a prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
, and it is invertible
Invertible knot
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant...
but not amphichiral
Amphichiral knot
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphichiral knot, also called an achiral knot or amphicheiral knot. The chirality of a knot is a knot invariant...
. Its Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
is
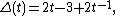
its Conway polynomial
Conway polynomial
In mathematics, Conway polynomial can refer to:* the Alexander–Conway polynomial in knot theory* the Conway polynomial...
is
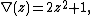
and its Jones polynomial is
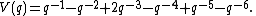
Because the Alexander polynomial is not monic, the three-twist knot is not fibered
Fibered knot
A knot or link Kin the 3-dimensional sphere S^3 is called fibered or fibred if there is a 1-parameter family F_t of Seifert surfaces for K, where the parameter t runs through the points of the unit circle S^1, such that if s is not equal to t...
.
The three-twist knot is a hyperbolic knot, with its complement having a volume
Hyperbolic volume (knot)
In the mathematical field of knot theory, the hyperbolic volume of a hyperbolic link is simply the volume of the link's complement with respect to its complete hyperbolic metric. The volume is necessarily finite. The hyperbolic volume of a non-hyperbolic knot is often defined to be zero...
of approximately 2.82812.

