
Tensor product of fields
Encyclopedia
In abstract algebra
, the theory of fields
lacks a direct product
: the direct product of two fields, considered as a ring
is never itself a field. On the other hand it is often required to 'join' two fields K and L, either in cases where K and L are given as subfields of a larger field M, or when K and L are both field extension
s of a smaller field N (for example a prime field).
The tensor product of fields is the best available construction on fields with which to discuss all the phenomena arising. As a ring, it is sometimes a field, and often a direct product of fields; it can, though, contain non-zero nilpotents (see radical of a ring
).
If K and L do not have isomorphic prime fields, or in other words they have different characteristics, they have no possibility of being common subfields of a field M. Correspondingly their tensor product will in that case be the trivial ring (collapse of the construction to nothing of interest).
. The idea behind the compositum is to make the smallest field containing two other fields. In order to formally define the compositum, we must first specify a tower of fields. Let k be a field and L and K be two extensions of k. The compositum, denoted KL is defined to be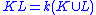 where the right hand side denotes the extension generated by K and L. Note that this assumes some field containing both K and L. Either one starts in a situation where such a common over-field is easy to identify (for example if K and L are both subfields of the complex numbers); or one proves a result that allows one to place both K and L (as isomorphic copies) in some large enough field.
where the right hand side denotes the extension generated by K and L. Note that this assumes some field containing both K and L. Either one starts in a situation where such a common over-field is easy to identify (for example if K and L are both subfields of the complex numbers); or one proves a result that allows one to place both K and L (as isomorphic copies) in some large enough field.
In many cases we can identify K.L as a vector space
tensor product
, taken over the field N that is the intersection of K and L. For example if we adjoin to the rational field Q √2 to get K, and √3 to get L, it is true that the field M obtained as K.L inside the complex numbers C is (up to
isomorphism)
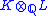
as a vector space over Q. (This type of result can be verified, in general, by using the ramification
theory of algebraic number theory
.)
Subfields K and L of M are linearly disjoint
(over a subfield N) when in this way the natural N-linear map of

to K.L is injective. Naturally enough this isn't always the case, for example when K = L. When the degrees are finite, injective is equivalent here to bijective.
A significant case in the theory of cyclotomic field
s is that for the n-th roots of unity, for n a composite number, the subfields generated by the pkth roots of unity for prime power
s dividing n are linearly disjoint for distinct p.
 . We can define the product
. We can define the product 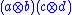 to be
to be  . This formula is multilinear over N in each variable; and so defines a ring structure on the tensor product, making
. This formula is multilinear over N in each variable; and so defines a ring structure on the tensor product, making  into a commutative N-algebra
into a commutative N-algebra
, called the tensor product of fields.
that K and L are subfields of some field M (thus getting round the caveats about constructing a compositum field). Whenever we embed K and L in such a field M, say using embeddings α of K and β of L, there results a ring homomorphism γ from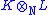 into M defined by:
into M defined by:
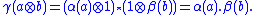
The kernel of γ will be a prime ideal
of the tensor product; and conversely any prime ideal of the tensor product will give a homomorphism of N-algebras to an integral domain (inside a field of fractions
) and so provides embeddings of K and L in some field as extensions of (a copy of) N.
In this way one can analyse the structure of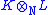 : there may in principle be a non-zero Jacobson radical
: there may in principle be a non-zero Jacobson radical
(intersection of all prime ideals) - and after taking the quotient by that we can speak of the product of all embeddings of K and L in various M, over N.
In case K and L are finite extensions of N, the situation is particularly simple, since the tensor product is of finite dimension as an N-algebra (and thus an Artinian ring
). We can then say that if R is the radical we have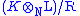 a direct product of finitely many fields. Each such field is a representative of an equivalence class of (essentially distinct) field embeddings for K and L in some extension of M.
a direct product of finitely many fields. Each such field is a representative of an equivalence class of (essentially distinct) field embeddings for K and L in some extension of M.
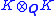 is the product of (a copy of) K, and a splitting field
is the product of (a copy of) K, and a splitting field
of
of degree 6 over Q. One can prove this by calculating the dimension of the tensor product over Q as 9, and observing that the splitting field does contain two (indeed three) copies of K, and is the compositum of two of them. That incidentally shows that R = {0} in this case.
An example leading to a non-zero nilpotent: let
with K the field of rational function
s in the indeterminate T over the finite field with p elements. (See separable polynomial
: the point here is that P is not separable). If L is the field extension K(T1/p) (the splitting field
of P) then L/K is an example of a purely inseparable field extension. In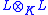 the element
the element
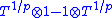
is nilpotent: by taking its pth power one gets 0 by using K-linearity.
, tensor products of fields are (implicitly, often) a basic tool. If K is an extension of Q of finite degree n,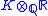 is always a product of fields isomorphic to R or C. The totally real number field
is always a product of fields isomorphic to R or C. The totally real number field
s are those for which only real fields occur: in general there are r1 real and r2 complex fields, with r1 + 2r2 = n as one sees by counting dimensions. The field factors are in 1-1 correspondence with the real embeddings, and pairs of complex conjugate embeddings, described in the classical literature.
This idea applies also to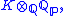 where Qp is the field of p-adic numbers
where Qp is the field of p-adic numbers
. This is a product of finite extensions of Qp, in 1-1 correspondence with the completions of K for extensions of the p-adic metric on Q.
(along lines exploited in Grothendieck's Galois theory
). It can be shown that for separable extension
s the radical is always {0}; therefore the Galois theory case is the semisimple one, of products of fields alone.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the theory of fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
lacks a direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
: the direct product of two fields, considered as a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is never itself a field. On the other hand it is often required to 'join' two fields K and L, either in cases where K and L are given as subfields of a larger field M, or when K and L are both field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
s of a smaller field N (for example a prime field).
The tensor product of fields is the best available construction on fields with which to discuss all the phenomena arising. As a ring, it is sometimes a field, and often a direct product of fields; it can, though, contain non-zero nilpotents (see radical of a ring
Radical of a ring
In ring theory, a branch of mathematics, a radical of a ring is an ideal of "bad" elements of the ring.The first example of a radical was the nilradical introduced in , based on a suggestion in . In the next few years several other radicals were discovered, of which the most important example is...
).
If K and L do not have isomorphic prime fields, or in other words they have different characteristics, they have no possibility of being common subfields of a field M. Correspondingly their tensor product will in that case be the trivial ring (collapse of the construction to nothing of interest).
Compositum of fields
Firstly, we will define the notion of the compositum of fields. This construction occurs frequently in field theoryField theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
. The idea behind the compositum is to make the smallest field containing two other fields. In order to formally define the compositum, we must first specify a tower of fields. Let k be a field and L and K be two extensions of k. The compositum, denoted KL is defined to be
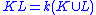 where the right hand side denotes the extension generated by K and L. Note that this assumes some field containing both K and L. Either one starts in a situation where such a common over-field is easy to identify (for example if K and L are both subfields of the complex numbers); or one proves a result that allows one to place both K and L (as isomorphic copies) in some large enough field.
where the right hand side denotes the extension generated by K and L. Note that this assumes some field containing both K and L. Either one starts in a situation where such a common over-field is easy to identify (for example if K and L are both subfields of the complex numbers); or one proves a result that allows one to place both K and L (as isomorphic copies) in some large enough field.In many cases we can identify K.L as a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
, taken over the field N that is the intersection of K and L. For example if we adjoin to the rational field Q √2 to get K, and √3 to get L, it is true that the field M obtained as K.L inside the complex numbers C is (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism)
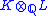
as a vector space over Q. (This type of result can be verified, in general, by using the ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
theory of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.)
Subfields K and L of M are linearly disjoint
Linearly disjoint
In mathematics, algebras A, B over a field k inside some field extension \Omega of k are said to be linearly disjoint over k if the following equivalent conditions are met:...
(over a subfield N) when in this way the natural N-linear map of

to K.L is injective. Naturally enough this isn't always the case, for example when K = L. When the degrees are finite, injective is equivalent here to bijective.
A significant case in the theory of cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
s is that for the n-th roots of unity, for n a composite number, the subfields generated by the pkth roots of unity for prime power
Prime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
s dividing n are linearly disjoint for distinct p.
The tensor product as ring
To get a general theory, we need to consider a ring structure on . We can define the product
. We can define the product 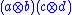 to be
to be  . This formula is multilinear over N in each variable; and so defines a ring structure on the tensor product, making
. This formula is multilinear over N in each variable; and so defines a ring structure on the tensor product, making  into a commutative N-algebra
into a commutative N-algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, called the tensor product of fields.
Analysis of the ring structure
The structure of the ring can be analysed, by considering all ways of embedding both K and L in some field extension of N. Note for this that the construction assumes the common subfield N; but does not assume a prioriA priori (statistics)
In statistics, a priori knowledge is prior knowledge about a population, rather than that estimated by recent observation. It is common in Bayesian inference to make inferences conditional upon this knowledge, and the integration of a priori knowledge is the central difference between the Bayesian...
that K and L are subfields of some field M (thus getting round the caveats about constructing a compositum field). Whenever we embed K and L in such a field M, say using embeddings α of K and β of L, there results a ring homomorphism γ from
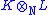 into M defined by:
into M defined by: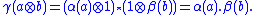
The kernel of γ will be a prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
of the tensor product; and conversely any prime ideal of the tensor product will give a homomorphism of N-algebras to an integral domain (inside a field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
) and so provides embeddings of K and L in some field as extensions of (a copy of) N.
In this way one can analyse the structure of
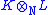 : there may in principle be a non-zero Jacobson radical
: there may in principle be a non-zero Jacobson radicalJacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
(intersection of all prime ideals) - and after taking the quotient by that we can speak of the product of all embeddings of K and L in various M, over N.
In case K and L are finite extensions of N, the situation is particularly simple, since the tensor product is of finite dimension as an N-algebra (and thus an Artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
). We can then say that if R is the radical we have
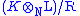 a direct product of finitely many fields. Each such field is a representative of an equivalence class of (essentially distinct) field embeddings for K and L in some extension of M.
a direct product of finitely many fields. Each such field is a representative of an equivalence class of (essentially distinct) field embeddings for K and L in some extension of M.Examples
For example, if K is generated over Q by the cube root of 2, then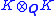 is the product of (a copy of) K, and a splitting field
is the product of (a copy of) K, and a splitting fieldSplitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of
- X3 − 2,
of degree 6 over Q. One can prove this by calculating the dimension of the tensor product over Q as 9, and observing that the splitting field does contain two (indeed three) copies of K, and is the compositum of two of them. That incidentally shows that R = {0} in this case.
An example leading to a non-zero nilpotent: let
- P(X) = Xp − T
with K the field of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s in the indeterminate T over the finite field with p elements. (See separable polynomial
Separable polynomial
In mathematics, two slightly different notions of separable polynomial are used, by different authors.According to the most common one, a polynomial P over a given field K is separable if all its roots are distinct in an algebraic closure of K, that is the number of its distinct roots is equal to...
: the point here is that P is not separable). If L is the field extension K(T1/p) (the splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of P) then L/K is an example of a purely inseparable field extension. In
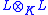 the element
the element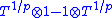
is nilpotent: by taking its pth power one gets 0 by using K-linearity.
Classical theory of real and complex embeddings
In algebraic number theoryAlgebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, tensor products of fields are (implicitly, often) a basic tool. If K is an extension of Q of finite degree n,
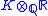 is always a product of fields isomorphic to R or C. The totally real number field
is always a product of fields isomorphic to R or C. The totally real number fieldTotally real number field
In number theory, a number field K is called totally real if for each embedding of K into the complex numbers the image lies inside the real numbers...
s are those for which only real fields occur: in general there are r1 real and r2 complex fields, with r1 + 2r2 = n as one sees by counting dimensions. The field factors are in 1-1 correspondence with the real embeddings, and pairs of complex conjugate embeddings, described in the classical literature.
This idea applies also to
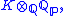 where Qp is the field of p-adic numbers
where Qp is the field of p-adic numbersP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
. This is a product of finite extensions of Qp, in 1-1 correspondence with the completions of K for extensions of the p-adic metric on Q.
Consequences for Galois theory
This gives a general picture, and indeed a way of developing Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
(along lines exploited in Grothendieck's Galois theory
Grothendieck's Galois theory
In mathematics, Grothendieck's Galois theory is a highly abstract approach to the Galois theory of fields, developed around 1960 to provide a way to study the fundamental group of algebraic topology in the setting of algebraic geometry...
). It can be shown that for separable extension
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
s the radical is always {0}; therefore the Galois theory case is the semisimple one, of products of fields alone.
See also
- Extension of scalarsExtension of scalarsIn abstract algebra, extension of scalars is a means of producing a module over a ring S from a module over another ring R, given a homomorphism f : R \to S between them...
—tensor product of a field extension and a module over that field

