
Tatyana Shaposhnikova
Encyclopedia
Tatyana Olegovna Shaposhnikova is a Russia
n mathematician
, working at Linköping University
, Sweden
. She is best known for her work in the theory of multipliers in function space
s, partial differential operators and history of mathematics
, some of which was partly done jointly with Vladimir Maz'ya. She is also a translator of both scientific and literary texts
.
. In 1973 she was awarded the Kandidat Nauk degree. From 1973 to 1990 she worked in the mathematics departments of a number of technical institutes in Leningrad
, first as an assistant and then as an associate professor. She lost her job twice because of her contacts with active dissident
s, thus having to change her employer. She immigrated in Sweden
in 1990 with her family. From July 1, 1991 she works as associate professor (universitetslektor) at the Department of Mathematics of the University of Linköping. She held a position of full professor at the Department of Mathematics of the Ohio State University
, from 2004 to 2008.
Currently she serves as a member of the European Mathematical Society
Ethics Committee
and as a member of the editorial boards of the journal Complex variable and Elliptic Equations and of the Eurasian Mathematical Journal.
for their work resulting in the first scientific
biography
of Jacques Hadamard
. On May 2010 she was awarded the Thureus prize by the Royal Society of Sciences in Uppsala
"for her outstanding contribution to the theory of partial differential equations and in particular to the theory of multipliers in function spaces".
of differentiable function
s has been the main research theme of the work of T. Shaposhnikova. She found conditions for the boundedness
of singular integrals and pseudodifferential operators acting between pairs of Sobolev space
s in 1995. In 1989 she showed that multipliers in Bessel potential spaces
are traces
of multipliers belonging to a certain class of differentiable functions with a weighted
mixed norm. A large part of her joint work with Vladimir Maz'ya on the theory of multipliers involves their analytic characterization, trace
inequalities and relations between traces and extension of multipliers, relations of Sobolev
multipliers and other function spaces, maximal subalgebras
of multiplier spaces, estimates of their essential norm and compactness
of multipliers.
of differentiable function
s on a given domain (1986, 1987). She described the structure of composition operator
s in spaces of multipliers between Sobolev space
s and gave applications of those results to semilinear elliptic systems of equations (1987). She also showed that multipliers can be naturally suited to deal with the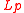
coercivity of the Neumann problem (1989). Various other applications of multipliers, for example to the problem of higher regularity in single and double layer
potential theory
for Lipschitz domain
s, to the problem of regularity at the boundary in the -theory
-theory
of elliptic boundary value problem
s and to singular integral operators in Sobolev space
s are summarized in the book .
, coauthored with V. Maz'ya, was published in 1998 jointly by the American Mathematical Society
and the London Mathematical Society
. An earlier work on the same subject was written by her jointly with E. Polishchuk (1990). Her recent activity in this field includes the paper telling three stories of scientists who were forced to answer a mathematical question under rather trying circumstances.
and edited
several mathematical
monograph
s: it is worth to note the works by and by , the book on Sobolev space
s by , and the books by and by . However, her work is not restricted only to the translation of monographs: for example she translated into Russian
a play
by Lars Gårding
, titled "Mathematics, Life and Death", published the mathematical journal
Algebra i Analiz (Алгебра и анализ).
Prof. Shaposhnikova began translating fiction while still living in Russia
. In the 1970s she translated into Russian
"The Voyage of the Dawn Treader
", "The Silver Chair
" and the "Screwtape Letters" by C. S. Lewis
. These translation
s were impossible to publish and were distributed as samizdat
: they first appeared as proper publications only in the mid 1990s, with new reprints appearing regularly.
In 2005 she began translating Swedish
children's books into Russian
. Among them are "Kerstin and I" by Astrid Lindgren
, "Mechanical Santa Claus" by Sven Nordqvist
and two books of the "Loranga" series by Barbro Lindgren.
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, working at Linköping University
Linköping University
Linköping University is a state university in Linköping, Sweden. Linköping University was granted full university status in 1975 and is now one of Sweden's larger academic institutions. Education, research and PhD training are the mission of four faculties: Arts and Sciences, Educational...
, Sweden
Sweden
Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....
. She is best known for her work in the theory of multipliers in function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
s, partial differential operators and history of mathematics
History of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
, some of which was partly done jointly with Vladimir Maz'ya. She is also a translator of both scientific and literary texts
Text (literary theory)
A text, within literary theory, is a coherent set of symbols that transmits some kind of informative message. This set of symbols is considered in terms of the informative message's content, rather than in terms of its physical form or the medium in which it is represented...
.
Academic career
T.O. Shaposhnikova graduated from Leningrad University in 1969. From 1969 to 1972 she was a graduate student at the same universityUniversity
A university is an institution of higher education and research, which grants academic degrees in a variety of subjects. A university is an organisation that provides both undergraduate education and postgraduate education...
. In 1973 she was awarded the Kandidat Nauk degree. From 1973 to 1990 she worked in the mathematics departments of a number of technical institutes in Leningrad
Leningrad
Leningrad is the former name of Saint Petersburg, Russia.Leningrad may also refer to:- Places :* Leningrad Oblast, a federal subject of Russia, around Saint Petersburg* Leningrad, Tajikistan, capital of Muminobod district in Khatlon Province...
, first as an assistant and then as an associate professor. She lost her job twice because of her contacts with active dissident
Dissident
A dissident, broadly defined, is a person who actively challenges an established doctrine, policy, or institution. When dissidents unite for a common cause they often effect a dissident movement....
s, thus having to change her employer. She immigrated in Sweden
Sweden
Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....
in 1990 with her family. From July 1, 1991 she works as associate professor (universitetslektor) at the Department of Mathematics of the University of Linköping. She held a position of full professor at the Department of Mathematics of the Ohio State University
Ohio State University
The Ohio State University, commonly referred to as Ohio State, is a public research university located in Columbus, Ohio. It was originally founded in 1870 as a land-grant university and is currently the third largest university campus in the United States...
, from 2004 to 2008.
Currently she serves as a member of the European Mathematical Society
European Mathematical Society
The European Mathematical Society is a European organization dedicated to the development of mathematics in Europe. Its members are different mathematical societies in Europe, academic institutions and individual mathematicians...
Ethics Committee
Ethics committee (disambiguation)
An ethics committee is a committee dedicated to the rights and well-being of research subjects, also known as an Institutional Review Board and may refer to:...
and as a member of the editorial boards of the journal Complex variable and Elliptic Equations and of the Eurasian Mathematical Journal.
Honors
On March 2003 Prof. Shaposhnikova and Vladimir Maz'ya were awarded the Verdaguer Prize by the French Academy of SciencesFrench Academy of Sciences
The French Academy of Sciences is a learned society, founded in 1666 by Louis XIV at the suggestion of Jean-Baptiste Colbert, to encourage and protect the spirit of French scientific research...
for their work resulting in the first scientific
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
biography
Biography
A biography is a detailed description or account of someone's life. More than a list of basic facts , biography also portrays the subject's experience of those events...
of Jacques Hadamard
Jacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
. On May 2010 she was awarded the Thureus prize by the Royal Society of Sciences in Uppsala
Royal Society of Sciences in Uppsala
The Royal Society of Sciences in Uppsala , is the oldest of the royal academies in Sweden. The society has, by royal decree of 1906, 50 Swedish fellows and 100 foreign....
"for her outstanding contribution to the theory of partial differential equations and in particular to the theory of multipliers in function spaces".
Function spaces
From 1979 on, the theory of multipliers in various spacesFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s has been the main research theme of the work of T. Shaposhnikova. She found conditions for the boundedness
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
of singular integrals and pseudodifferential operators acting between pairs of Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s in 1995. In 1989 she showed that multipliers in Bessel potential spaces
Bessel potential
In mathematics, the Bessel potential is a potential similar to the Riesz potential but with better decay properties at infinity....
are traces
Trace operator
In mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
of multipliers belonging to a certain class of differentiable functions with a weighted
Weighted space
In functional analysis, a weighted space is a space of functions under a weighted norm, which is a finite norm that involves multiplication by a particular function referred to as the weight....
mixed norm. A large part of her joint work with Vladimir Maz'ya on the theory of multipliers involves their analytic characterization, trace
Trace operator
In mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
inequalities and relations between traces and extension of multipliers, relations of Sobolev
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
multipliers and other function spaces, maximal subalgebras
Algebra (ring theory)
In mathematics, specifically in ring theory, an algebra over a commutative ring is a generalization of the concept of an algebra over a field, where the base field K is replaced by a commutative ring R....
of multiplier spaces, estimates of their essential norm and compactness
Compact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
of multipliers.
Linear and non-linear PDEs
Based on her researches on the theory of multipliers, T. Shaposhnikova gave various applications of this theory to the study of solutions to second order linear and quasilinear elliptic partial differential equations and systems of such equations: this was a consequence of the fact that, in several cases, such solutions can be considered as multipliers in certain spacesFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s on a given domain (1986, 1987). She described the structure of composition operator
Composition operator
In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the ruleC_\phi = f \circ\phiwhere f \circ\phi denotes function composition. In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman...
s in spaces of multipliers between Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s and gave applications of those results to semilinear elliptic systems of equations (1987). She also showed that multipliers can be naturally suited to deal with the
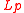
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
coercivity of the Neumann problem (1989). Various other applications of multipliers, for example to the problem of higher regularity in single and double layer
Double layer potential
In potential theory, an area of mathematics, a double layer potential is a solution of Laplace's equation corresponding to the electrostatic or magnetic potential associated to a dipole distribution on a closed surface S in three-dimensions...
potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
for Lipschitz domain
Lipschitz domain
In mathematics, a Lipschitz domain is a domain in Euclidean space whose boundary is "sufficiently regular" in the sense that it can be thought of as locally being the graph of a Lipschitz continuous function...
s, to the problem of regularity at the boundary in the
 -theory
-theoryLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of elliptic boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
s and to singular integral operators in Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s are summarized in the book .
History of mathematics
Her prize winning book on Jacques HadamardJacques Hadamard
Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...
, coauthored with V. Maz'ya, was published in 1998 jointly by the American Mathematical Society
American Mathematical Society
The American Mathematical Society is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, which it does with various publications and conferences as well as annual monetary awards and prizes to mathematicians.The society is one of the...
and the London Mathematical Society
London Mathematical Society
-See also:* American Mathematical Society* Edinburgh Mathematical Society* European Mathematical Society* List of Mathematical Societies* Council for the Mathematical Sciences* BCS-FACS Specialist Group-External links:* * *...
. An earlier work on the same subject was written by her jointly with E. Polishchuk (1990). Her recent activity in this field includes the paper telling three stories of scientists who were forced to answer a mathematical question under rather trying circumstances.
Translation and editing activity
T.O. Shaposhnikova has translatedTranslation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
and edited
Editor
The term editor may refer to:As a person who does editing:* Editor in chief, having final responsibility for a publication's operations and policies* Copy editing, making formatting changes and other improvements to text...
several mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
monograph
Monograph
A monograph is a work of writing upon a single subject, usually by a single author.It is often a scholarly essay or learned treatise, and may be released in the manner of a book or journal article. It is by definition a single document that forms a complete text in itself...
s: it is worth to note the works by and by , the book on Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s by , and the books by and by . However, her work is not restricted only to the translation of monographs: for example she translated into Russian
Russian language
Russian is a Slavic language used primarily in Russia, Belarus, Uzbekistan, Kazakhstan, Tajikistan and Kyrgyzstan. It is an unofficial but widely spoken language in Ukraine, Moldova, Latvia, Turkmenistan and Estonia and, to a lesser extent, the other countries that were once constituent republics...
a play
Play (theatre)
A play is a form of literature written by a playwright, usually consisting of scripted dialogue between characters, intended for theatrical performance rather than just reading. There are rare dramatists, notably George Bernard Shaw, who have had little preference whether their plays were performed...
by Lars Gårding
Lars Gårding
Lars Gårding is a Swedish mathematician. He has made notable contributions to the study of partial differential operators. He is a professor emeritus of mathematics at Lund University in Sweden...
, titled "Mathematics, Life and Death", published the mathematical journal
Mathematical journal
A mathematics journal is a scientific journal which publishes exclusively mathematics papers. A practical definition of the current state of mathematics, as a research field, is that it consists of theorems with proofs published in a reputable mathematics journal, and which usually have passed...
Algebra i Analiz (Алгебра и анализ).
Prof. Shaposhnikova began translating fiction while still living in Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
. In the 1970s she translated into Russian
Russian language
Russian is a Slavic language used primarily in Russia, Belarus, Uzbekistan, Kazakhstan, Tajikistan and Kyrgyzstan. It is an unofficial but widely spoken language in Ukraine, Moldova, Latvia, Turkmenistan and Estonia and, to a lesser extent, the other countries that were once constituent republics...
"The Voyage of the Dawn Treader
The Voyage of the Dawn Treader
The Voyage of the Dawn Treader is a fantasy novel for children by C. S. Lewis. Written in 1950, it was published in 1952 as the third book of The Chronicles of Narnia...
", "The Silver Chair
The Silver Chair
The Silver Chair is part of The Chronicles of Narnia, a series of seven fantasy novels written by C. S. Lewis. It was the fourth book published and is the sixth book chronologically. It is the first book published in the series in which the Pevensie children do not appear. The main characters are...
" and the "Screwtape Letters" by C. S. Lewis
C. S. Lewis
Clive Staples Lewis , commonly referred to as C. S. Lewis and known to his friends and family as "Jack", was a novelist, academic, medievalist, literary critic, essayist, lay theologian and Christian apologist from Belfast, Ireland...
. These translation
Translation
Translation is the communication of the meaning of a source-language text by means of an equivalent target-language text. Whereas interpreting undoubtedly antedates writing, translation began only after the appearance of written literature; there exist partial translations of the Sumerian Epic of...
s were impossible to publish and were distributed as samizdat
Samizdat
Samizdat was a key form of dissident activity across the Soviet bloc in which individuals reproduced censored publications by hand and passed the documents from reader to reader...
: they first appeared as proper publications only in the mid 1990s, with new reprints appearing regularly.
In 2005 she began translating Swedish
Swedish language
Swedish is a North Germanic language, spoken by approximately 10 million people, predominantly in Sweden and parts of Finland, especially along its coast and on the Åland islands. It is largely mutually intelligible with Norwegian and Danish...
children's books into Russian
Russian language
Russian is a Slavic language used primarily in Russia, Belarus, Uzbekistan, Kazakhstan, Tajikistan and Kyrgyzstan. It is an unofficial but widely spoken language in Ukraine, Moldova, Latvia, Turkmenistan and Estonia and, to a lesser extent, the other countries that were once constituent republics...
. Among them are "Kerstin and I" by Astrid Lindgren
Astrid Lindgren
Astrid Anna Emilia Lindgren , 14 November 1907 – 28 January 2002) was a Swedish author and screenwriter who is the world's 25th most translated author and has sold roughly 145 million copies worldwide...
, "Mechanical Santa Claus" by Sven Nordqvist
Sven Nordqvist
Sven Nordqvist is a Swedish writer and illustrator of children's books. He is best known for his series Pettson and Findus, about an old farmer, Pettson, and his talented cat, Findus.- Background :...
and two books of the "Loranga" series by Barbro Lindgren.
See also
- Function spaceFunction spaceIn mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
- Multiplier (operator theory)
- Partial differential equationPartial differential equationIn mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
- Potential theoryPotential theoryIn mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
- Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...

