
Table of polyhedron dihedral angles
Encyclopedia
The dihedral angle
s for the edge-transitive polyhedra are:
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
s for the edge-transitive polyhedra are:
| Picture | Name | Schläfli symbol |
Vertex/Face configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
exact dihedral angle (radians) |
approximate dihedral angle (degrees) |
|---|---|---|---|---|---|
| Platonic solid Platonic solid In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and... s (regular convex) |
|||||
 |
Tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
{3,3} | (3)3 | arccos(1/3) | 70.53° |
 |
Hexahedron Hexahedron A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex.... or Cube |
{4,3} | (4)3 | π/2 | 90° |
 |
Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
{3,4} | (3)4 | π − arccos(1/3) | 109.47° |
 |
Dodecahedron | {5,3} | (5)3 | π − arctan(2) | 116.56° |
 |
Icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
{3,5} | (3)5 | π − arccos(√5/3) | 138.19° |
| Kepler-Poinsot solid Kepler-Poinsot solid In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures.... s (regular nonconvex) |
|||||
 |
Small stellated dodecahedron | {5/2,5} | (5/2)5 | π − arctan(2) | 116.56° |
 |
Great dodecahedron | {5,5/2} | (5)5/2 | arctan(2) | 63.435° |
 |
Great stellated dodecahedron | {5/2,3} | (5/2)3 | arctan(2) | 63.435° |
 |
Great icosahedron | {3,5/2} | (3)5/2 | arcsin(2/3) | 41.810° |
| Quasiregular solids (Rectified regular Rectification (geometry) In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points... ) |
|||||
 |
Tetratetrahedron |  |
(3.3.3.3) | π − arccos(1/3) | 109.47° |
 |
Cuboctahedron Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
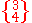 |
(3.4.3.4) | π − arccos(1/sqrt(3)) | 125.264° |
 |
Icosidodecahedron Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
 |
(3.5.3.5) |  |
142.623° |
 |
Dodecadodecahedron | 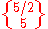 |
(5.5/2.5.5/2) | ||
 |
Great icosidodecahedron | 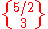 |
(3.5/2.3.5/2) | ||
| Quasiregular dual solids | |||||
 |
Dual of tetratetrahedron Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
- | V(3.3.3.3) | π − π/2 | 90° |
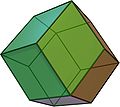 |
Rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:... (Dual of cuboctahedron) |
- | V(3.4.3.4) | π − π/3 | 120° |
 |
Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... (Dual of icosidodecahedron) |
- | V(3.5.3.5) | π − π/5 | 144° |

