
Sufficiency (statistics)
Encyclopedia
In statistics
, a sufficient statistic is a statistic
which has the property of sufficiency with respect to a statistical model
and its associated unknown parameter
, meaning that "no other statistic which can be calculated from the same sample
provides any additional information as to the value of the parameter". A statistic is sufficient for a family
of probability distribution
s if the sample from which it is calculated gives no additional information than does the statistic, as to which of those probability distributions is that of the population from which the sample was taken.
In practical terms, given a set of independent identically distributed data conditioned on an unknown parameter
of independent identically distributed data conditioned on an unknown parameter 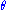 , a sufficient statistic is a function
, a sufficient statistic is a function 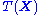 whose value contains all the information needed to compute any estimate of the parameter (e.g. a maximum likelihood
whose value contains all the information needed to compute any estimate of the parameter (e.g. a maximum likelihood
estimate). Due to the factorization theorem (see below), for a sufficient statistic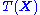 , the joint distribution
, the joint distribution
can be written as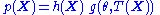 . From this factorization, it can easily be seen that the maximum likelihood estimate of
. From this factorization, it can easily be seen that the maximum likelihood estimate of 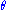 will interact with
will interact with  only through
only through 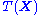 . Typically, the sufficient statistic is a simple function of the data, e.g. the sum of all the data points.
. Typically, the sufficient statistic is a simple function of the data, e.g. the sum of all the data points.
More generally, the "unknown parameter" may represent a vector of unknown quantities or may represent everything about the model that is unknown or not fully specified. In such a case, the sufficient statistic may be a set of functions, called a jointly sufficient statistic. Typically, there are as many functions as there are parameters. For example, for a Gaussian distribution with unknown mean
and variance
, the jointly sufficient statistic, from which maximum likelihood estimates of both parameters can be estimated, consists of two functions, the sum of all data points and the sum of all squared data points (or equivalently, the sample mean and sample variance).
The concept, due to Sir Ronald Fisher
, is equivalent to the statement that, conditional on the value of a sufficient statistic for a parameter, the joint probability distribution of the data does not depend on that parameter. Both the statistic and the underlying parameter can be vectors.
A related concept is that of linear sufficiency, which is weaker than sufficiency but can be applied in some cases where there is no sufficient statistic, although it is restricted to linear estimators. The Kolmogorov structure function
deals with individual finite data, the related notion there is the `algorithmic sufficient statistic.'
The concept of sufficiency has fallen out of favor in descriptive statistics
because of the strong dependence on an assumption of the distributional form (see Pitman–Koopman–Darmois theorem below), but remains very important in theoretical work.
of the data X, given the statistic T(X), does not depend on the parameter θ, i.e.
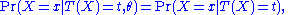
or in shorthand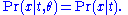
is not sufficient for the mean: even if the median of the sample is known, knowing the sample itself would provide further information about the population mean. For example, if the observations that are less than the median are only slightly less, but observations exceeding the median exceed it by a large amount, then this would have a bearing on one's inference about the population mean.
factorization theorem or factorization criterion provides a convenient characterization of a sufficient statistic. If the probability density function
is ƒθ(x), then T is sufficient for θ if and only if
functions g and h can be found such that
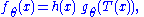
i.e. the density ƒ can be factored into a product such that one factor, h, does not depend on θ and the other factor, which does depend on θ, depends on x only through T(x).
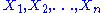 , denote a random sample from a distribution having the pdf
, denote a random sample from a distribution having the pdf
f(x, θ) for γ < θ < δ. Let Y = u(X1, X2, ..., Xn) be a statistic whose pdf is g(y; θ). Then Y = u(X1, X2, ..., Xn) is a sufficient statistic for θ if and only if, for some function H,
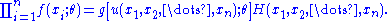
First, suppose that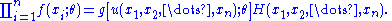
We shall make the transformation yi = ui(x1, x2, ..., xn), for i = 1, ..., n, having inverse functions xi = wi(y1, y2, ..., yn), for i = 1, ..., n, and Jacobian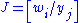 . Thus,
. Thus,
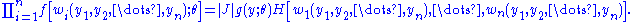
The left-hand member is the joint pdf g(y1, y2, ..., yn; θ) of Y1 = u1(X1, ..., Xn), ..., Yn = un(X1, ..., Xn). In the right-hand member, is the pdf of
is the pdf of 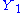 , so that
, so that  is the quotient of
is the quotient of  and
and 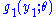 ; that is, it is the conditional pdf
; that is, it is the conditional pdf 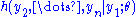 of
of  given
given 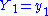 .
.
But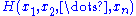 , and thus
, and thus  , was given not to depend upon
, was given not to depend upon 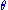 . Since
. Since 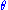 was not introduced in the transformation and accordingly not in the Jacobian
was not introduced in the transformation and accordingly not in the Jacobian 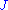 , it follows that
, it follows that 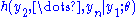 does not depend upon
does not depend upon 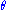 and that
and that 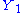 is a sufficient statistics for
is a sufficient statistics for 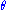 .
.
The converse is proven by taking:
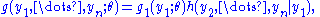
where does not depend upon
does not depend upon 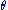 because
because  depend only upon
depend only upon  which are independent on
which are independent on  when conditioned by
when conditioned by 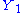 , a sufficient statistics by hypothesis. Now divide both members by the absolute value of the non-vanishing Jacobian
, a sufficient statistics by hypothesis. Now divide both members by the absolute value of the non-vanishing Jacobian 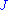 , and replace
, and replace 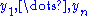 by the functions
by the functions 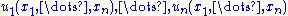 in
in  . This yields
. This yields
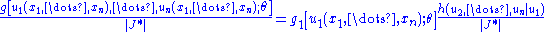
where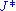 is the Jacobian with
is the Jacobian with 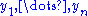 replaced by their value in terms
replaced by their value in terms  . The left-hand member is necessarily the joint pdf
. The left-hand member is necessarily the joint pdf  of
of  . Since
. Since  , and thus
, and thus  , does not depend upon
, does not depend upon  , then
, then
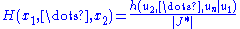
is a function that does not depend upon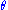 .
.
Another Proof
A simpler more illustrative proof is as follows, although it applies only in the discrete case.
We use the shorthand notation to denote the joint probability of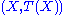 by
by 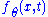 . Since
. Since 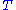 is a function of
is a function of 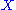 , we have
, we have 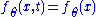 and thus:
and thus:
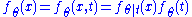
with the last equality being true by the definition of conditional probability distributions. Thus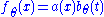 with
with 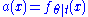 and
and 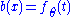 .
.
Reciprocally, if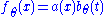 , we have
, we have
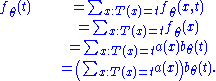
With the first equality by the definition of pdf for multiple variables, the second by the remark above, the third by hypothesis, and the fourth because the summation is not over .
.
Thus, the conditional probability distribution is: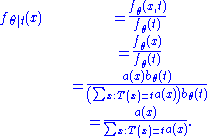
With the first equality by definition of conditional probability density, the second by the remark above, the third by the equality proven above, and the fourth by simplification. This expression does not depend on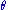 and thus
and thus 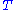 is a sufficient statistic.
is a sufficient statistic.
Intuitively, a minimal sufficient statistic most efficiently captures all possible information about the parameter θ.
A useful characterization of minimal sufficiency is that when the density fθ exists, S(X) is minimal sufficient if and only if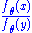 is independent of θ :
is independent of θ : S(x) = S(y)
S(x) = S(y)
This follows as a direct consequence from Fisher's factorization theorem stated above.
A case in which there is no minimal sufficient statistic was shown by Bahadur, 1957. However, under mild conditions, a minimal sufficient statistic does always exist. In particular, in Euclidean space, these conditions always hold if the random variables (associated with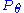 ) are all discrete or are all continuous.
) are all discrete or are all continuous.
If there exists a minimal sufficient statistic, and this is usually the case, then every complete sufficient statistic is necessarily minimal sufficient(note that this statement does not exclude the option of a pathological case in which a complete sufficient exists while there is no minimal sufficient statistic). While it is hard to find cases in which a minimal sufficient statistic does not exist, it is not so hard to find cases in which there is no complete statistic.
The collection of likelihood ratios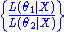 is a minimal sufficient statistic if
is a minimal sufficient statistic if 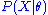 is discrete or has a density function.
is discrete or has a density function.
random variables with expected value p, then the sum T(X) = X1 + ... + Xn is a sufficient statistic for p (here 'success' corresponds to Xi = 1 and 'failure' to Xi = 0; so T is the total number of successes)
This is seen by considering the joint probability distribution:
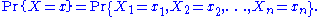
Because the observations are independent, this can be written as
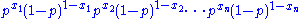
and, collecting powers of p and 1 − p, gives
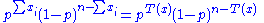
which satisfies the factorization criterion, with h(x) = 1 being just a constant.
Note the crucial feature: the unknown parameter p interacts with the data x only via the statistic T(x) = Σ xi.
on the interval [0,θ], then T(X) = max(X1, …, Xn) is sufficient for θ — the sample maximum is a sufficient statistic for the population maximum.
To see this, consider the joint probability density function
of X=(X1,…,Xn). Because the observations are independent, the pdf can be written as a product of individual densities
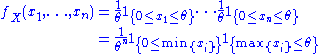
where 1{...} is the indicator function. Thus the density takes form required by the Fisher–Neyman factorization theorem, where h(x) = 1{min{xi}≥0}, and the rest of the expression is a function of only θ and T(x) = max{xi}.
In fact, the minimum-variance unbiased estimator
(MVUE) for θ is
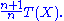
This is the sample maximum, scaled to correct for the bias
, and is MVUE by the Lehmann–Scheffé theorem
. Unscaled sample maximum T(X) is the maximum likelihood estimator for θ.
 are independent and uniformly distributed
are independent and uniformly distributed
on the interval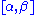 (where
(where  and
and 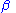 are unknown parameters), then
are unknown parameters), then 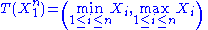 is a two-dimensional sufficient statistic for
is a two-dimensional sufficient statistic for 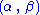 .
.
To see this, consider the joint probability density function
of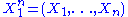 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e.
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e.
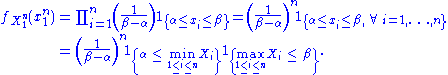
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
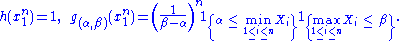
Since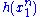 does not depend on the parameter
does not depend on the parameter 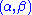 and
and 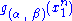 depends only on
depends only on 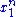 through the function
through the function 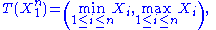
the Fisher–Neyman factorization theorem implies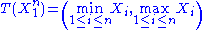 is a sufficient statistic for
is a sufficient statistic for 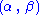 .
.
with parameter λ, then the sum T(X) = X1 + ... + Xn is a sufficient statistic for λ.
To see this, consider the joint probability distribution:
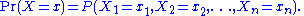
Because the observations are independent, this can be written as
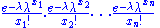
which may be written as
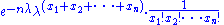
which shows that the factorization criterion is satisfied, where h(x) is the reciprocal of the product of the factorials. Note the parameter λ interacts with the data only through its sum T(X).
 are independent and normally distributed with expected value θ (a parameter) and known finite variance
are independent and normally distributed with expected value θ (a parameter) and known finite variance 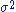 , then
, then 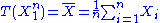 is a sufficient statistic for θ.
is a sufficient statistic for θ.
To see this, consider the joint probability density function
of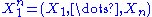 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
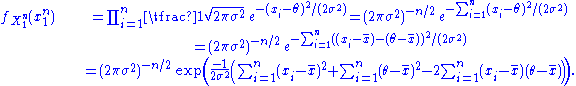
Then, since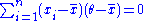 , which can be shown simply by expanding this term,
, which can be shown simply by expanding this term,
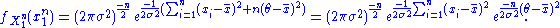
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
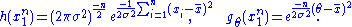
Since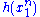 does not depend on the parameter
does not depend on the parameter 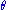 and
and 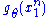 depends only on
depends only on 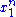 through the function
through the function 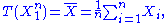
the Fisher–Neyman factorization theorem implies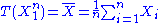 is a sufficient statistic for
is a sufficient statistic for 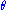 .
.
 are independent and exponentially distributed
are independent and exponentially distributed
with expected value θ (an unknown real-valued positive parameter), then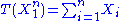 is a sufficient statistic for θ.
is a sufficient statistic for θ.
To see this, consider the joint probability density function
of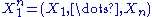 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
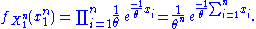
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
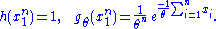
Since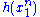 does not depend on the parameter
does not depend on the parameter 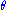 and
and 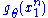 depends only on
depends only on 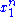 through the function
through the function 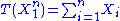
the Fisher–Neyman factorization theorem implies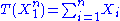 is a sufficient statistic for
is a sufficient statistic for 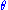 .
.
 are independent and distributed as a
are independent and distributed as a 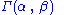 , where
, where  and
and 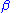 are unknown parameters of a Gamma distribution, then
are unknown parameters of a Gamma distribution, then 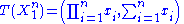 is a two-dimensional sufficient statistic for
is a two-dimensional sufficient statistic for 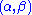 .
.
To see this, consider the joint probability density function
of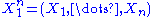 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
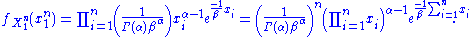
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
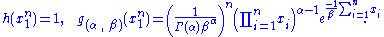
Since does not depend on the parameter
does not depend on the parameter  and
and 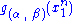 depends only on
depends only on 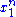 through the function
through the function 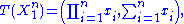
the Fisher–Neyman factorization theorem implies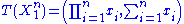 is a sufficient statistic for
is a sufficient statistic for 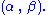
. It states that if g(X) is any kind of estimator of θ, then typically the conditional expectation of g(X) given sufficient statistic T(X) is a better estimator of θ, and is never worse. Sometimes one can very easily construct a very crude estimator g(X), and then evaluate that conditional expected value to get an estimator that is in various senses optimal.
is there a sufficient statistic whose dimension remains bounded as sample size increases. Less tersely, suppose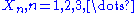 are independent identically distributed random variables whose distribution is known to be in some family of probability distributions. Only if that family is an exponential family is there a (possibly vector-valued) sufficient statistic
are independent identically distributed random variables whose distribution is known to be in some family of probability distributions. Only if that family is an exponential family is there a (possibly vector-valued) sufficient statistic 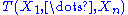 whose number of scalar components does not increase as the sample size n increases.
whose number of scalar components does not increase as the sample size n increases.
This theorem shows that sufficiency (or rather, the existence of a scalar or vector-valued of bounded dimension sufficient statistic) sharply restricts the possible forms of the distribution.
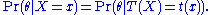
It turns out that this "Bayesian sufficiency" is a consequence of the formulation above, however they are not directly equivalent in the infinite-dimensional case. A range of theoretical results for sufficiency in a Bayesian context is available.
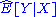 . Then a linear statistic T(x) is linear sufficient if
. Then a linear statistic T(x) is linear sufficient if
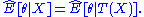
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a sufficient statistic is a statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
which has the property of sufficiency with respect to a statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
and its associated unknown parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
, meaning that "no other statistic which can be calculated from the same sample
Sample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
provides any additional information as to the value of the parameter". A statistic is sufficient for a family
Parametric family
In mathematics and its applications, a parametric family or a parameterized family is a family of objects whose definitions depend on a set of parameters....
of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s if the sample from which it is calculated gives no additional information than does the statistic, as to which of those probability distributions is that of the population from which the sample was taken.
In practical terms, given a set
 of independent identically distributed data conditioned on an unknown parameter
of independent identically distributed data conditioned on an unknown parameter 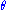 , a sufficient statistic is a function
, a sufficient statistic is a function 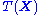 whose value contains all the information needed to compute any estimate of the parameter (e.g. a maximum likelihood
whose value contains all the information needed to compute any estimate of the parameter (e.g. a maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate). Due to the factorization theorem (see below), for a sufficient statistic
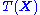 , the joint distribution
, the joint distributionJoint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
can be written as
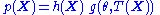 . From this factorization, it can easily be seen that the maximum likelihood estimate of
. From this factorization, it can easily be seen that the maximum likelihood estimate of 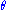 will interact with
will interact with  only through
only through 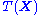 . Typically, the sufficient statistic is a simple function of the data, e.g. the sum of all the data points.
. Typically, the sufficient statistic is a simple function of the data, e.g. the sum of all the data points.More generally, the "unknown parameter" may represent a vector of unknown quantities or may represent everything about the model that is unknown or not fully specified. In such a case, the sufficient statistic may be a set of functions, called a jointly sufficient statistic. Typically, there are as many functions as there are parameters. For example, for a Gaussian distribution with unknown mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, the jointly sufficient statistic, from which maximum likelihood estimates of both parameters can be estimated, consists of two functions, the sum of all data points and the sum of all squared data points (or equivalently, the sample mean and sample variance).
The concept, due to Sir Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
, is equivalent to the statement that, conditional on the value of a sufficient statistic for a parameter, the joint probability distribution of the data does not depend on that parameter. Both the statistic and the underlying parameter can be vectors.
A related concept is that of linear sufficiency, which is weaker than sufficiency but can be applied in some cases where there is no sufficient statistic, although it is restricted to linear estimators. The Kolmogorov structure function
Kolmogorov structure function
In 1974 Kolmogorov proposed a non-probabilistic approach to statistics and model selection. Let each data be a finite binary string and models be finite sets of binary strings...
deals with individual finite data, the related notion there is the `algorithmic sufficient statistic.'
The concept of sufficiency has fallen out of favor in descriptive statistics
Descriptive statistics
Descriptive statistics quantitatively describe the main features of a collection of data. Descriptive statistics are distinguished from inferential statistics , in that descriptive statistics aim to summarize a data set, rather than use the data to learn about the population that the data are...
because of the strong dependence on an assumption of the distributional form (see Pitman–Koopman–Darmois theorem below), but remains very important in theoretical work.
Mathematical definition
A statistic T(X) is sufficient for underlying parameter θ precisely if the conditional probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the data X, given the statistic T(X), does not depend on the parameter θ, i.e.
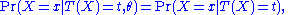
or in shorthand
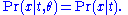
Example
As an example, the sample mean is sufficient for the mean (μ) of a normal distribution with known variance. Once the sample mean is known, no further information about μ can be obtained from the sample itself. On the other hand, the medianMedian
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
is not sufficient for the mean: even if the median of the sample is known, knowing the sample itself would provide further information about the population mean. For example, if the observations that are less than the median are only slightly less, but observations exceeding the median exceed it by a large amount, then this would have a bearing on one's inference about the population mean.
Fisher–Neyman factorization theorem
Fisher'sRonald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
factorization theorem or factorization criterion provides a convenient characterization of a sufficient statistic. If the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is ƒθ(x), then T is sufficient for θ if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
functions g and h can be found such that
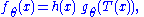
i.e. the density ƒ can be factored into a product such that one factor, h, does not depend on θ and the other factor, which does depend on θ, depends on x only through T(x).
Likelihood principle interpretation
An implication of the theorem is that when using likelihood-based inference, two sets of data yielding the same value for the sufficient statistic T(X) will always yield the same inferences about θ. By the factorization criterion, the likelihood's dependence on θ is only in conjunction with T(X). As this is the same in both cases, the dependence on θ will be the same as well, leading to identical inferences.Proof
Due to Hogg and Craig. Let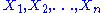 , denote a random sample from a distribution having the pdf
, denote a random sample from a distribution having the pdfProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
f(x, θ) for γ < θ < δ. Let Y = u(X1, X2, ..., Xn) be a statistic whose pdf is g(y; θ). Then Y = u(X1, X2, ..., Xn) is a sufficient statistic for θ if and only if, for some function H,
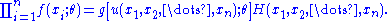
First, suppose that
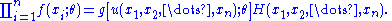
We shall make the transformation yi = ui(x1, x2, ..., xn), for i = 1, ..., n, having inverse functions xi = wi(y1, y2, ..., yn), for i = 1, ..., n, and Jacobian
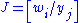 . Thus,
. Thus,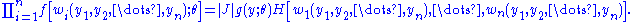
The left-hand member is the joint pdf g(y1, y2, ..., yn; θ) of Y1 = u1(X1, ..., Xn), ..., Yn = un(X1, ..., Xn). In the right-hand member,
 is the pdf of
is the pdf of 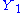 , so that
, so that  is the quotient of
is the quotient of  and
and 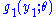 ; that is, it is the conditional pdf
; that is, it is the conditional pdf 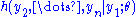 of
of  given
given 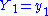 .
.But
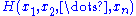 , and thus
, and thus  , was given not to depend upon
, was given not to depend upon 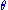 . Since
. Since 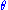 was not introduced in the transformation and accordingly not in the Jacobian
was not introduced in the transformation and accordingly not in the Jacobian 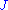 , it follows that
, it follows that 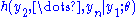 does not depend upon
does not depend upon 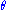 and that
and that 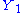 is a sufficient statistics for
is a sufficient statistics for 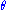 .
.The converse is proven by taking:
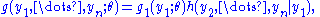
where
 does not depend upon
does not depend upon 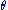 because
because  depend only upon
depend only upon  which are independent on
which are independent on  when conditioned by
when conditioned by 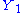 , a sufficient statistics by hypothesis. Now divide both members by the absolute value of the non-vanishing Jacobian
, a sufficient statistics by hypothesis. Now divide both members by the absolute value of the non-vanishing Jacobian 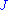 , and replace
, and replace 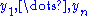 by the functions
by the functions 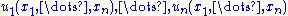 in
in  . This yields
. This yields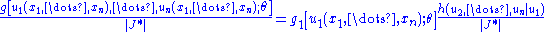
where
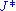 is the Jacobian with
is the Jacobian with 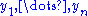 replaced by their value in terms
replaced by their value in terms  . The left-hand member is necessarily the joint pdf
. The left-hand member is necessarily the joint pdf  of
of  . Since
. Since  , and thus
, and thus  , does not depend upon
, does not depend upon 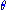 , then
, then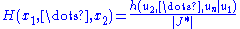
is a function that does not depend upon
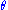 .
.Another Proof
A simpler more illustrative proof is as follows, although it applies only in the discrete case.
We use the shorthand notation to denote the joint probability of
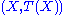 by
by 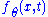 . Since
. Since 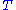 is a function of
is a function of 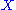 , we have
, we have 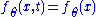 and thus:
and thus: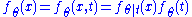
with the last equality being true by the definition of conditional probability distributions. Thus
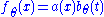 with
with 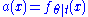 and
and 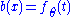 .
.Reciprocally, if
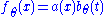 , we have
, we have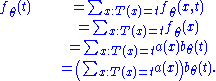
With the first equality by the definition of pdf for multiple variables, the second by the remark above, the third by hypothesis, and the fourth because the summation is not over
 .
.Thus, the conditional probability distribution is:
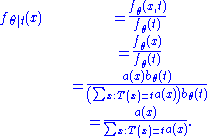
With the first equality by definition of conditional probability density, the second by the remark above, the third by the equality proven above, and the fourth by simplification. This expression does not depend on
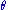 and thus
and thus 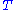 is a sufficient statistic.
is a sufficient statistic.Minimal sufficiency
A sufficient statistic is minimal sufficient if it can be represented as a function of any other sufficient statistic. In other words, S(X) is minimal sufficient if and only if- S(X) is sufficient, and
- if T(X) is sufficient, then there exists a function f such that S(X) = f(T(X)).
Intuitively, a minimal sufficient statistic most efficiently captures all possible information about the parameter θ.
A useful characterization of minimal sufficiency is that when the density fθ exists, S(X) is minimal sufficient if and only if
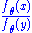 is independent of θ :
is independent of θ : S(x) = S(y)
S(x) = S(y)This follows as a direct consequence from Fisher's factorization theorem stated above.
A case in which there is no minimal sufficient statistic was shown by Bahadur, 1957. However, under mild conditions, a minimal sufficient statistic does always exist. In particular, in Euclidean space, these conditions always hold if the random variables (associated with
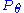 ) are all discrete or are all continuous.
) are all discrete or are all continuous.If there exists a minimal sufficient statistic, and this is usually the case, then every complete sufficient statistic is necessarily minimal sufficient(note that this statement does not exclude the option of a pathological case in which a complete sufficient exists while there is no minimal sufficient statistic). While it is hard to find cases in which a minimal sufficient statistic does not exist, it is not so hard to find cases in which there is no complete statistic.
The collection of likelihood ratios
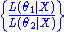 is a minimal sufficient statistic if
is a minimal sufficient statistic if 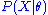 is discrete or has a density function.
is discrete or has a density function.Bernoulli distribution
If X1, ...., Xn are independent Bernoulli-distributedBernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
random variables with expected value p, then the sum T(X) = X1 + ... + Xn is a sufficient statistic for p (here 'success' corresponds to Xi = 1 and 'failure' to Xi = 0; so T is the total number of successes)
This is seen by considering the joint probability distribution:
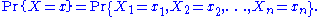
Because the observations are independent, this can be written as
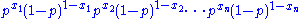
and, collecting powers of p and 1 − p, gives
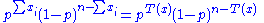
which satisfies the factorization criterion, with h(x) = 1 being just a constant.
Note the crucial feature: the unknown parameter p interacts with the data x only via the statistic T(x) = Σ xi.
Uniform distribution
If X1, ...., Xn are independent and uniformly distributedUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on the interval [0,θ], then T(X) = max(X1, …, Xn) is sufficient for θ — the sample maximum is a sufficient statistic for the population maximum.
To see this, consider the joint probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of X=(X1,…,Xn). Because the observations are independent, the pdf can be written as a product of individual densities
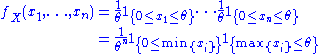
where 1{...} is the indicator function. Thus the density takes form required by the Fisher–Neyman factorization theorem, where h(x) = 1{min{xi}≥0}, and the rest of the expression is a function of only θ and T(x) = max{xi}.
In fact, the minimum-variance unbiased estimator
Minimum-variance unbiased estimator
In statistics a uniformly minimum-variance unbiased estimator or minimum-variance unbiased estimator is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.The question of determining the UMVUE, if one exists, for a particular...
(MVUE) for θ is
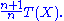
This is the sample maximum, scaled to correct for the bias
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
, and is MVUE by the Lehmann–Scheffé theorem
Lehmann–Scheffé theorem
In statistics, the Lehmann–Scheffé theorem is prominent in mathematical statistics, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation...
. Unscaled sample maximum T(X) is the maximum likelihood estimator for θ.
Uniform distribution (with two parameters)
If are independent and uniformly distributed
are independent and uniformly distributedUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on the interval
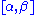 (where
(where  and
and 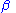 are unknown parameters), then
are unknown parameters), then 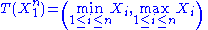 is a two-dimensional sufficient statistic for
is a two-dimensional sufficient statistic for 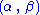 .
.To see this, consider the joint probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of
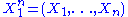 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e.
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e.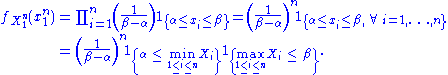
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
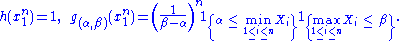
Since
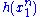 does not depend on the parameter
does not depend on the parameter 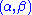 and
and 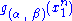 depends only on
depends only on 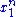 through the function
through the function 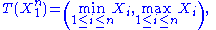
the Fisher–Neyman factorization theorem implies
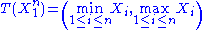 is a sufficient statistic for
is a sufficient statistic for 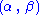 .
.Poisson distribution
If X1, ...., Xn are independent and have a Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with parameter λ, then the sum T(X) = X1 + ... + Xn is a sufficient statistic for λ.
To see this, consider the joint probability distribution:
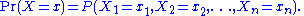
Because the observations are independent, this can be written as
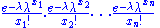
which may be written as
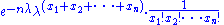
which shows that the factorization criterion is satisfied, where h(x) is the reciprocal of the product of the factorials. Note the parameter λ interacts with the data only through its sum T(X).
Normal distribution
If are independent and normally distributed with expected value θ (a parameter) and known finite variance
are independent and normally distributed with expected value θ (a parameter) and known finite variance 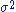 , then
, then 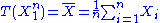 is a sufficient statistic for θ.
is a sufficient statistic for θ.To see this, consider the joint probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of
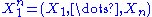 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -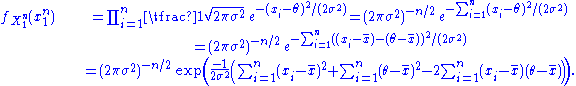
Then, since
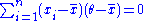 , which can be shown simply by expanding this term,
, which can be shown simply by expanding this term,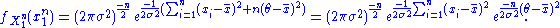
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
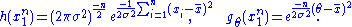
Since
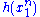 does not depend on the parameter
does not depend on the parameter 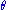 and
and 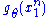 depends only on
depends only on 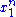 through the function
through the function 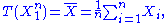
the Fisher–Neyman factorization theorem implies
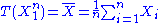 is a sufficient statistic for
is a sufficient statistic for 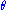 .
.Exponential distribution
If are independent and exponentially distributed
are independent and exponentially distributedExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
with expected value θ (an unknown real-valued positive parameter), then
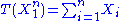 is a sufficient statistic for θ.
is a sufficient statistic for θ.To see this, consider the joint probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of
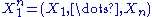 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -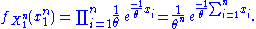
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
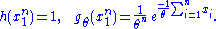
Since
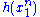 does not depend on the parameter
does not depend on the parameter 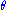 and
and 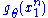 depends only on
depends only on 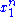 through the function
through the function 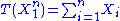
the Fisher–Neyman factorization theorem implies
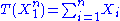 is a sufficient statistic for
is a sufficient statistic for 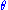 .
.Gamma distribution
If are independent and distributed as a
are independent and distributed as a 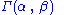 , where
, where  and
and 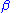 are unknown parameters of a Gamma distribution, then
are unknown parameters of a Gamma distribution, then 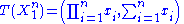 is a two-dimensional sufficient statistic for
is a two-dimensional sufficient statistic for 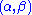 .
.To see this, consider the joint probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of
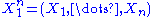 . Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -
. Because the observations are independent, the pdf can be written as a product of individual densities, i.e. -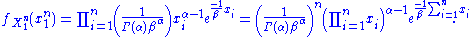
The joint density of the sample takes the form required by the Fisher–Neyman factorization theorem, by letting
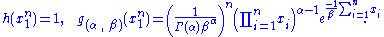
Since
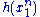 does not depend on the parameter
does not depend on the parameter 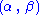 and
and 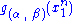 depends only on
depends only on 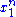 through the function
through the function 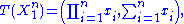
the Fisher–Neyman factorization theorem implies
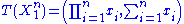 is a sufficient statistic for
is a sufficient statistic for 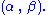
Rao–Blackwell theorem
Sufficiency finds a useful application in the Rao–Blackwell theoremRao–Blackwell theorem
In statistics, the Rao–Blackwell theorem, sometimes referred to as the Rao–Blackwell–Kolmogorov theorem, is a result which characterizes the transformation of an arbitrarily crude estimator into an estimator that is optimal by the mean-squared-error criterion or any of a variety of similar...
. It states that if g(X) is any kind of estimator of θ, then typically the conditional expectation of g(X) given sufficient statistic T(X) is a better estimator of θ, and is never worse. Sometimes one can very easily construct a very crude estimator g(X), and then evaluate that conditional expected value to get an estimator that is in various senses optimal.
Exponential family
According to the Pitman–Koopman–Darmois theorem, among families of probability distributions whose domain does not vary with the parameter being estimated, only in exponential familiesExponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
is there a sufficient statistic whose dimension remains bounded as sample size increases. Less tersely, suppose
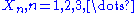 are independent identically distributed random variables whose distribution is known to be in some family of probability distributions. Only if that family is an exponential family is there a (possibly vector-valued) sufficient statistic
are independent identically distributed random variables whose distribution is known to be in some family of probability distributions. Only if that family is an exponential family is there a (possibly vector-valued) sufficient statistic 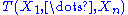 whose number of scalar components does not increase as the sample size n increases.
whose number of scalar components does not increase as the sample size n increases.This theorem shows that sufficiency (or rather, the existence of a scalar or vector-valued of bounded dimension sufficient statistic) sharply restricts the possible forms of the distribution.
Bayesian sufficiency
An alternative formulation of the condition that a statistic be sufficient, set in a Bayesian context, involves the posterior distributions obtained by using the full data-set and by using only a statistic. Thus the requirement is that, for almost every x,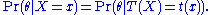
It turns out that this "Bayesian sufficiency" is a consequence of the formulation above, however they are not directly equivalent in the infinite-dimensional case. A range of theoretical results for sufficiency in a Bayesian context is available.
Linear sufficiency
A concept called "linear sufficiency" can be formulated in a Bayesian context, and more generally. First define the best linear predictor of a vector Y based on X as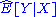 . Then a linear statistic T(x) is linear sufficient if
. Then a linear statistic T(x) is linear sufficient if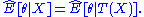
See also
- CompletenessCompleteness (statistics)In statistics, completeness is a property of a statistic in relation to a model for a set of observed data. In essence, it is a condition which ensures that the parameters of the probability distribution representing the model can all be estimated on the basis of the statistic: it ensures that the...
of a statistic - Basu's theoremBasu's theoremIn statistics, Basu's theorem states that any boundedly complete sufficient statistic is independent of any ancillary statistic. This is a 1955 result of Debabrata Basu....
on independence of complete sufficient and ancillary statistics - Lehmann–Scheffé theoremLehmann–Scheffé theoremIn statistics, the Lehmann–Scheffé theorem is prominent in mathematical statistics, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation...
: a complete sufficient estimator is the best estimator of its expectation - Rao–Blackwell theoremRao–Blackwell theoremIn statistics, the Rao–Blackwell theorem, sometimes referred to as the Rao–Blackwell–Kolmogorov theorem, is a result which characterizes the transformation of an arbitrarily crude estimator into an estimator that is optimal by the mean-squared-error criterion or any of a variety of similar...
- Sufficient dimension reductionSufficient dimension reductionIn statistics, sufficient dimension reduction is a paradigm for analyzing data that combines the ideas of dimension reduction with the concept of sufficiency.Dimension reduction has long been a primary goal of regression analysis...
- Ancillary statisticAncillary statisticIn statistics, an ancillary statistic is a statistic whose sampling distribution does not depend on which of the probability distributions among those being considered is the distribution of the statistical population from which the data were taken...

