
Statistical model
Encyclopedia
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but stochastic
ally related. In mathematical terms, a statistical model is frequently thought of as a pair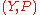 where
where  is the set of possible observations and
is the set of possible observations and 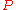 the set of possible probability distributions on
the set of possible probability distributions on  . It is assumed that there is a distinct element of
. It is assumed that there is a distinct element of 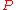 which generates the observed data. Statistical inference
which generates the observed data. Statistical inference
enables us to make statements about which element(s) of this set are likely to be the true one.
Most statistical tests can be described in the form of a statistical model. For example, the Student's t-test
for comparing the means of two groups can be formulated as seeing if an estimated parameter
in the model is different from 0. Another similarity between tests and models is that there are assumptions involved. Error is assumed to be normally distributed in most models.
 , is a collection of probability distribution functions
, is a collection of probability distribution functions
or probability density function
s (collectively referred to as distributions for brevity). A parametric model
is a collection of distributions, each of which is indexed by a unique finite-dimensional parameter: , where
, where  is a parameter and
is a parameter and 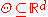 is the feasible region of parameters, which is a subset of d-dimensional Euclidean space
is the feasible region of parameters, which is a subset of d-dimensional Euclidean space
. A statistical model may be used to describe the set of distributions from which one assumes that a particular data set is sampled. For example, if one assumes that data arise from a univariate Gaussian distribution, then one has assumed a Gaussian model: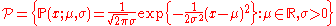 .
.
A non-parametric model is a set of probability distributions with infinite dimensional parameters, and might be written as . A semi-parametric model also has infinite dimensional parameters, but is not dense in the space of distributions. For example, a mixture of Gaussians with one Gaussian at each data point is dense is the space of distributions. Formally, if d is the dimension of the parameter, and n is the number of samples, if
. A semi-parametric model also has infinite dimensional parameters, but is not dense in the space of distributions. For example, a mixture of Gaussians with one Gaussian at each data point is dense is the space of distributions. Formally, if d is the dimension of the parameter, and n is the number of samples, if  as
as  and
and 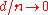 as
as  , then the model is semi-parametric.
, then the model is semi-parametric.
or a confirmatory data analysis. In an exploratory analysis, you formulate all models you can think of, and see which describes your data best. In a confirmatory analysis you test which of your models you have described before the data was collected fits the data best, or test if your only model fits the data. In linear regression analysis you can compare the amount of variance explained by the independent variables, R2, across the different models. In general, you can compare models that are nested by using a Likelihood-ratio test
. Nested models are models that can be obtained by restricting a parameter in a more complex model to be zero.
lengthi = b0 + b1agei + εi, where b0 is the intercept, b1 is a parameter that age is multiplied by to get a prediction of length, ε is the error term, and i is the subject. This means that length starts at some value, there is a minimum length when someone is born, and it is predicted by age to some amount. This prediction is not perfect as error is included in the model. This error contains variance that stems from sex and other variables. When sex is included in the model, the error term will become smaller, as you will have a better idea of the chance that a particular 16-year-old is 6 feet tall when you know this 16-year-old is a girl. The model would become lengthi = b0 + b1agei + b2sexi + εi, where the variable sex is dichotomous. This model would presumably have a higher R2. The first model is nested in the second model: the first model is obtained from the second when b2 is restricted to zero.
(restricted to continuous dependent variables), the generalized linear model
(for example, logistic regression
), the multilevel model
, and the structural equation model.
Stochastic
Stochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
ally related. In mathematical terms, a statistical model is frequently thought of as a pair
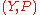 where
where  is the set of possible observations and
is the set of possible observations and 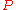 the set of possible probability distributions on
the set of possible probability distributions on  . It is assumed that there is a distinct element of
. It is assumed that there is a distinct element of 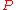 which generates the observed data. Statistical inference
which generates the observed data. Statistical inferenceStatistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
enables us to make statements about which element(s) of this set are likely to be the true one.
Most statistical tests can be described in the form of a statistical model. For example, the Student's t-test
Student's t-test
A t-test is any statistical hypothesis test in which the test statistic follows a Student's t distribution if the null hypothesis is supported. It is most commonly applied when the test statistic would follow a normal distribution if the value of a scaling term in the test statistic were known...
for comparing the means of two groups can be formulated as seeing if an estimated parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
in the model is different from 0. Another similarity between tests and models is that there are assumptions involved. Error is assumed to be normally distributed in most models.
Formal definition
A Statistical model, , is a collection of probability distribution functions
, is a collection of probability distribution functionsCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
or probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s (collectively referred to as distributions for brevity). A parametric model
Parametric model
In statistics, a parametric model or parametric family or finite-dimensional model is a family of distributions that can be described using a finite number of parameters...
is a collection of distributions, each of which is indexed by a unique finite-dimensional parameter:
 , where
, where  is a parameter and
is a parameter and 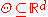 is the feasible region of parameters, which is a subset of d-dimensional Euclidean space
is the feasible region of parameters, which is a subset of d-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. A statistical model may be used to describe the set of distributions from which one assumes that a particular data set is sampled. For example, if one assumes that data arise from a univariate Gaussian distribution, then one has assumed a Gaussian model:
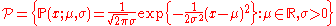 .
.A non-parametric model is a set of probability distributions with infinite dimensional parameters, and might be written as
 . A semi-parametric model also has infinite dimensional parameters, but is not dense in the space of distributions. For example, a mixture of Gaussians with one Gaussian at each data point is dense is the space of distributions. Formally, if d is the dimension of the parameter, and n is the number of samples, if
. A semi-parametric model also has infinite dimensional parameters, but is not dense in the space of distributions. For example, a mixture of Gaussians with one Gaussian at each data point is dense is the space of distributions. Formally, if d is the dimension of the parameter, and n is the number of samples, if  as
as  and
and 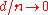 as
as  , then the model is semi-parametric.
, then the model is semi-parametric.Model comparison
Models can be compared to each other. This can either be done when you have done an exploratory data analysisExploratory data analysis
In statistics, exploratory data analysis is an approach to analysing data sets to summarize their main characteristics in easy-to-understand form, often with visual graphs, without using a statistical model or having formulated a hypothesis...
or a confirmatory data analysis. In an exploratory analysis, you formulate all models you can think of, and see which describes your data best. In a confirmatory analysis you test which of your models you have described before the data was collected fits the data best, or test if your only model fits the data. In linear regression analysis you can compare the amount of variance explained by the independent variables, R2, across the different models. In general, you can compare models that are nested by using a Likelihood-ratio test
Likelihood-ratio test
In statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...
. Nested models are models that can be obtained by restricting a parameter in a more complex model to be zero.
An example
Length and age are probabilistically distributed over humans. They are stochastically related, when you know that a person is of age 7, this influences the chance of this person being 6 feet tall. You could formalize this relationship in a linear regression model of the following form:lengthi = b0 + b1agei + εi, where b0 is the intercept, b1 is a parameter that age is multiplied by to get a prediction of length, ε is the error term, and i is the subject. This means that length starts at some value, there is a minimum length when someone is born, and it is predicted by age to some amount. This prediction is not perfect as error is included in the model. This error contains variance that stems from sex and other variables. When sex is included in the model, the error term will become smaller, as you will have a better idea of the chance that a particular 16-year-old is 6 feet tall when you know this 16-year-old is a girl. The model would become lengthi = b0 + b1agei + b2sexi + εi, where the variable sex is dichotomous. This model would presumably have a higher R2. The first model is nested in the second model: the first model is obtained from the second when b2 is restricted to zero.
Classification
According to the number of the endogenous variables and the number of equations, models can be classified as complete models (the number of equations equals to the number of endogenous variables) and incomplete models. Some other statistical models are the general linear modelGeneral linear model
The general linear model is a statistical linear model.It may be written aswhere Y is a matrix with series of multivariate measurements, X is a matrix that might be a design matrix, B is a matrix containing parameters that are usually to be estimated and U is a matrix containing errors or...
(restricted to continuous dependent variables), the generalized linear model
Generalized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
(for example, logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
), the multilevel model
Multilevel model
Multilevel models are statistical models of parameters that vary at more than one level...
, and the structural equation model.
See also
- A/B testingA/B testingA/B testing, split testing or bucket testing is a method of marketing testing by which a baseline control sample is compared to a variety of single-variable test samples in order to improve response rates...
- Mathematical diagramMathematical diagramMathematical diagrams are diagrams in the field of mathematics, and diagrams using mathematics such as charts and graphs, that are mainly designed to convey mathematical relationships, for example, comparisons over time.- Argand diagram :...
- Regression analysisRegression analysisIn statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...

