Stratifold
Encyclopedia
In differential topology
, a branch of mathematics
, a stratifold is a generalization of a differentiable manifold
where certain kinds of singularities
are allowed. More specifically a stratifold is stratified into differentiable manifolds of (possibly) different dimensions. Stratifolds can be used to construct new homology theories. For example, they provide a new geometric model for ordinary homology. The concept of stratifolds was invented by Matthias Kreck
. The basic idea is similar to that of a topologically stratified space
, but adapted to differential topology
.
such that a function is in C if it is locally in C and 
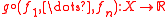is in C for 
smooth and 
. A simple example takes for X a smooth manifold and for C just the smooth functions.
For a general differential space (X, C) and a point x in X we can define as in the case of manifolds a tangent space
as the vector space
of all derivations
of function germs
at x. Define strata
has dimension i
. For an n-dimensional manifold M we have that 
and all other strata are empty. We are now ready for the definition of a stratifold, where more than one stratum may be non-empty:
A k-dimensional stratifold is a differential space (S, C), where S is a locally compact Hausdorff space
with countable base of topology. All skeleta should be closed. In addition we assume:
A n-dimensional stratifold is called oriented if its (n − 1)-stratum is empty and its top stratum is oriented. One can also define stratifolds with boundary, the so-called c-stratifolds. One defines them as a pair
of topological spaces such that 
is an n-dimensional stratifold and 
is an (n − 1)-dimensional stratifold, together with an equivalence class of collars.
An important subclass of stratifolds are the regular stratifolds, which can be roughly characterized as looking locally around a point in the i-stratum like the i-stratum times a (n − i)-dimensional stratifold. This is a condition which is fulfilled in most stratifold one usually encounters.
over a manifold M. We define a continuous function from S to the reals to be in C iff
it is smooth on M × (0, 1) and it is locally constant around the cone point. The last condition is automatic by point 2 in the definition of a stratifold. We can substitute M by a stratifold S in this construction. The cone is oriented if and only if S is oriented and not zero-dimensional. If we consider the (closed) cone with bottom, we get a stratifold with boundary S.
Other examples for stratifolds are one-point compactifications and suspensions of manifolds, (real) algebraic varieties with only isolated singularities and (finite) simplicial complexes.
from two oriented compact k-dimensional stratifolds into a space X bordant
if there exists an oriented (k + 1)-dimensional compact stratifold T with boundary S + (−S' ) such that the map to X extends to T. The set of equivalence classes of such maps 
is denoted by 
. The sets have actually the structure of abelian groups with disjoint union as addition. One can develop enough differential topology
of stratifolds to show that these define a homology theory
. Clearly,
for k > 0 since every oriented stratifold S is the boundary of its cone, which is oriented if dim(S) > 0. One can show that 
. Hence, by the Eilenberg–Steenrod uniqueness theorem, 
for every space X homotopy-equivalent to a CW-complex, where H denotes singular homology
. It should be noted, however, that for other spaces these two homology theories need not be isomorphic (an example is the one-point compactification of the surface of infinite genus).
There is also a simple way to define equivariant homology with the help of stratifolds. Let G be a compact Lie group
. We can then define a bordism theory of stratifolds mapping into a space X with a G-action just as above, only that we require all stratifolds to be equipped with an orientation-preserving free G-action and all maps to be G-equivariant. Denote by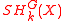
the bordism classes. One can prove 
for every X homotopy equivalent to a CW-complex.
is a ring homomorphism from a bordism ring into another ring. For example the Euler characteristic
defines a ring homomorphism
from the unoriented bordism ring and the signature
defines a ring homomorphism
from the oriented bordism ring. Here t has in the first case degree 1 and in the second case degree 4, since only manifolds in dimensions divisible by 4 can have non-zero signature. The left hand sides of these homomorphisms are homology theories evaluated at a point. With the help of stratifolds it is possible to construct homology theories such that the right hand sides are these homology theories evaluated at a point, the Euler homology and the Hirzebruch homology respectively.
of manifolds with oriented normal bundle. Then one can define an umkehr map 
. One possibility is to use stratifolds: represent a class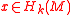 
by a stratifold 
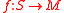. Then make ƒ transversal to N. The intersection of S and N defines a new stratifold S' with a map to N, which represents a class in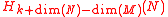 
. It is possible to repeat this construction in the context of an embedding of Hilbert manifold
s of finite codimension, which can be used in string topology
.
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a stratifold is a generalization of a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
where certain kinds of singularities
Singularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
are allowed. More specifically a stratifold is stratified into differentiable manifolds of (possibly) different dimensions. Stratifolds can be used to construct new homology theories. For example, they provide a new geometric model for ordinary homology. The concept of stratifolds was invented by Matthias Kreck
Matthias Kreck
Matthias Kreck is a German mathematician who works in the areas of Algebraic Topology and Differential topology...
. The basic idea is similar to that of a topologically stratified space
Topologically stratified space
In topology, a branch of mathematics, a topologically stratified space is a space X that has been decomposed into pieces called strata; these strata are topological manifolds and are required to fit together in a certain way...
, but adapted to differential topology
Differential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
.
Definitions
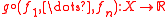Before we come to stratifolds, we define a preliminary notion, which captures the minimal notion for a smooth structure on a space: A differential space (in the sense of Sikorski) is a pair (X, C), where X is a topological space and C is a subalgebra of the continuous functions such that a function is in C if it is locally in C and is in C for smooth and . A simple example takes for X a smooth manifold and for C just the smooth functions.For a general differential space (X, C) and a point x in X we can define as in the case of manifolds a tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
as the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of all derivations
Derivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
of function germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
at x. Define strata
has dimension i. For an n-dimensional manifold M we have that and all other strata are empty. We are now ready for the definition of a stratifold, where more than one stratum may be non-empty:A k-dimensional stratifold is a differential space (S, C), where S is a locally compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
with countable base of topology. All skeleta should be closed. In addition we assume:
- The
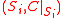are i-dimensional smooth manifolds. - For all x in S, restriction defines an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
stalksStalk (sheaf)The stalk of a sheaf is a mathematical construction capturing the behaviour of a sheaf around a given point.-Motivation and definition:Sheaves are defined on open sets, but the underlying topological space X consists of points. It is reasonable to attempt to isolate the behavior of a sheaf at a...
. - All tangent spaces have dimension ≤ k.
- For each x in S and every neighbourhood U of x, there exists a function
with 
and 
(a bump function).
A n-dimensional stratifold is called oriented if its (n − 1)-stratum is empty and its top stratum is oriented. One can also define stratifolds with boundary, the so-called c-stratifolds. One defines them as a pair
of topological spaces such that is an n-dimensional stratifold and is an (n − 1)-dimensional stratifold, together with an equivalence class of collars.An important subclass of stratifolds are the regular stratifolds, which can be roughly characterized as looking locally around a point in the i-stratum like the i-stratum times a (n − i)-dimensional stratifold. This is a condition which is fulfilled in most stratifold one usually encounters.
Examples
There are plenty of examples of stratifolds. The first example to consider is the open coneCone (topology)
In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
over a manifold M. We define a continuous function from S to the reals to be in C iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it is smooth on M × (0, 1) and it is locally constant around the cone point. The last condition is automatic by point 2 in the definition of a stratifold. We can substitute M by a stratifold S in this construction. The cone is oriented if and only if S is oriented and not zero-dimensional. If we consider the (closed) cone with bottom, we get a stratifold with boundary S.
Other examples for stratifolds are one-point compactifications and suspensions of manifolds, (real) algebraic varieties with only isolated singularities and (finite) simplicial complexes.
Bordism theories
In this section, we will assume all stratifolds to be regular. We call two maps from two oriented compact k-dimensional stratifolds into a space X bordantCobordism
In mathematics, cobordism is a fundamental equivalence relation on the class of compact manifolds of the same dimension, set up using the concept of the boundary of a manifold. Two manifolds are cobordant if their disjoint union is the boundary of a manifold one dimension higher. The name comes...
if there exists an oriented (k + 1)-dimensional compact stratifold T with boundary S + (−S
is denoted by . The sets have actually the structure of abelian groups with disjoint union as addition. One can develop enough differential topologyDifferential topology
In mathematics, differential topology is the field dealing with differentiable functions on differentiable manifolds. It is closely related to differential geometry and together they make up the geometric theory of differentiable manifolds.- Description :...
of stratifolds to show that these define a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
. Clearly,
for k > 0 since every oriented stratifold S is the boundary of its cone, which is oriented if dim(S) > 0. One can show that . Hence, by the Eilenberg–Steenrod uniqueness theorem, for every space X homotopy-equivalent to a CW-complex, where H denotes singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
. It should be noted, however, that for other spaces these two homology theories need not be isomorphic (an example is the one-point compactification of the surface of infinite genus).
There is also a simple way to define equivariant homology with the help of stratifolds. Let G be a compact Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
. We can then define a bordism theory of stratifolds mapping into a space X with a G-action just as above, only that we require all stratifolds to be equipped with an orientation-preserving free G-action and all maps to be G-equivariant. Denote by
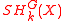the bordism classes. One can prove for every X homotopy equivalent to a CW-complex.Connection to the theory of genera
A genusGenus of a multiplicative sequence
In mathematics, the genus of a multiplicative sequence is a ring homomorphism, from the cobordism ring of smooth oriented compact manifolds to another ring, usually the ring of rational numbers.-Definition:...
is a ring homomorphism from a bordism ring into another ring. For example the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
defines a ring homomorphism
from the unoriented bordism ring and the signatureSignature (topology)
In the mathematical field of topology, the signature is an integer invariant which is defined for an oriented manifold M of dimension d=4k divisible by four ....
defines a ring homomorphism
from the oriented bordism ring. Here t has in the first case degree 1 and in the second case degree 4, since only manifolds in dimensions divisible by 4 can have non-zero signature. The left hand sides of these homomorphisms are homology theories evaluated at a point. With the help of stratifolds it is possible to construct homology theories such that the right hand sides are these homology theories evaluated at a point, the Euler homology and the Hirzebruch homology respectively.Umkehr maps
Suppose, one has a closed embedding of manifolds with oriented normal bundle. Then one can define an umkehr map . One possibility is to use stratifolds: represent a class 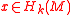by a stratifold 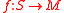. Then make ƒ transversal to N. The intersection of S and N defines a new stratifold S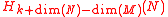. It is possible to repeat this construction in the context of an embedding of Hilbert manifoldHilbert manifold
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
s of finite codimension, which can be used in string topology
String topology
String topology, a branch of mathematics, is the study of algebraic structures on the homology of free loop spaces. The field was started by Chas and Sullivan in 1999 .-Motivation:...
.