String topology
Encyclopedia
String topology, a branch of mathematics
, is the study of algebraic structures on the homology
of free loop spaces. The field was started by Chas and Sullivan in 1999 (see Chas & Sullivan 1999).
of a space. Nevertheless, it is possible to construct such a structure for an oriented manifold
M of dimension d. This is the so-called intersection product. Intuitively, one can describe it as follows: given classes
and 
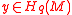, take their product 
and make it transversal to the diagonal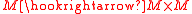 
. The intersection is then a class in 
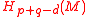, the intersection product of x and y. One way to make this construction rigorous is to use stratifold
s.
Another case, where the homology of a space has a product, is the (based) loop space
of a space X. Here the space itself has a product
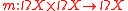
by going first the first loop and then the second. There is no analogous product structure for the free loop space LX of all maps from
to X since the two loops need not have a common point. A substitute for the map m is the map
where Map(8, M) is the subspace of
, where the value of the two loops coincides at 0 and 
is defined again by composing the loops. (Here "8" denotes the topological space "figure 8", i.e. the wedge of two circles.)
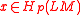and 
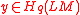. Their product 
lies in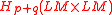 
. We need a map
One way to construct this is to use stratifolds (or another geometric definition of homology) to do transversal intersection (after interpreting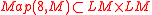
as an inclusion of Hilbert manifold
s). Another approach starts with the collapse map from LM x LM to the Thom space
of the normal bundle of Map(8, M). Composing the induced map in homology with the Thom isomorphism, we get the map we want.
Now we can compose i! with the induced map of
to get a class in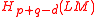 
, the Chas–Sullivan product of x and y (see eg Cohen & Jones 2002).
by rotation, which induces a map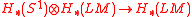
.
Plugging in the fundamental class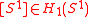
, gives an operator
of degree 1. One can show that this operator interacts nicely with the Chas–Sullivan product in the sense that they form together the structure of a Batalin-Vilkovisky algebra on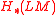
. This operator tends to be difficult to compute in general.
) an operation
which fulfills the usual axioms for a topological field theory. The Chas–Sullivan product is associated to the pair of pants. It can be shown that these operations are 0 if the genus of the surface is greater than 0 (see Tamanoi2010)
A more structured approach (exhibited in Godin2008) gives
the structure of a degree d open-closed homological conformal field theory (HCFT) with positive boundary. Ignoring the open-closed part, this amounts to the following structure: let S be a surface with boundary, where the boundary circles are labeled as incoming or outcoming. If there are p incoming and q outgoing and 
, we get operations
parametrized by a certain twisted homology of the mapping class group
of S.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, is the study of algebraic structures on the homology
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
of free loop spaces. The field was started by Chas and Sullivan in 1999 (see Chas & Sullivan 1999).
Motivation
While the singular cohomology of a space has always a product structure, this is not true for the singular homologySingular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
of a space. Nevertheless, it is possible to construct such a structure for an oriented manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M of dimension d. This is the so-called intersection product. Intuitively, one can describe it as follows: given classes
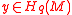and , take their product and make it transversal to the diagonal 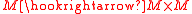. The intersection is then a class in 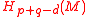, the intersection product of x and y. One way to make this construction rigorous is to use stratifoldStratifold
In differential topology, a branch of mathematics, a stratifold is a generalization of a differentiable manifold where certain kinds of singularities are allowed. More specifically a stratifold is stratified into differentiable manifolds of different dimensions. Stratifolds can be used to...
s.
Another case, where the homology of a space has a product, is the (based) loop space
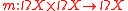
of a space X. Here the space itself has a productby going first the first loop and then the second. There is no analogous product structure for the free loop space LX of all maps from
to X since the two loops need not have a common point. A substitute for the map m is the mapwhere Map(8, M) is the subspace of
, where the value of the two loops coincides at 0 and is defined again by composing the loops. (Here "8" denotes the topological space "figure 8", i.e. the wedge of two circles.)The Chas–Sullivan product
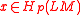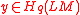The idea of the Chas–Sullivan product is to now combine in some way the product structures above. Consider two classes and . Their product lies in 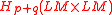. We need a mapOne way to construct this is to use stratifolds (or another geometric definition of homology) to do transversal intersection (after interpreting
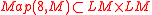as an inclusion of Hilbert manifoldHilbert manifold
In mathematics, a Hilbert manifold is a manifold modeled on Hilbert spaces. Thus it is a separable Hausdorff space in which each point has a neighbourhood homeomorphic to an infinite dimensional Hilbert space. The concept of a Hilbert manifold provides a possibility of extending the theory of...
s). Another approach starts with the collapse map from LM x LM to the Thom space
Thom space
In mathematics, the Thom space, Thom complex, or Pontryagin-Thom construction of algebraic topology and differential topology is a topological space associated to a vector bundle, over any paracompact space....
of the normal bundle of Map(8, M). Composing the induced map in homology with the Thom isomorphism, we get the map we want.
Now we can compose i! with the induced map of
to get a class in 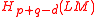, the Chas–Sullivan product of x and y (see eg Cohen & Jones 2002).Remarks
- As in the case of the intersection product, there are different sign conventions concerning the Chas–Sullivan product. In some convention, it is graded commutative, in some it is not.
- The same construction works if we replace
by another multiplicative homology theoryHomology theoryIn mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
h if M is oriented with respect to h.
- Furthermore, we can replace LM by
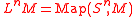. By an easy variation of the above construction, we get that 
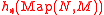is a module over 
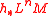if N is a manifold of dimensions n.
- The Serre spectral sequenceSerre spectral sequenceIn mathematics, the Serre spectral sequence is an important tool in algebraic topology...
is compatible with the above algebraic structures for both the fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
with fiber 
and the fiber bundle 
for a fiber bundle 
, which is important for computations (see Cohen&Jones&Yan2004 and Meier2010).
The Batalin-Vilkovisky structure
There is an action by rotation, which induces a map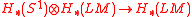.Plugging in the fundamental class
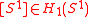, gives an operatorof degree 1. One can show that this operator interacts nicely with the Chas–Sullivan product in the sense that they form together the structure of a Batalin-Vilkovisky algebra on
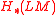. This operator tends to be difficult to compute in general.Field Theories
There are several attempts to construct (topological) field theories via string topology. The basic idea is to fix an oriented manifold M and associate to every surface with p incoming and q outgoing boundary components (with) an operationwhich fulfills the usual axioms for a topological field theory. The Chas–Sullivan product is associated to the pair of pants. It can be shown that these operations are 0 if the genus of the surface is greater than 0 (see Tamanoi2010)
A more structured approach (exhibited in Godin2008) gives
the structure of a degree d open-closed homological conformal field theory (HCFT) with positive boundary. Ignoring the open-closed part, this amounts to the following structure: let S be a surface with boundary, where the boundary circles are labeled as incoming or outcoming. If there are p incoming and q outgoing and , we get operationsparametrized by a certain twisted homology of the mapping class group
Mapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
of S.