Stencil codes
Encyclopedia
Stencil codes are a class of iterative kernels
which update array elements according to some fixed pattern, called stencil.
They are most commonly found in the codes
of computer simulations
, e.g. for computational fluid dynamics
in the context of scientific and engineering applications.
Other notable examples include solving partial differential equations, the Jacobi
kernel, the Gauss–Seidel method, image processing
and cellular automata
.
The regular structure of the arrays sets stencil codes apart from other modeling methods such as the Finite element method
. Most finite difference codes
which operate on regular grids can be formulated as stencil codes.
) those need to be adjusted during the course of the computation as well. Since the stencil is the same for each element, the pattern of data accesses is repeated.
More formally, we may define stencil codes as a 5-tuple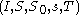
with the following meaning:
Since I is a k-dimensional integer interval, the array will always have the topology of a finite regular grid. The array is also called simulation space and individual cells are identified by their index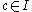
. The stencil is an ordered set of 
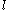relative coordinates. We can now obtain for each cell 
the tuple of its neighbors indices 
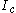
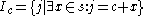
Their states are given by mapping the tuple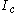
to the corresponding tuple of states 
:
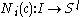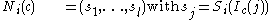
This is all we need to define the system's state for the following time steps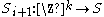
with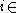 
:
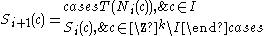
Note that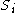
is defined on 
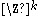and not just on 
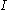since the boundary conditions need to be set, too. Sometimes the elements of 
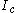may be defined by a vector addition modulo the simulation space's dimension to realize toroidal topologies:
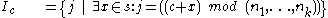
This may be useful for implementing Periodic boundary conditions
, which simplifies certain physical models.
iteration can be defined. The update function computes the arithmetic mean of a cell's four neighbors. In this case we set off with an initial solution of 0. The left and right boundary are fixed at 1, while the upper and lower boundaries are set to 0. After a sufficient number of iterations, the system converges against a saddle-shape.
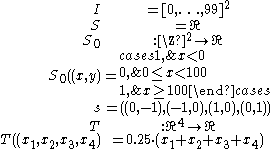
and Moore neighborhood
. The example above uses a 2D von Neumann stencil while LBM codes generally use its 3D variant. Conway's Game of Life
uses the 2D Moore neighborhood. That said, other stencils such as a 25-point stencil for seismic wave propagation can be found, too.
This is challenging since the computations are tightly coupled (because of the cell updates depending on neighboring cells) and most stencil codes are memory bound (i.e. the ratio of memory accesses and calculations is high).
Virtually all current parallel architectures have been explored for executing stencil codes efficiently;
at the moment GPGPUs
have proven to be most efficient.
and their high computational requirements, there are a number of efforts which aim at creating reusable libraries to support scientists in implementing new stencil codes. The libraries are mostly concerned with the parallelization, but may also tackle other challenges, such as IO, steering
and checkpointing
. They may be classified by their API.
. The disadvantage is that the library can not handle cache blocking (as this has to be done within the loops)
or wrapping of the code for accelerators (e.g. via CUDA or OpenCL). Notable implementations include Cactus, a physics problem solving environment, and waLBerla.
but also to run the same code on multi-cores and GPUs. This approach requires the user to recompile his source code together with the library. Otherwise a function call for every cell update would be required, which would seriously impair performance. This is only feasible with techniques such as class templates
or metaprogramming
, which is also the reason why this design is only found in newer libraries. Examples are Physis and LibGeoDecomp.
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
which update array elements according to some fixed pattern, called stencil.
They are most commonly found in the codes
Source code
In computer science, source code is text written using the format and syntax of the programming language that it is being written in. Such a language is specially designed to facilitate the work of computer programmers, who specify the actions to be performed by a computer mostly by writing source...
of computer simulations
Computer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
, e.g. for computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
in the context of scientific and engineering applications.
Other notable examples include solving partial differential equations, the Jacobi
Jacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
kernel, the Gauss–Seidel method, image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and cellular automata
Cellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
.
The regular structure of the arrays sets stencil codes apart from other modeling methods such as the Finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
. Most finite difference codes
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
which operate on regular grids can be formulated as stencil codes.
Definition
Stencil codes perform a sequence of sweeps (called timesteps) through a given array. Generally this is a 2- or 3-dimensional regular grid. The elements of the arrays are often referred to as cells. In each timestep, the stencil code updates all array elements. Using neighboring array elements in a fixed pattern (called the stencil), each cell's new value is computed. In most cases boundary values are left unchanged, but in some cases (e.g. LBM codesLattice Boltzmann methods
Lattice Boltzmann methods is a class of computational fluid dynamics methods for fluid simulation. Instead of solving the Navier–Stokes equations, the discrete Boltzmann equation is solved to simulate the flow of a Newtonian fluid with collision models such as Bhatnagar-Gross-Krook...
) those need to be adjusted during the course of the computation as well. Since the stencil is the same for each element, the pattern of data accesses is repeated.
More formally, we may define stencil codes as a 5-tuple
with the following meaning:-
is the index set. It defines the topology of the array. -
is the (not necessarily finite) set of states, one of which each cell may take on on any given timestep. -
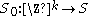defines the initial state of the system at time 0. -
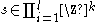is the stencil itself and describes the actual shape of the neighborhood. (There are 
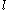elements in the stencil. -
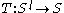is the transition function which is used to determine a cell's new state, depending on its neighbors.
Since I is a k-dimensional integer interval, the array will always have the topology of a finite regular grid. The array is also called simulation space and individual cells are identified by their index
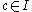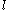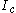
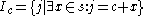
. The stencil is an ordered set of relative coordinates. We can now obtain for each cell the tuple of its neighbors indices Their states are given by mapping the tuple
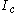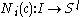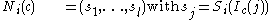
to the corresponding tuple of states :This is all we need to define the system's state for the following time steps
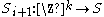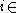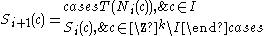
with :Note that
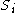is defined on 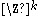and not just on 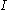since the boundary conditions need to be set, too. Sometimes the elements of 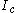may be defined by a vector addition modulo the simulation space's dimension to realize toroidal topologies: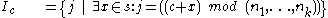This may be useful for implementing Periodic boundary conditions
Periodic boundary conditions
In mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
, which simplifies certain physical models.
Example: 2D Jacobi Iteration
To illustrate the formal definition, we'll have a look at how a two dimensional JacobiJacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
iteration can be defined. The update function computes the arithmetic mean of a cell's four neighbors. In this case we set off with an initial solution of 0. The left and right boundary are fixed at 1, while the upper and lower boundaries are set to 0. After a sufficient number of iterations, the system converges against a saddle-shape.
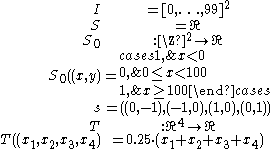
Stencils
The shape of the neighborhood used during the updates depends on the application itself. The most common stencils are the 2D or 3D versions of the Von Neumann neighborhoodVon Neumann neighborhood
In cellular automata, the von Neumann neighborhood comprises the four cells orthogonally surrounding a central cell on a two-dimensional square lattice. The neighborhood is named after John von Neumann, who used it for his pioneering cellular automata including the Universal Constructor...
and Moore neighborhood
Moore neighborhood
In cellular automata, the Moore neighborhood comprises the eight cells surrounding a central cell on a two-dimensional square lattice. The neighborhood is named after Edward F. Moore, a pioneer of cellular automata theory. It is one of the two most commonly used neighborhood types, the other one...
. The example above uses a 2D von Neumann stencil while LBM codes generally use its 3D variant. Conway's Game of Life
Conway's Game of Life
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
uses the 2D Moore neighborhood. That said, other stencils such as a 25-point stencil for seismic wave propagation can be found, too.
Implementation Issues
Many simulation codes may be formulated naturally as stencil codes. Since computing time and memory consumption grow linearly wth the number of array elements, parallel implementations of stencil codes are of paramount importance to research.This is challenging since the computations are tightly coupled (because of the cell updates depending on neighboring cells) and most stencil codes are memory bound (i.e. the ratio of memory accesses and calculations is high).
Virtually all current parallel architectures have been explored for executing stencil codes efficiently;
at the moment GPGPUs
GPGPU
General-purpose computing on graphics processing units is the technique of using a GPU, which typically handles computation only for computer graphics, to perform computation in applications traditionally handled by the CPU...
have proven to be most efficient.
Libraries
Due to both, the importance of stencil codes to computer simulationsComputer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
and their high computational requirements, there are a number of efforts which aim at creating reusable libraries to support scientists in implementing new stencil codes. The libraries are mostly concerned with the parallelization, but may also tackle other challenges, such as IO, steering
Computational steering
Computational steering is the practice of manually intervening with an otherwise autonomous computational process, to change its outcome. The term is commonly used within the numerical simulation community, where it more specifically refers to the practice of interactively guiding a computational...
and checkpointing
Application checkpointing
Checkpointing is a technique for inserting fault tolerance into computing systems. It basically consists of storing a snapshot of the current application state, and later on, use it for restarting the execution in case of failure.- Technique properties :...
. They may be classified by their API.
Patch-Based Libraries
This is a traditional design. The library manages a set of n-dimensional scalar arrays, which the user code may access to perform updates. The library handles the synchronization of the boundaries (dubbed ghost zone or halo). The advantage of this interface is that the user code may loop over the arrays, which makes it easy to integrate legacy codes. The disadvantage is that the library can not handle cache blocking (as this has to be done within the loops)
or wrapping of the code for accelerators (e.g. via CUDA or OpenCL). Notable implementations include Cactus, a physics problem solving environment, and waLBerla.
Cell-Based Libraries
These libraries move the interface to updating single simulation cells: only the current cell and its neighbors are exposed to the user code, e.g. via getter/setter methods. The advantage of this approach is that the library can control tightly which cells are updated in which order, which is useful not only to implement cache blocking,but also to run the same code on multi-cores and GPUs. This approach requires the user to recompile his source code together with the library. Otherwise a function call for every cell update would be required, which would seriously impair performance. This is only feasible with techniques such as class templates
Template (programming)
Templates are a feature of the C++ programming language that allow functions and classes to operate with generic types. This allows a function or class to work on many different data types without being rewritten for each one....
or metaprogramming
Metaprogramming
Metaprogramming is the writing of computer programs that write or manipulate other programs as their data, or that do part of the work at compile time that would otherwise be done at runtime...
, which is also the reason why this design is only found in newer libraries. Examples are Physis and LibGeoDecomp.
See also
- Finite difference methodFinite difference methodIn mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
- Computer simulationComputer simulationA computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
- Five-point stencilFive-point stencilIn numerical analysis, given a square grid in one or two dimensions, the five-point stencil of a point in the grid is made up of the point itself together with its four "neighbors"...
- Stencil jumpingStencil jumpingStencil jumping, at times called stencil walking, is an algorithm to locate the grid element enclosing a given point for any structured mesh...