
Statistical proof
Encyclopedia
.
Statistical proof is the rational demonstration of degree of certainty for a proposition, hypothesis or theory to convince others subsequent to a statistical test of the increased understanding of the facts. Statistical methods are used to demonstrate the validity and logic of inference
with explicit reference to a hypotheses, the experimental
data
, the facts
, the test, and the odds
. Proof
has two essential aims, the first is to convince and the second is to explain the proposition through peer and public review.
The burden of proof
rests on the demonstrable application of the statistical method, disclosure of the assumptions, and the relevance that the test has with respect to a genuine understanding of the data relative to the external world. There are adherents to several different statistical philosophies of inference, such as Bayes theorem versus the likelihood function
, or positivism
versus critical rationalism
. These methods of reason have direct bearing on statistical proof and its interpretations in the broader philosophy of science.
A common demarcation between science and non-science is the hypothetico-deductive proof of falsification developed by Karl Popper
, which is consistent within the traditions of statistics. Other modes of inference, however, may include the inductive and abductive modes of proof. Scientists do not use statistical proof as a means to attain certainty, but to falsify
claims and explain theory
. Science cannot achieve absolute certainty nor is it a continuous march toward an objective truth as the vernacular as opposed to the scientific meaning of the term "proof" might imply. Statistical proof offers a kind of proof of a theories falsity and the means to learn heuristically through repeated statistical trials and experimental error. Statistical proof also has applications in legal matters with implications for the legal burden of proof.
The preceding axioms provide the statistical proof and basis for the laws
of randomness, or objective chance from where modern statistical theory has since progressed. Experimental data, however, can never prove that the hypotheses (h) is true, but relies on an inductive inference by measuring the probability of the hypotheses relative to the empirical data. The proof is in the rational demonstration of using the logic of inference
, math
, testing
, and deductive reasoning
of significance
.
that give exact descriptions of variables that behave according to natural laws
of random chance
. When a statistical test is applied to samples of a population, the test determines if the sample statistics are significantly different from the assumed null-model. True values of a population, which are unknowable in practice, are called parameters of the population. Researchers sample from populations, which provide estimates of the parameters, to calculate the mean or standard deviation. If the entire population is sampled, then the sample statistic mean and distribution will converge with the parametric distribution.
Using the scientific method of falsification, the probability value
that the sample statistic is sufficiently different from the null-model than can be explained by chance alone is given prior to the test. Most statisticians set the prior probability value at 0.05 or 0.1, which means if the sample statistics diverge from the parametric model more than 5 (or 10) times out of 100, then the discrepancy is unlikely to be explained by chance alone and the null-hypothesis is rejected. Statistical models provide exact outcomes of the parametric and estimates of the sample statistics. Hence, the burden of proof
rests in the sample statistics that provide estimates of a statistical model. Statistical models contain the mathematical proof
of the parametric values and their probability distributions.
Bayesian statistics
are based on a different philosophical approach for proof of inference
. The mathematical formula for Bayes's theorem is:

The formula is read as the probability of the parameter (or hypothesis =h, as used in the notation on axioms) “given” the data (or empirical observation), where the horizontal bar refers to "given". The right hand side of the formula calculates the prior probability of a statistical model (Pr [Parameter]) with the likelihood
(Pr [Data | Parameter]) to produce a posterior probability distribution of the parameter (Pr [Parameter | Data]). The posterior probability is the likelihood that the parameter is correct given the observed data or samples statistics. Hypotheses can be compared using Bayesian inference by means of the Bayes factor, which is the ratio of the posterior odds to the prior odds. It provides a measure of the data and if it has increased or decreased the likelihood of one hypotheses relative to another.
The statistical proof is the Bayesian demonstration that one hypothesis has a higher (weak, strong, positive) likelihood. There is considerable debate if the Bayesian method aligns with Karl Poppers method of proof of falsification, where some have suggested that "...there is no such thing as "accepting" hypotheses at all. All that one does in science is assign degrees of belief..." According to Popper, hypotheses that have withstood testing and have yet to be falsified are not verified but corroborated
. Some researches have suggested that Popper's quest to define corroboration on the premise of probability put his philosophy in line with the Bayesian approach. In this context, the likelihood of one hypothesis relative to another may be an index of corroboration, not confirmation, and thus statistically proven through rigorous objective standing.
Statistical proof was not regularly applied in decisions concerning United States legal proceedings until the mid 1970's following a landmark jury discrimination case in Castaneda v. Partida. The US Supreme Court ruled that gross statistical disparities constitutes "prima facie
proof" of discrimination, resulting in a shift of the burden of proof from plaintiff to defendant. Since that ruling, statistical proof has been used in many other cases on inequality, discrimination, and DNA evidence. However, there is not a one-to-one correspondence between statistical proof and the legal burden of proof. "The Supreme Court has stated that the degrees of rigor required in the factfinding processes of law and science do not necessarily correspond."
In an example of a death row sentence (McCleskey v. Kemp) concerning racial discrimination, the petitioner, a black man named McCleskey was charged with the murder of a white police officer during a robbery. Expert testimony for McClesky introduced a statistical proof showing that "defendants charged with killing white victims were 4.3 times as likely to receive a death sentence as charged with killing blacks.". Nonetheless, the statistics was insufficient "to prove that the decisionmakers in his case acted with discriminatory purpose." It was further argued that there were "inherent limitations of the statistical proof", because it did not refer to the specifics of the individual. Despite the statistical demonstration of an increased probability of discrimination, the legal burden of proof (it was argued) had to be examined on a case by case basis.
Statistical proof is the rational demonstration of degree of certainty for a proposition, hypothesis or theory to convince others subsequent to a statistical test of the increased understanding of the facts. Statistical methods are used to demonstrate the validity and logic of inference
Inference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
with explicit reference to a hypotheses, the experimental
Experiment
An experiment is a methodical procedure carried out with the goal of verifying, falsifying, or establishing the validity of a hypothesis. Experiments vary greatly in their goal and scale, but always rely on repeatable procedure and logical analysis of the results...
data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
, the facts
Facts
Facts usually refers to the usage as a plural noun of fact, an incontrovertible truth.Facts may also refer to:*Carroll, Lewis, who wrote a poem called "Facts"*FACTS , program produced by Asia Television in Hong Kong....
, the test, and the odds
Odds
The odds in favor of an event or a proposition are expressed as the ratio of a pair of integers, which is the ratio of the probability that an event will happen to the probability that it will not happen...
. Proof
Proof
Proof may refer to:* Proof , sufficient evidence or argument for the truth of a proposition* Formal proof* Mathematical proof, a convincing demonstration that some mathematical statement is necessarily true...
has two essential aims, the first is to convince and the second is to explain the proposition through peer and public review.
The burden of proof
Philosophic burden of proof
The philosophic burden of proof is the obligation on a party in an epistemic dispute to provide sufficient warrant for their position.-Holder of the burden:When debating any issue, there is an implicit burden of proof on the person asserting a claim...
rests on the demonstrable application of the statistical method, disclosure of the assumptions, and the relevance that the test has with respect to a genuine understanding of the data relative to the external world. There are adherents to several different statistical philosophies of inference, such as Bayes theorem versus the likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
, or positivism
Positivism
Positivism is a a view of scientific methods and a philosophical approach, theory, or system based on the view that, in the social as well as natural sciences, sensory experiences and their logical and mathematical treatment are together the exclusive source of all worthwhile information....
versus critical rationalism
Critical rationalism
Critical rationalism is an epistemological philosophy advanced by Karl Popper. Popper wrote about critical rationalism in his works, The Open Society and its Enemies Volume 2, and Conjectures and Refutations.- Criticism, not support :...
. These methods of reason have direct bearing on statistical proof and its interpretations in the broader philosophy of science.
A common demarcation between science and non-science is the hypothetico-deductive proof of falsification developed by Karl Popper
Karl Popper
Sir Karl Raimund Popper, CH FRS FBA was an Austro-British philosopher and a professor at the London School of Economics...
, which is consistent within the traditions of statistics. Other modes of inference, however, may include the inductive and abductive modes of proof. Scientists do not use statistical proof as a means to attain certainty, but to falsify
Falsifiability
Falsifiability or refutability of an assertion, hypothesis or theory is the logical possibility that it can be contradicted by an observation or the outcome of a physical experiment...
claims and explain theory
Scientific theory
A scientific theory comprises a collection of concepts, including abstractions of observable phenomena expressed as quantifiable properties, together with rules that express relationships between observations of such concepts...
. Science cannot achieve absolute certainty nor is it a continuous march toward an objective truth as the vernacular as opposed to the scientific meaning of the term "proof" might imply. Statistical proof offers a kind of proof of a theories falsity and the means to learn heuristically through repeated statistical trials and experimental error. Statistical proof also has applications in legal matters with implications for the legal burden of proof.
Axioms
There are two kinds of axioms, 1) conventions that are taken as true that should be avoided because they cannot be tested, and 2) hypotheses. Proof in the theory of probability was built on four axioms developed in the late 17th century:- The probability of a hypotheses is a non-negative real number:
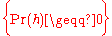 ;
; - The probability of necessary truth equals one:
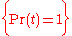 ;
; - If two hypotheses h1 and h2 are mutually exclusive, then the sum of their probabilities is equal to the probability of their disjunctionLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
: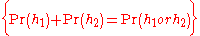 ;
; - The conditional probability of h1 given h2
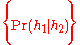 is equal to the unconditional probability
is equal to the unconditional probability 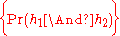 of the conjunction h1 and h2, divided by the unconditional probability
of the conjunction h1 and h2, divided by the unconditional probability  of h2 where that probability is positive
of h2 where that probability is positive 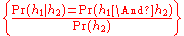 , where
, where  .
.
The preceding axioms provide the statistical proof and basis for the laws
Scientific law
A scientific law is a statement that explains what something does in science just like Newton's law of universal gravitation. A scientific law must always apply under the same conditions, and implies a causal relationship between its elements. The law must be confirmed and broadly agreed upon...
of randomness, or objective chance from where modern statistical theory has since progressed. Experimental data, however, can never prove that the hypotheses (h) is true, but relies on an inductive inference by measuring the probability of the hypotheses relative to the empirical data. The proof is in the rational demonstration of using the logic of inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
, math
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
, testing
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
, and deductive reasoning
Reason
Reason is a term that refers to the capacity human beings have to make sense of things, to establish and verify facts, and to change or justify practices, institutions, and beliefs. It is closely associated with such characteristically human activities as philosophy, science, language, ...
of significance
Statistical significance
In statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
.
Test and proof
Statistical tests are formulated on models that generate probability distributions. Examples of probability distributions might include the binary, normal, or poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
that give exact descriptions of variables that behave according to natural laws
Natural law
Natural law, or the law of nature , is any system of law which is purportedly determined by nature, and thus universal. Classically, natural law refers to the use of reason to analyze human nature and deduce binding rules of moral behavior. Natural law is contrasted with the positive law Natural...
of random chance
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
. When a statistical test is applied to samples of a population, the test determines if the sample statistics are significantly different from the assumed null-model. True values of a population, which are unknowable in practice, are called parameters of the population. Researchers sample from populations, which provide estimates of the parameters, to calculate the mean or standard deviation. If the entire population is sampled, then the sample statistic mean and distribution will converge with the parametric distribution.
Using the scientific method of falsification, the probability value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
that the sample statistic is sufficiently different from the null-model than can be explained by chance alone is given prior to the test. Most statisticians set the prior probability value at 0.05 or 0.1, which means if the sample statistics diverge from the parametric model more than 5 (or 10) times out of 100, then the discrepancy is unlikely to be explained by chance alone and the null-hypothesis is rejected. Statistical models provide exact outcomes of the parametric and estimates of the sample statistics. Hence, the burden of proof
Philosophic burden of proof
The philosophic burden of proof is the obligation on a party in an epistemic dispute to provide sufficient warrant for their position.-Holder of the burden:When debating any issue, there is an implicit burden of proof on the person asserting a claim...
rests in the sample statistics that provide estimates of a statistical model. Statistical models contain the mathematical proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
of the parametric values and their probability distributions.
Bayes theorem
Bayesian statistics
Bayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
are based on a different philosophical approach for proof of inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
. The mathematical formula for Bayes's theorem is:

The formula is read as the probability of the parameter (or hypothesis =h, as used in the notation on axioms) “given” the data (or empirical observation), where the horizontal bar refers to "given". The right hand side of the formula calculates the prior probability of a statistical model (Pr [Parameter]) with the likelihood
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
(Pr [Data | Parameter]) to produce a posterior probability distribution of the parameter (Pr [Parameter | Data]). The posterior probability is the likelihood that the parameter is correct given the observed data or samples statistics. Hypotheses can be compared using Bayesian inference by means of the Bayes factor, which is the ratio of the posterior odds to the prior odds. It provides a measure of the data and if it has increased or decreased the likelihood of one hypotheses relative to another.
The statistical proof is the Bayesian demonstration that one hypothesis has a higher (weak, strong, positive) likelihood. There is considerable debate if the Bayesian method aligns with Karl Poppers method of proof of falsification, where some have suggested that "...there is no such thing as "accepting" hypotheses at all. All that one does in science is assign degrees of belief..." According to Popper, hypotheses that have withstood testing and have yet to be falsified are not verified but corroborated
Corroborating evidence
Corroborating evidence is evidence that tends to support a proposition that is already supported by some evidence, therefore confirming the proposition. For example, W, a witness, testifies that she saw X drive his automobile into a green car...
. Some researches have suggested that Popper's quest to define corroboration on the premise of probability put his philosophy in line with the Bayesian approach. In this context, the likelihood of one hypothesis relative to another may be an index of corroboration, not confirmation, and thus statistically proven through rigorous objective standing.
In legal proceedings
Statistical proof in a legal proceeding can be sorted into three categories of evidence:- The occurrence of an event, act, or type of conduct,
- The identity the individual(s) responsible
- The intent or psychological responsibility
Statistical proof was not regularly applied in decisions concerning United States legal proceedings until the mid 1970's following a landmark jury discrimination case in Castaneda v. Partida. The US Supreme Court ruled that gross statistical disparities constitutes "prima facie
Prima facie
Prima facie is a Latin expression meaning on its first encounter, first blush, or at first sight. The literal translation would be "at first face", from the feminine form of primus and facies , both in the ablative case. It is used in modern legal English to signify that on first examination, a...
proof" of discrimination, resulting in a shift of the burden of proof from plaintiff to defendant. Since that ruling, statistical proof has been used in many other cases on inequality, discrimination, and DNA evidence. However, there is not a one-to-one correspondence between statistical proof and the legal burden of proof. "The Supreme Court has stated that the degrees of rigor required in the factfinding processes of law and science do not necessarily correspond."
In an example of a death row sentence (McCleskey v. Kemp) concerning racial discrimination, the petitioner, a black man named McCleskey was charged with the murder of a white police officer during a robbery. Expert testimony for McClesky introduced a statistical proof showing that "defendants charged with killing white victims were 4.3 times as likely to receive a death sentence as charged with killing blacks.". Nonetheless, the statistics was insufficient "to prove that the decisionmakers in his case acted with discriminatory purpose." It was further argued that there were "inherent limitations of the statistical proof", because it did not refer to the specifics of the individual. Despite the statistical demonstration of an increased probability of discrimination, the legal burden of proof (it was argued) had to be examined on a case by case basis.

