In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a set  in the Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 Rⁿ is called a star domain (or star-convex set, star-shaped or radially convex set) if there exists in such that for all in the line segment

Line segment

In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...

 from to is in This definition is immediately generalizable to any real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 or complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

 vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

.

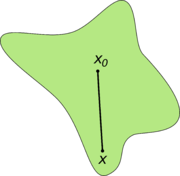
Intuitively, if one thinks of S as of a region surrounded by a wall, S is a star domain if one can find a vantage point x₀ in S from which any point x in S is within line-of-sight.

Examples

• Any line or plane in Rⁿ is a star domain.
• A line or a plane without a point is not a star domain.
• If A is a set in Rⁿ, the set

obtained by connecting any point in A to the origin is a star domain.

Properties

• Any non-empty convex set
  Convex set
  In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
  
   is a star domain. A set is convex if and only if it is a star domain with respect to any point in that set.
• A cross
  Cross
  A cross is a geometrical figure consisting of two lines or bars perpendicular to each other, dividing one or two of the lines in half. The lines usually run vertically and horizontally; if they run obliquely, the design is technically termed a saltire, although the arms of a saltire need not meet...
  
  -shaped figure is a star domain but is not convex.
• The closure
  Closure (topology)
  In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
  
   of a star domain is a star domain, but the interior
  Interior (topology)
  In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
  
   of a star domain is not necessarily a star domain.
• Any star domain is a contractible
  Contractible space
  In mathematics, a topological space X is contractible if the identity map on X is null-homotopic, i.e. if it is homotopic to some constant map. Intuitively, a contractible space is one that can be continuously shrunk to a point....
  
   set, via a straight-line homotopy
  Homotopy
  In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
  
  . In particular, any star domain is a simply connected set.
• The union and intersection of two star domains is not necessarily a star domain.
• A nonempty open star domain S in Rⁿ is diffeomorphic
  Diffeomorphism
  In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
  
   to Rⁿ.

See also

• Art gallery problem
  Art gallery problem
  The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from a real-world problem of guarding an art gallery with the minimum number of guards which together can observe the whole gallery...
  
  
• Star polygon — an unrelated term
• Star-shaped polygon
  Star-shaped polygon
  A star-shaped polygon is a polygonal region in the plane which is a star domain, i.e., a polygon P is star-shaped, if there exists a point z such that for each point p of P the segment zp lies entirely within P.The set of all points z with the described property is called the kernel of...
  
  
• Balanced set
  Balanced set
  In linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space is a set S so that for all scalars α with |α| ≤ 1\alpha S \subseteq S...