
Art gallery problem
Encyclopedia
The art gallery problem or museum problem is a well-studied visibility problem in computational geometry
. It originates from a real-world problem of guarding an art gallery
with the minimum number of guards which together can observe the whole gallery. In the computational geometry version of the problem the layout of the art gallery is represented by a simple polygon
and each guard is represented by a point
in the polygon. A set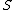 of points is said to guard a polygon if, for every point
of points is said to guard a polygon if, for every point 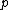 in the polygon, there is some
in the polygon, there is some 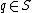 such that the line segment
such that the line segment
between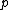 and
and 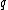 does not leave the polygon.
does not leave the polygon.
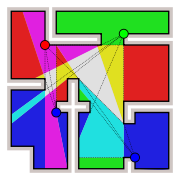 There are numerous variations of the original problem that are also referred to as the art gallery problem. In some versions guards are restricted to the perimeter, or even to the vertices of the polygon. Some versions require only the perimeter or a subset of the perimeter to be guarded.
There are numerous variations of the original problem that are also referred to as the art gallery problem. In some versions guards are restricted to the perimeter, or even to the vertices of the polygon. Some versions require only the perimeter or a subset of the perimeter to be guarded.
Solving the version in which guards must be placed on vertices and only vertices need to be guarded is equivalent to solving the dominating set problem on the visibility graph
of the polygon.
, gives an upper bound
on the minimal number of guards. It states that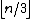 guards are always sufficient and sometimes necessary to guard a simple polygon with
guards are always sufficient and sometimes necessary to guard a simple polygon with  vertices.
vertices.
The question about how many vertices/watchmen/guards were needed was posed to Chvátal by Victor Klee
in 1973. Chvátal proved it shortly thereafter. Chvátal's proof was later simplified by Steve Fisk, via a 3-coloring
argument.
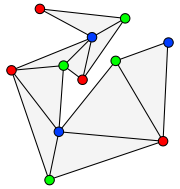 proves the art gallery theorem as follows.
proves the art gallery theorem as follows.
First, the polygon is triangulated
(without adding extra vertices). The vertices of the polygon are then 3-colored
in such a way that every triangle has all three colors. To find a 3-coloring, it is helpful to observe that the dual graph
to the triangulation (the undirected graph having one vertex per triangle and one edge per pair of adjacent triangles) is a tree
, for any cycle in the dual graph would form the boundary of a hole in the polygon, contrary to the assumption that it has no holes. Whenever there is more than one triangle, the dual graph (like any tree) must have a vertex with only one neighbor, corresponding to a triangle that is adjacent to other triangles along only one of its sides. The simpler polygon formed by removing this triangle has a 3-coloring by mathematical induction
, and this coloring is easily extended to the one additional vertex of the removed triangle.
Once a 3-coloring is found, the vertices with any one color form a valid guard set, because every triangle of the polygon is guarded by its vertex with that color. Since the three colors partition the n vertices of the polygon, the color with the fewest vertices forms a valid guard set with at most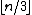 guards.
guards.
There are a number of other generalizations and specializations of the original art-gallery theorem. For instance, for orthogonal polygons, those whose edges/walls meet at right angles, only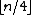 guards are needed. There are at least three distinct proofs of this result, none of them simple: by Kahn, Klawe
guards are needed. There are at least three distinct proofs of this result, none of them simple: by Kahn, Klawe
, and Kleitman
; by Lubiw; and by Sack
and Toussaint
.
A related problem asks for the number of guards to cover the exterior of an arbitrary polygon (the "Fortress Problem"):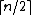 are sometimes necessary and always sufficient. In other words, the infinite exterior is more challenging to cover than the finite interior.
are sometimes necessary and always sufficient. In other words, the infinite exterior is more challenging to cover than the finite interior.
versions of the art gallery problem, one is given as input both a polygon and a number k, and must determine whether the polygon can be guarded with k or fewer guards. This problem and all of its standard variations (such as restricting the guard locations to vertices or edges of the polygon) are NP-hard
.
Regarding approximation algorithm
s for the minimum number of guards, proved the problem to be APX-hard, implying that it is unlikely that any approximation ratio better than some fixed constant can be achieved by a polynomial time approximation algorithm
. However, a constant approximation ratio is not known. Instead, a logarithm
ic approximation may be achieved for the minimum number of vertex guards by reducing the problem to a set cover problem. As showed, the set system derived from an art gallery problem has bounded VC dimension
, allowing the application of set cover algorithms based on ε-nets
whose approximation ratio is the logarithm of the optimal number of guards rather than of the number of polygon vertices.
For unrestricted guards, the infinite number of potential guard positions makes the problem even more difficult.
However, efficient algorithms are known for finding a set of at most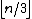 vertex guards, matching Chvátal's upper bound.
vertex guards, matching Chvátal's upper bound.
proved that a placement for these guards may be computed in O(n log n) time in the worst case, via a divide and conquer algorithm
.
gave a linear time algorithm by using Fisk's short proof and Bernard Chazelle
's linear time plane triangulation algorithm.
An exact algorithm was proposed by for vertex guards. The authors conducted extensive computational experiments with several classes of polygons showing that optimal solutions can be found in relatively small computation times even for instances associated to thousands of vertices. The input data and the optimal solutions for these instances are available for download.
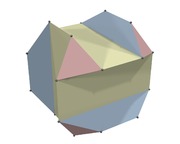 If a museum is represented in three dimensions as a polyhedron
If a museum is represented in three dimensions as a polyhedron
, then putting a guard at each vertex will not ensure that all of the museum is under observation. Although all of the surface of the polyhedron would be surveyed, for some polyhedra there are points in the interior which might not be under surveillance.
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
. It originates from a real-world problem of guarding an art gallery
Art gallery
An art gallery or art museum is a building or space for the exhibition of art, usually visual art.Museums can be public or private, but what distinguishes a museum is the ownership of a collection...
with the minimum number of guards which together can observe the whole gallery. In the computational geometry version of the problem the layout of the art gallery is represented by a simple polygon
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
and each guard is represented by a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in the polygon. A set
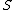 of points is said to guard a polygon if, for every point
of points is said to guard a polygon if, for every point 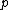 in the polygon, there is some
in the polygon, there is some 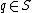 such that the line segment
such that the line segmentLine segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
between
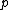 and
and 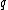 does not leave the polygon.
does not leave the polygon.Two dimensions

Solving the version in which guards must be placed on vertices and only vertices need to be guarded is equivalent to solving the dominating set problem on the visibility graph
Visibility graph
In computational geometry and robot motion planning, a visibility graph is a graph of intervisible locations, typically for a set of points and obstacles in the Euclidean plane. Each node in the graph represents a point location, and each edge represents a visible connection between them...
of the polygon.
Chvátal's art gallery theorem
Chvátal's art gallery theorem, named after Václav ChvátalVáclav Chvátal
Václav Chvátal is a professor in the Department of Computer Science and Software Engineering at Concordia University in Montreal, Canada, where he holds theCanada Research Chair in Combinatorial Optimization....
, gives an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the minimal number of guards. It states that
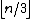 guards are always sufficient and sometimes necessary to guard a simple polygon with
guards are always sufficient and sometimes necessary to guard a simple polygon with  vertices.
vertices.The question about how many vertices/watchmen/guards were needed was posed to Chvátal by Victor Klee
Victor Klee
Victor L. Klee, Jr. was a mathematician specialising in convex sets, functional analysis, analysis of algorithms, optimization, and combinatorics. He spent almost his entire career at the University of Washington in Seattle.Born in San Francisco, Vic Klee earned his B.A...
in 1973. Chvátal proved it shortly thereafter. Chvátal's proof was later simplified by Steve Fisk, via a 3-coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
argument.
Fisk's short proof

First, the polygon is triangulated
Polygon triangulation
In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding the set of triangles with pairwise non-intersecting interiors whose union is P....
(without adding extra vertices). The vertices of the polygon are then 3-colored
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
in such a way that every triangle has all three colors. To find a 3-coloring, it is helpful to observe that the dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
to the triangulation (the undirected graph having one vertex per triangle and one edge per pair of adjacent triangles) is a tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
, for any cycle in the dual graph would form the boundary of a hole in the polygon, contrary to the assumption that it has no holes. Whenever there is more than one triangle, the dual graph (like any tree) must have a vertex with only one neighbor, corresponding to a triangle that is adjacent to other triangles along only one of its sides. The simpler polygon formed by removing this triangle has a 3-coloring by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
, and this coloring is easily extended to the one additional vertex of the removed triangle.
Once a 3-coloring is found, the vertices with any one color form a valid guard set, because every triangle of the polygon is guarded by its vertex with that color. Since the three colors partition the n vertices of the polygon, the color with the fewest vertices forms a valid guard set with at most
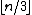 guards.
guards.Generalizations
Chvátal's upper bound remains valid if the restriction to guards at corners is loosened to guards at any point not exterior to the polygon.There are a number of other generalizations and specializations of the original art-gallery theorem. For instance, for orthogonal polygons, those whose edges/walls meet at right angles, only
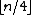 guards are needed. There are at least three distinct proofs of this result, none of them simple: by Kahn, Klawe
guards are needed. There are at least three distinct proofs of this result, none of them simple: by Kahn, KlaweMaria Klawe
Maria M. Klawe is a computer scientist and the fifth president of Harvey Mudd College . Although born in Toronto in 1951, she became a naturalized U.S. citizen in 2009. She was previously Dean of the School of Engineering and Applied Science at Princeton University.-Biography:Klawe was born in...
, and Kleitman
Daniel Kleitman
Daniel J. Kleitman is a professor of applied mathematics at MIT. His research interests include combinatorics, graph theory, genomics, and operations research.- Biography :...
; by Lubiw; and by Sack
Jörg-Rüdiger Sack
Jörg-Rüdiger Wolfgang Sack is a professor of computer science at Carleton University, where he holds the SUN–NSERC chair in Applied Parallel Computing. Sack received a masters degree from the University of Bonn in 1979 and a Ph.D. in 1984 from McGill University, under the supervision of Godfried...
and Toussaint
Godfried Toussaint
Godfried T. Toussaint is a Research Professor of Computer Science at New York University Abu Dhabi in Abu Dhabi, United Arab Emirates. He is an expert on various aspects of computational geometry, discrete geometry, and their applications: pattern recognition , motion planning, visualization ,...
.
A related problem asks for the number of guards to cover the exterior of an arbitrary polygon (the "Fortress Problem"):
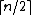 are sometimes necessary and always sufficient. In other words, the infinite exterior is more challenging to cover than the finite interior.
are sometimes necessary and always sufficient. In other words, the infinite exterior is more challenging to cover than the finite interior.Computational complexity
In decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
versions of the art gallery problem, one is given as input both a polygon and a number k, and must determine whether the polygon can be guarded with k or fewer guards. This problem and all of its standard variations (such as restricting the guard locations to vertices or edges of the polygon) are NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
.
Regarding approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s for the minimum number of guards, proved the problem to be APX-hard, implying that it is unlikely that any approximation ratio better than some fixed constant can be achieved by a polynomial time approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
. However, a constant approximation ratio is not known. Instead, a logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
ic approximation may be achieved for the minimum number of vertex guards by reducing the problem to a set cover problem. As showed, the set system derived from an art gallery problem has bounded VC dimension
VC dimension
In statistical learning theory, or sometimes computational learning theory, the VC dimension is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter...
, allowing the application of set cover algorithms based on ε-nets
Ε-net (computational geometry)
An ε-net is any of several related concepts in mathematics, and in particular in computational geometry, where it relates to the approximation of a general set by a collection of simpler subsets.- Background :...
whose approximation ratio is the logarithm of the optimal number of guards rather than of the number of polygon vertices.
For unrestricted guards, the infinite number of potential guard positions makes the problem even more difficult.
However, efficient algorithms are known for finding a set of at most
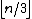 vertex guards, matching Chvátal's upper bound.
vertex guards, matching Chvátal's upper bound.proved that a placement for these guards may be computed in O(n log n) time in the worst case, via a divide and conquer algorithm
Divide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
.
gave a linear time algorithm by using Fisk's short proof and Bernard Chazelle
Bernard Chazelle
Bernard Chazelle is the Eugene Higgins Professor of Computer Science at Princeton University. Much of his work is in computational geometry, where he has found many of the best-known algorithms, such as linear-time triangulation of a simple polygon, as well as many useful complexity results, such...
's linear time plane triangulation algorithm.
An exact algorithm was proposed by for vertex guards. The authors conducted extensive computational experiments with several classes of polygons showing that optimal solutions can be found in relatively small computation times even for instances associated to thousands of vertices. The input data and the optimal solutions for these instances are available for download.
Three dimensions

Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
, then putting a guard at each vertex will not ensure that all of the museum is under observation. Although all of the surface of the polyhedron would be surveyed, for some polyhedra there are points in the interior which might not be under surveillance.

