
Sobolev conjugate
Encyclopedia
The Sobolev conjugate of p for 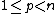 , where n is space dimensionality, is
, where n is space dimensionality, is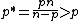
This is an important parameter in the Sobolev inequalities
.
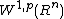 belongs to
belongs to 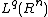 for some q>p. More specifically, when does
for some q>p. More specifically, when does 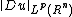 control
control 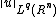 ? It is easy to check that
? It is easy to check that
the following inequality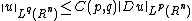 (*)
(*)
can not be true for arbitrary q. Consider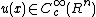 , infinitely differentiable function with compact support. Introduce
, infinitely differentiable function with compact support. Introduce  . We have that
. We have that
The inequality (*) for results in the following inequality for
results in the following inequality for 
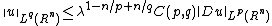
If , then by letting
, then by letting 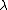 going to zero or infinity we obtain a contradiction. Thus the inequality (*) could only be true for
going to zero or infinity we obtain a contradiction. Thus the inequality (*) could only be true for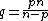 ,
,
which is the Sobolev conjugate.
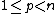 , where n is space dimensionality, is
, where n is space dimensionality, is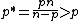
This is an important parameter in the Sobolev inequalities
Sobolev inequality
In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under...
.
Motivation
A question arises whether u from the Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
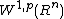 belongs to
belongs to 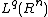 for some q>p. More specifically, when does
for some q>p. More specifically, when does 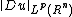 control
control 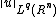 ? It is easy to check that
? It is easy to check thatthe following inequality
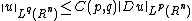 (*)
(*)can not be true for arbitrary q. Consider
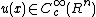 , infinitely differentiable function with compact support. Introduce
, infinitely differentiable function with compact support. Introduce 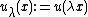 . We have that
. We have that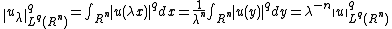
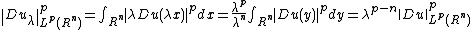
The inequality (*) for
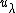 results in the following inequality for
results in the following inequality for 
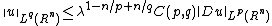
If
 , then by letting
, then by letting 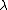 going to zero or infinity we obtain a contradiction. Thus the inequality (*) could only be true for
going to zero or infinity we obtain a contradiction. Thus the inequality (*) could only be true for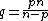 ,
,which is the Sobolev conjugate.

