Sinusoidal plane-wave solutions of the electromagnetic wave equation
Encyclopedia
Sinusoidal plane-wave solutions are particular solutions to the electromagnetic wave equation
.
The general solution of the electromagnetic wave equation
in homogeneous, linear, time-independent media can be written as a linear superposition
of plane-waves of different frequencies and polarizations.
The treatment in this article is classical
but, because of the generality of Maxwell's equations
for electrodynamics, the treatment can be converted into the quantum mechanical
treatment with only a reinterpretation of classical quantities (aside from the quantum mechanical treatment needed for charge and current densities).
The reinterpretation is based on the theories of Max Planck
and the interpretations by Albert Einstein
of those theories and of other experiments. The quantum generalization of the classical treatment can be found in the articles on Photon polarization
and Photon dynamics in the double-slit experiment
.
of frequencies and wavelengths associated with sinusoidal solutions of the wave equation. Polarizing filters can be used to decompose light into its various polarization components. The polarization components can be linear
, circular
or elliptical
.
solution for an electromagnetic wave
traveling in the z direction is (cgs units and SI units)

for the electric field and

for the magnetic field, where k is the wavenumber
,

is the angular frequency
of the wave, and is the speed of light
is the speed of light
. The hats on the vectors indicate unit vectors in the x, y, and z directions.
The plane wave is parameterized by the amplitude
s


and phases

where
 .
.
and
 .
.
.
The vector emerges from the plane-wave solution. The electric field solution can be rewritten in complex
notation as

where

is the Jones vector in the x-y plane. The notation for this vector is the bra-ket notation
of Dirac
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector.
given by
 .
.
 .
.

 are equal,
are equal,
 .
.
This represents a wave polarized at an angle with respect to the x axis. In that case the Jones vector can be written
with respect to the x axis. In that case the Jones vector can be written
 .
.
 is rotated by
is rotated by  radians with respect to
radians with respect to  the wave is circularly polarized
the wave is circularly polarized
. The Jones vector is

where the plus sign indicates right circular polarization and the minus sign indicates left circular polarization. In the case of circular polarization, the electric field vector of constant magnitude rotates in the x-y plane.
If unit vectors are defined such that

and

 then a circular polarization state can written in the "R-L basis" as
then a circular polarization state can written in the "R-L basis" as

where

and
 .
.
Any arbitrary state can be written in the R-L basis

where
 .
.
. The state vector is given by
 .
.
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
.
The general solution of the electromagnetic wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
in homogeneous, linear, time-independent media can be written as a linear superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of plane-waves of different frequencies and polarizations.
The treatment in this article is classical
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
but, because of the generality of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for electrodynamics, the treatment can be converted into the quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
treatment with only a reinterpretation of classical quantities (aside from the quantum mechanical treatment needed for charge and current densities).
The reinterpretation is based on the theories of Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
and the interpretations by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
of those theories and of other experiments. The quantum generalization of the classical treatment can be found in the articles on Photon polarization
Photon polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
and Photon dynamics in the double-slit experiment
Photon dynamics in the double-slit experiment
The dynamics of photons in the double-slit experiment describes the relationship between classical electromagnetic waves and photons, the quantum counterpart of classical electromagnetic waves, in the context of the double-slit experiment....
.
Explanation
Experimentally, every light signal can be decomposed into a spectrumElectromagnetic spectrum
The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....
of frequencies and wavelengths associated with sinusoidal solutions of the wave equation. Polarizing filters can be used to decompose light into its various polarization components. The polarization components can be linear
Linear polarization
In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation...
, circular
Circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
or elliptical
Elliptical polarization
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation...
.
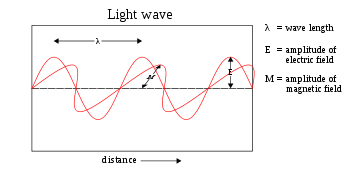
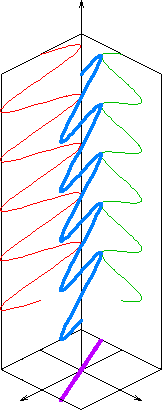
Plane waves
The plane sinusoidalSine wave
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields...
solution for an electromagnetic wave
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
traveling in the z direction is (cgs units and SI units)

for the electric field and

for the magnetic field, where k is the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
,

is the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of the wave, and
 is the speed of light
is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. The hats on the vectors indicate unit vectors in the x, y, and z directions.
The plane wave is parameterized by the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s



and phases
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...

where
 .
.and
 .
.Polarization state vector

Jones vector
All the polarization information can be reduced to a single vector, called the Jones vector, in the x-y plane. This vector, while arising from a purely classical treatment of polarization, can be interpreted as a quantum state vector. The connection with quantum mechanics is made in the article on photon polarizationPhoton polarization
Photon polarization is the quantum mechanical description of the classical polarized sinusoidal plane electromagnetic wave. Individual photons are completely polarized...
.
The vector emerges from the plane-wave solution. The electric field solution can be rewritten in complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
notation as

where

is the Jones vector in the x-y plane. The notation for this vector is the bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
of Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector.
Dual Jones vector
The Jones vector has a dualDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
given by
 .
.Normalization of the Jones vector
The Jones vector is normalized. The inner product of the vector with itself is .
.
Linear polarization
In general, the wave is linearly polarized when the phase angles are equal,
are equal, .
.This represents a wave polarized at an angle
 with respect to the x axis. In that case the Jones vector can be written
with respect to the x axis. In that case the Jones vector can be written .
.Circular polarization
If is rotated by
is rotated by  radians with respect to
radians with respect to  the wave is circularly polarized
the wave is circularly polarizedCircular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
. The Jones vector is

where the plus sign indicates right circular polarization and the minus sign indicates left circular polarization. In the case of circular polarization, the electric field vector of constant magnitude rotates in the x-y plane.
If unit vectors are defined such that

and



where

and
 .
.Any arbitrary state can be written in the R-L basis

where
 .
.Elliptical polarization
The general case in which the electric field rotates in the x-y plane and has variable magnitude is called elliptical polarizationElliptical polarization
In electrodynamics, elliptical polarization is the polarization of electromagnetic radiation such that the tip of the electric field vector describes an ellipse in any fixed plane intersecting, and normal to, the direction of propagation...
. The state vector is given by
 .
.See also
- Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
- Transverse modeTransverse modeA transverse mode of a beam of electromagnetic radiation is a particular electromagnetic field pattern of radiation measured in a plane perpendicular to the propagation direction of the beam...
- Theoretical and experimental justification for the Schrödinger equationTheoretical and experimental justification for the Schrödinger equationThe theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles...
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
- Mathematical descriptions of the electromagnetic fieldMathematical descriptions of the electromagnetic fieldThere are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental forces of nature. In this article four approaches are discussed.-Vector field approach:...
- Polarization from an atomic transition: linear and circular

