
Mathematical descriptions of the electromagnetic field
Encyclopedia
There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism
, one of the four fundamental forces of nature. In this article four approaches are discussed.
s called the electric field
and the magnetic field
. These vector fields each have a value defined at every point of space and time and are thus often regarded as functions of the space and time coordinates. As such, they are often written as (electric field) and (magnetic field).
If only the electric field
is non-zero, and is constant in time, the field is said to be an electrostatic field. Similarly, if only the magnetic field
is non-zero and is constant in time, the field is said to be a magnetostatic field. However, if either the electric or magnetic field has a time-dependence, then both fields must be considered together as a coupled electromagnetic field using Maxwell's equations
.
:
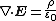 (Gauss' law)
(Gauss' law)
 (Gauss's law for magnetism)
(Gauss's law for magnetism)
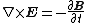 (Faraday's law
(Faraday's law
)
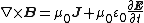 (Ampère–Maxwell law)
(Ampère–Maxwell law)
where is the charge density per unit volume, which can (and often does) depend on time and position, is the electric constant
, is the magnetic constant, and is the current per unit area, also a function of time and position. The units used above are the standard SI units.
Inside a linear material, Maxwell's equations change by switching the permeability and permittivity of free space with the permeability and permittivity of the linear material in question. Inside other materials which possess more complex responses to electromagnetic fields, these properties can be represented by tensors, with time-dependence related to the material's ability to respond to fast field changes (dispersion (optics)
, Green–Kubo relations), and possibly also field dependencies representing nonlinear and/or nonlocal material responses to large amplitude fields (nonlinear optics
).
The electric and magnetic fields transform under a Lorentz boost, a relativistic transformation of coordinates, in the direction as:
as:
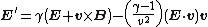
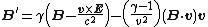
Component by component, for relative motion along the x-axis, this works out to be the following:


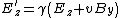

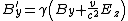

Finally, one thing worth noting is that if one of the fields is zero in one frame of reference, that doesn't necessarily mean it is zero in all other frames of reference. This can be seen by, for instance, making the unprimed electric field zero in the transformation to the primed electric field. In this case, depending on the orientation of the magnetic field, the primed system could see an electric field, even though there is none in the unprimed system.
It should be stressed when stating this that this does not mean two completely different sets of events are seen in the two frames, but that the same sequence of events is described in two different ways. The classic example, and the one cited in Einstein (1905), is that of a magnet and a conductor. If the conductor is held at rest, but the magnet moves, then there is a magnetic field which changes with time, which according to Faraday's Law
produces an electric field, which in turn causes a current to flow in the conductor. However, if the magnet is held stationary but the conductor moves, the charges in the conductor that are moving with the conductor as a whole form a kind of current, which produces a magnetic field which then causes current to flow. Assuming that in these cases, the object in motion in one of these cases has a velocity that is identical in speed but opposite in direction to the velocity of the object in motion in the other case, then the results are identical. A current, with the same strength, direction and electromotive force
, is induced in the conductor.
for the electric field, and the magnetic potential
for the magnetic field. The electric potential is a scalar field, while the magnetic potential is a vector field. This is why sometimes the electric potential is called the scalar potential and the magnetic potential is called the vector potential. These potentials can be used to find their associated fields as follows:
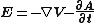
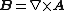
and Gauss's law for magnetism reduce to identities (i.e. in the case of Gauss's Law for magnetism, 0 = 0). The other two of Maxwell's equations don't turn out so simply.
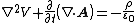 (Gauss's Law for electrostatics)
(Gauss's Law for electrostatics)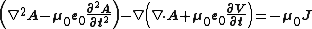 (Ampère-Maxwell Law)
(Ampère-Maxwell Law)
These equations taken together are as powerful and complete as Maxwell's equations. Moreover, the problem has been reduced somewhat, as between the electric and magnetic fields, each had three components which needed to be solved for, meaning it was necessary to solve for six quantities. In the potential formulation, there are only four quantities, the electric potential and the three components of the vector potential. However, this improvement is contrasted with the equations being much messier than Maxwell's equations using just the electric and magnetic fields.
Fortunately, there is a way to simplify these equations that takes advantage of the fact that the potential fields are not what is observed, the electric and magnetic fields are. Thus there is a freedom to impose conditions on the potentials so long as whatever condition is chosen to impose does not affect the resultant electric and magnetic fields. This freedom is called gauge freedom. Specifically for these equations, for any choice of a scalar function of position and time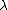 , the potentials can be changed as follows:
, the potentials can be changed as follows:
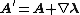
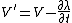
This freedom can be used to greatly simplify the potential formulation. Generally, two such scalar functions are chosen. The first is chosen in such a way that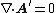 , which corresponds to the case of magnetostatics. In terms of
, which corresponds to the case of magnetostatics. In terms of 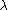 , this means that it must satisfy the equation
, this means that it must satisfy the equation 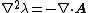 . This choice of function is generally called the Coulomb gauge, and results in the following formulation of Maxwell's equations:
. This choice of function is generally called the Coulomb gauge, and results in the following formulation of Maxwell's equations:
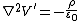
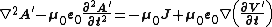
There are several things worth noting about Maxwell's equations in the Coulomb gauge. Firstly, solving for the electric potential is very easy, as the equation is a version of Poisson's equation
. Secondly, solving for the magnetic vector potential is particularly hard to calculate. This is the big disadvantage of this gauge. The third thing to note, and something which is not immediately obvious, is that the electric potential changes instantly everywhere in response to a change in conditions in one locality.
For instance, if a charge is moved in New York at 1 pm local time, then a hypothetical observer in Australia who could measure the electric potential directly would measure a change in the potential at 1 pm New York time. This seemingly goes against the prohibition in special relativity
of sending information, signals, or anything faster than the speed of light. The solution to this apparent problem lies in the fact that, as previously stated, no observers measure the potentials, they measure the electric and magnetic fields. So, the combination of and used in determining the electric field restores the speed limit imposed by special relativity for the electric field, making all observable quantities consistent with relativity.
The second scalar function that is used very often is called the Lorenz gauge. This gauge chooses the scalar function such that . This means
. This means 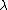 must satisfy the equation
must satisfy the equation 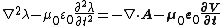 . The Lorenz gauge results in the following form of Maxwell's equations:
. The Lorenz gauge results in the following form of Maxwell's equations:
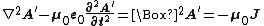
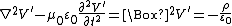
The operator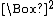 is called the d'Alembertian. These equations are inhomogenous versions of the wave equation
is called the d'Alembertian. These equations are inhomogenous versions of the wave equation
, with the terms on the right side of the equation serving as the source functions for the wave. These equations lead to two solutions: advanced potentials (which depend on the configuration of the sources at future points in time), and retarded potentials (which depend on the past configurations of the sources); the former are usually (and sensibly) dismissed as 'non-physical' in favor of the latter, which preserve causality.
It must be strongly emphasized that, as pointed out above, the Lorentz gauge is no more valid than any other gauge, as the potentials themselves are unobservable (with only a few loopholes, such as the Aharonov–Bohm effect, that still leave gauge invariance intact); any causality exhibited by the potentials will vanish for the observable fields, which are the physically meaningful quantities.
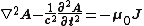
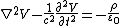
This is the basis for the extension of Maxwell equations to quantum electrodynamics, which yields the equations:
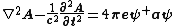
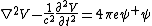
, or a bivector
, usually written as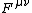 . This is called the electromagnetic field tensor, and it puts the electric and magnetic forces on the same footing. In matrix form, the tensor is as below.
. This is called the electromagnetic field tensor, and it puts the electric and magnetic forces on the same footing. In matrix form, the tensor is as below.

where
There is actually another way of merging the electric and magnetic fields into an antisymmetric tensor, by replacing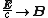 and
and 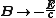 , to get the dual tensor
, to get the dual tensor 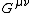 .
.
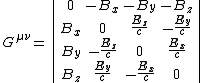
In the context of special relativity
, both of these transform according to the Lorentz transformation
like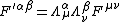 , where the
, where the  are the Lorentz transformation tensors for a given change in reference frame. Though there are two such tensors in the equation, they are the same tensor, just used in the summation differently.
are the Lorentz transformation tensors for a given change in reference frame. Though there are two such tensors in the equation, they are the same tensor, just used in the summation differently.
have the following form.
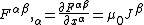
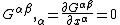
In the above, the tensor notation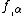 is used to denote partial derivatives,
is used to denote partial derivatives, 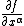 . The four-vector
. The four-vector 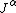 is called the current density four-vector
is called the current density four-vector
, which is the relativistic analogue to the charge density and current density. This four-vector is as follows.
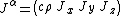
The first equation listed above corresponds to both Gauss's Law
( for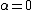 ) and the Ampère-Maxwell Law
) and the Ampère-Maxwell Law
( for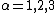 ). The second equation corresponds to the two remaining equations, Gauss's law for magnetism ( for
). The second equation corresponds to the two remaining equations, Gauss's law for magnetism ( for  ) and Faraday's Law
) and Faraday's Law
( for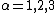 ).
).
This short form of writing Maxwell's equations illustrates an idea shared amongst some physicists, namely that the laws of physics take on a simpler form when written using tensors.
.
The most straightforward method of demonstrating the recovery of Maxwell's equations via the GA formalism is to descend from the Spacetime algebra
by selecting a timelike direction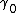 and then deal simply with the 3D spatial algebra (equivalent to the Pauli algebra). So we need to expand
and then deal simply with the 3D spatial algebra (equivalent to the Pauli algebra). So we need to expand
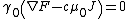
To do so first note that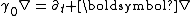
where a bold font is used for the spatial gradient.
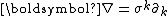
Similarly, multiplication of the four vector current density also has scalar and spatial vector components. With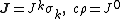 this is
this is
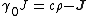
One obtains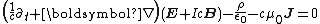
Noting that the pseudoscalar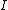 commutes with all spatial vectors, that
commutes with all spatial vectors, that 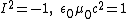 and
and 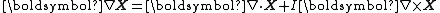 for spatial vectors
for spatial vectors 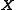 , one can expand and regroup this yielding
, one can expand and regroup this yielding
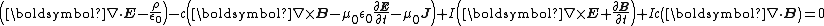
We have scalar, vector, bivector, and trivector grades. Equating each to zero recovers all of Maxwell's equations in their traditional vector form.
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, one of the four fundamental forces of nature. In this article four approaches are discussed.
Vector field approach
The most common description of the electromagnetic field to use two three-dimensional vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s called the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. These vector fields each have a value defined at every point of space and time and are thus often regarded as functions of the space and time coordinates. As such, they are often written as (electric field) and (magnetic field).
If only the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
is non-zero, and is constant in time, the field is said to be an electrostatic field. Similarly, if only the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
is non-zero and is constant in time, the field is said to be a magnetostatic field. However, if either the electric or magnetic field has a time-dependence, then both fields must be considered together as a coupled electromagnetic field using Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
.
Maxwell's equations in vector field approach
The behaviour of electric and magnetic fields, whether in cases of electrostatics, magnetostatics, or electrodynamics (electromagnetic fields), is governed in a vacuum by Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
:
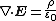 (Gauss' law)
(Gauss' law) (Gauss's law for magnetism)
(Gauss's law for magnetism)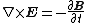 (Faraday's law
(Faraday's lawFaraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
)
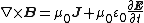 (Ampère–Maxwell law)
(Ampère–Maxwell law)where is the charge density per unit volume, which can (and often does) depend on time and position, is the electric constant
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
, is the magnetic constant, and is the current per unit area, also a function of time and position. The units used above are the standard SI units.
Inside a linear material, Maxwell's equations change by switching the permeability and permittivity of free space with the permeability and permittivity of the linear material in question. Inside other materials which possess more complex responses to electromagnetic fields, these properties can be represented by tensors, with time-dependence related to the material's ability to respond to fast field changes (dispersion (optics)
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
, Green–Kubo relations), and possibly also field dependencies representing nonlinear and/or nonlocal material responses to large amplitude fields (nonlinear optics
Nonlinear optics
Nonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
).
Relativistic transformation of fields in vector field approach
Maxwell's equations, when they were first stated in their complete form in 1865, would turn out to be compatible with special relativity. Moreover, the apparent coincidences in which the same effect was observed due to different physical phenomena by two different observers would be shown to be not coincidental in the least by special relativity. In fact, half of Einstein's 1905 first paper on special relativity, "On the Electrodynamics of Moving Bodies," explains how to transform Maxwell's equations.The electric and magnetic fields transform under a Lorentz boost, a relativistic transformation of coordinates, in the direction
 as:
as: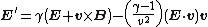
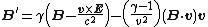
Component by component, for relative motion along the x-axis, this works out to be the following:


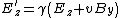

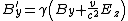

Finally, one thing worth noting is that if one of the fields is zero in one frame of reference, that doesn't necessarily mean it is zero in all other frames of reference. This can be seen by, for instance, making the unprimed electric field zero in the transformation to the primed electric field. In this case, depending on the orientation of the magnetic field, the primed system could see an electric field, even though there is none in the unprimed system.
It should be stressed when stating this that this does not mean two completely different sets of events are seen in the two frames, but that the same sequence of events is described in two different ways. The classic example, and the one cited in Einstein (1905), is that of a magnet and a conductor. If the conductor is held at rest, but the magnet moves, then there is a magnetic field which changes with time, which according to Faraday's Law
Faraday's law
Faraday's law may refer to the following:*Faraday's laws of electrolysis in chemistry*Faraday's law of induction, also known as Faraday-Lenz Law, in electromagnetism physics**The Maxwell–Faraday equation...
produces an electric field, which in turn causes a current to flow in the conductor. However, if the magnet is held stationary but the conductor moves, the charges in the conductor that are moving with the conductor as a whole form a kind of current, which produces a magnetic field which then causes current to flow. Assuming that in these cases, the object in motion in one of these cases has a velocity that is identical in speed but opposite in direction to the velocity of the object in motion in the other case, then the results are identical. A current, with the same strength, direction and electromotive force
Electromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
, is induced in the conductor.
Potential field approach
Many times in the use and calculation of electric and magnetic fields, the approach used first computes an associated potential: the electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
for the electric field, and the magnetic potential
Magnetic potential
The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
for the magnetic field. The electric potential is a scalar field, while the magnetic potential is a vector field. This is why sometimes the electric potential is called the scalar potential and the magnetic potential is called the vector potential. These potentials can be used to find their associated fields as follows:
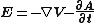
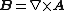
Maxwell's equation in potential formulation
These relations can be plugged into Maxwell's equations to find them in terms of the potentials. Faraday's lawFaraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
and Gauss's law for magnetism reduce to identities (i.e. in the case of Gauss's Law for magnetism, 0 = 0). The other two of Maxwell's equations don't turn out so simply.
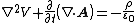 (Gauss's Law for electrostatics)
(Gauss's Law for electrostatics)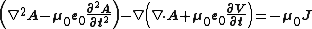 (Ampère-Maxwell Law)
(Ampère-Maxwell Law)These equations taken together are as powerful and complete as Maxwell's equations. Moreover, the problem has been reduced somewhat, as between the electric and magnetic fields, each had three components which needed to be solved for, meaning it was necessary to solve for six quantities. In the potential formulation, there are only four quantities, the electric potential and the three components of the vector potential. However, this improvement is contrasted with the equations being much messier than Maxwell's equations using just the electric and magnetic fields.
Fortunately, there is a way to simplify these equations that takes advantage of the fact that the potential fields are not what is observed, the electric and magnetic fields are. Thus there is a freedom to impose conditions on the potentials so long as whatever condition is chosen to impose does not affect the resultant electric and magnetic fields. This freedom is called gauge freedom. Specifically for these equations, for any choice of a scalar function of position and time
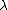 , the potentials can be changed as follows:
, the potentials can be changed as follows: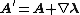
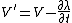
This freedom can be used to greatly simplify the potential formulation. Generally, two such scalar functions are chosen. The first is chosen in such a way that
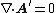 , which corresponds to the case of magnetostatics. In terms of
, which corresponds to the case of magnetostatics. In terms of 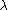 , this means that it must satisfy the equation
, this means that it must satisfy the equation 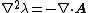 . This choice of function is generally called the Coulomb gauge, and results in the following formulation of Maxwell's equations:
. This choice of function is generally called the Coulomb gauge, and results in the following formulation of Maxwell's equations: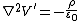
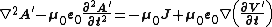
There are several things worth noting about Maxwell's equations in the Coulomb gauge. Firstly, solving for the electric potential is very easy, as the equation is a version of Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
. Secondly, solving for the magnetic vector potential is particularly hard to calculate. This is the big disadvantage of this gauge. The third thing to note, and something which is not immediately obvious, is that the electric potential changes instantly everywhere in response to a change in conditions in one locality.
For instance, if a charge is moved in New York at 1 pm local time, then a hypothetical observer in Australia who could measure the electric potential directly would measure a change in the potential at 1 pm New York time. This seemingly goes against the prohibition in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
of sending information, signals, or anything faster than the speed of light. The solution to this apparent problem lies in the fact that, as previously stated, no observers measure the potentials, they measure the electric and magnetic fields. So, the combination of and used in determining the electric field restores the speed limit imposed by special relativity for the electric field, making all observable quantities consistent with relativity.
The second scalar function that is used very often is called the Lorenz gauge. This gauge chooses the scalar function such that
 . This means
. This means 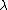 must satisfy the equation
must satisfy the equation 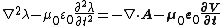 . The Lorenz gauge results in the following form of Maxwell's equations:
. The Lorenz gauge results in the following form of Maxwell's equations: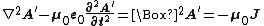
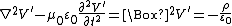
The operator
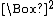 is called the d'Alembertian. These equations are inhomogenous versions of the wave equation
is called the d'Alembertian. These equations are inhomogenous versions of the wave equationWave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
, with the terms on the right side of the equation serving as the source functions for the wave. These equations lead to two solutions: advanced potentials (which depend on the configuration of the sources at future points in time), and retarded potentials (which depend on the past configurations of the sources); the former are usually (and sensibly) dismissed as 'non-physical' in favor of the latter, which preserve causality.
It must be strongly emphasized that, as pointed out above, the Lorentz gauge is no more valid than any other gauge, as the potentials themselves are unobservable (with only a few loopholes, such as the Aharonov–Bohm effect, that still leave gauge invariance intact); any causality exhibited by the potentials will vanish for the observable fields, which are the physically meaningful quantities.
Extension to quantum electrodynamics
The previous Lorentz Gauge equations, can also be written: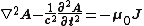
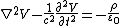
This is the basis for the extension of Maxwell equations to quantum electrodynamics, which yields the equations:
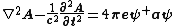
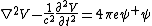
Tensor field approach
The electric and magnetic fields can be combined together mathematically to form an antisymmetric, second-rank tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, or a bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
, usually written as
 . This is called the electromagnetic field tensor, and it puts the electric and magnetic forces on the same footing. In matrix form, the tensor is as below.
. This is called the electromagnetic field tensor, and it puts the electric and magnetic forces on the same footing. In matrix form, the tensor is as below.
where
-
- E is the electric field
- B the magnetic field and
- c the speed of light. When using natural units, the speed of light is taken to equal 1.
There is actually another way of merging the electric and magnetic fields into an antisymmetric tensor, by replacing
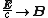 and
and 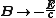 , to get the dual tensor
, to get the dual tensor 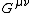 .
.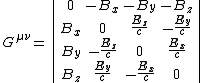
In the context of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, both of these transform according to the Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
like
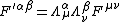 , where the
, where the  are the Lorentz transformation tensors for a given change in reference frame. Though there are two such tensors in the equation, they are the same tensor, just used in the summation differently.
are the Lorentz transformation tensors for a given change in reference frame. Though there are two such tensors in the equation, they are the same tensor, just used in the summation differently.Maxwell's equations in tensor notation
Using this tensor notation, Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
have the following form.
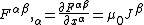
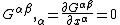
In the above, the tensor notation
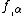 is used to denote partial derivatives,
is used to denote partial derivatives, 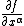 . The four-vector
. The four-vector 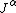 is called the current density four-vector
is called the current density four-vectorFour-current
In special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
, which is the relativistic analogue to the charge density and current density. This four-vector is as follows.
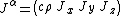
The first equation listed above corresponds to both Gauss's Law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
( for
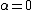 ) and the Ampère-Maxwell Law
) and the Ampère-Maxwell LawAmpère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
( for
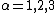 ). The second equation corresponds to the two remaining equations, Gauss's law for magnetism ( for
). The second equation corresponds to the two remaining equations, Gauss's law for magnetism ( for  ) and Faraday's Law
) and Faraday's LawFaraday's law
Faraday's law may refer to the following:*Faraday's laws of electrolysis in chemistry*Faraday's law of induction, also known as Faraday-Lenz Law, in electromagnetism physics**The Maxwell–Faraday equation...
( for
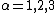 ).
).This short form of writing Maxwell's equations illustrates an idea shared amongst some physicists, namely that the laws of physics take on a simpler form when written using tensors.
Geometric algebra (GA) approach
This is the additional detail referred to in Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
.
The most straightforward method of demonstrating the recovery of Maxwell's equations via the GA formalism is to descend from the Spacetime algebra
Spacetime algebra
In mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
by selecting a timelike direction
 and then deal simply with the 3D spatial algebra (equivalent to the Pauli algebra). So we need to expand
and then deal simply with the 3D spatial algebra (equivalent to the Pauli algebra). So we need to expand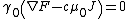
To do so first note that
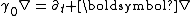
where a bold font is used for the spatial gradient.
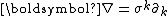
Similarly, multiplication of the four vector current density also has scalar and spatial vector components. With
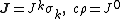 this is
this is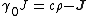
One obtains
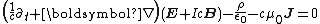
Noting that the pseudoscalar
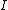 commutes with all spatial vectors, that
commutes with all spatial vectors, that 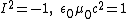 and
and 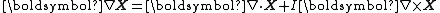 for spatial vectors
for spatial vectors 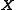 , one can expand and regroup this yielding
, one can expand and regroup this yielding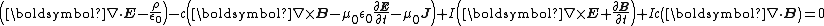
We have scalar, vector, bivector, and trivector grades. Equating each to zero recovers all of Maxwell's equations in their traditional vector form.
See also
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
- Speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
- Electric constantElectric constantThe physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
- Magnetic constant
- Free space
- Near and far fieldNear and far fieldThe near field and far field and the transition zone are regions of the electromagnetic radiation field that emanates from a transmitting antenna, or as a result of radiation scattering off an object...
- Electromagnetic fieldElectromagnetic fieldAn electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
- Electromagnetic fluxElectromagnetic fluxElectromagnetic flux may refer to one of the following:*Flux or flux density of electromagnetic radiation*Electric flux and magnetic flux....
- Quantum electrodynamicsQuantum electrodynamicsQuantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...

