
Shor's algorithm
Encyclopedia
Shor's algorithm, named after mathematician Peter Shor
, is a quantum algorithm
(an algorithm
which runs on a quantum computer
) for integer factorization
formulated in 1994. Informally it solves the following problem: Given an integer N, find its prime factor
s.
On a quantum computer, to factor an integer N, Shor's algorithm runs in polynomial time (the time taken is polynomial in log N, which is the size of the input). Specifically it takes time , demonstrating that the integer factorization problem can be efficiently solved on a quantum computer and is thus in the complexity class
BQP
. This is exponentially faster than the most efficient known classical factoring algorithm, the general number field sieve
, which works in sub-exponential time -- about (http://mathworld.wolfram.com/NumberFieldSieve.html). The efficiency lies in the efficiency of the quantum Fourier transform
, and modular exponentiation
by squarings
.
Given a quantum computer with a sufficient number of qubits, Shor's algorithm can be used to break public-key cryptography
schemes such as the widely used RSA scheme. RSA is based on the assumption that factoring large numbers is computationally infeasible. So far as is known, this assumption is valid for classical (non-quantum) computers; no classical algorithm is known that can factor in polynomial time. However, Shor's algorithm shows that factoring is efficient on a quantum computer, so an appropriately large quantum computer can break RSA. It was also a powerful motivator for the design and construction of quantum computers and for the study of new quantum computer algorithms. It has also facilitated research on new cryptosystems that are secure from quantum computers, collectively called post-quantum cryptography
.
In 2001, Shor's algorithm was demonstrated by a group at IBM, who factored 15 into 3 × 5, using an NMR implementation
of a quantum computer with 7 qubits.
However, some doubts have been raised as to whether IBM's experiment was a true demonstration of quantum computation, since no entanglement
was observed.
Since IBM's implementation, several other groups have implemented Shor's algorithm using photonic qubits, emphasizing that entanglement was observed.
 , find an integer
, find an integer 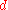 , strictly between 1 and
, strictly between 1 and  , that divides
, that divides  . We are interested in odd values of
. We are interested in odd values of  because any even value of
because any even value of  trivially has the number 2 as a prime factor. We can use a primality testing algorithm to make sure that
trivially has the number 2 as a prime factor. We can use a primality testing algorithm to make sure that  is indeed composite.
is indeed composite.
Moreover, for the algorithm to work, we need not to be the power of a prime. This can be tested by taking square, cubic, ...,
not to be the power of a prime. This can be tested by taking square, cubic, ..., 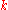 -roots of
-roots of  , for
, for 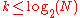 , and checking that none of these is an integer. (This actually excludes that
, and checking that none of these is an integer. (This actually excludes that 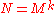 for some integer
for some integer  and
and  .)
.)
Since is not a power of a prime, it is the product of two coprime
is not a power of a prime, it is the product of two coprime
numbers greater than 1. As a consequence of the Chinese remainder theorem
, 1 has at least four distinct roots modulo
 , two of them being 1 and
, two of them being 1 and  . The aim of the algorithm is to find a square root
. The aim of the algorithm is to find a square root  of 1, other than 1 and
of 1, other than 1 and  ; such a
; such a  will lead to a factorization of
will lead to a factorization of  , as in other factoring algorithms
, as in other factoring algorithms
like the quadratic sieve
.
In turn, finding such a is reduced to finding an element
is reduced to finding an element  of even period with a certain additional property (as explained below, it is required that the condition of Step 6 of the classical part does not hold). The quantum algorithm is used for finding the period of randomly chosen elements
of even period with a certain additional property (as explained below, it is required that the condition of Step 6 of the classical part does not hold). The quantum algorithm is used for finding the period of randomly chosen elements  , as order-finding is a hard problem on a classical computer.
, as order-finding is a hard problem on a classical computer.
Shor's algorithm consists of two parts:
N. Given N, find Q = 2q such that , which implies
, which implies 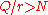 . The input and output qubit
. The input and output qubit
registers need to hold superpositions of values from 0 to Q − 1, and so have q qubits each. Using what might appear to be twice as many qubits as necessary guarantees that there are at least N different x which produce the same f(x), even as the period r approaches N/2.
Proceed as follows:
with N form a finite Abelian group
 under multiplication modulo
under multiplication modulo
N. The size is given by Euler's totient function
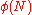 .
.
By the end of step 3, we have an integer a in this group. Since the group is finite, a must have a finite order r, the smallest positive integer such that

Therefore, N divides (also written | ) a r − 1 . Suppose we are able to obtain r, and it is even. (If r is odd, see step 5.) Now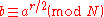 is a square root of 1 modulo
is a square root of 1 modulo  , different from 1. This is because
, different from 1. This is because  is the order of
is the order of  modulo
modulo  , so
, so  . If
. If 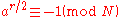 , by step 6 we have to restart the algorithm with a different random number
, by step 6 we have to restart the algorithm with a different random number  .
.
Eventually, we must hit an , of order
, of order  in
in  , such that
, such that 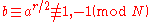 . This is because such a
. This is because such a  is a square root of 1 modulo
is a square root of 1 modulo  , other than 1 and
, other than 1 and  , whose existence is guaranteed by the Chinese remainder theorem, since
, whose existence is guaranteed by the Chinese remainder theorem, since  is not a prime power.
is not a prime power.
We claim that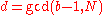 is a proper factor of
is a proper factor of  , that is,
, that is, 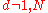 . In fact if
. In fact if  , then
, then  divides
divides  , so that
, so that  , against the construction of
, against the construction of  . If on the other hand
. If on the other hand 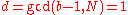 , then by Bézout's identity
, then by Bézout's identity
there are integers such that
such that .
.
Multiplying both sides by we obtain
we obtain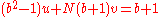 .
.
Since divides
divides  , we obtain that
, we obtain that  divides
divides  , so that
, so that  , again contradicting the construction of
, again contradicting the construction of  .
.
Thus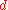 is the required proper factor of
is the required proper factor of  .
.
to be in many states simultaneously.
Physicists call this behavior a "superposition
" of states. To compute the period of a function f, we evaluate the function at all points simultaneously.
Quantum physics does not allow us to access all this information directly, though. A measurement
will yield only one of all possible values, destroying all others. But for the no cloning theorem
, we could first measure f(x) without measuring x, and then make a few copies of the resulting state (which is a superposition of states all having the same f(x)). Measuring x on these states would provide different x values which give the same f(x), leading to the period. Because we cannot make exact copies of a quantum state
, this method does not work. Therefore we have to carefully transform the superposition to another state that will return the correct answer with high probability. This is achieved by the quantum Fourier transform
.
Shor thus had to solve three "implementation" problems. All of them had to be implemented "fast", which means that they can be implemented with a number of quantum gate
s that is polynomial in .
.
After all these transformations a measurement will yield an approximation to the period r.
For simplicity assume that there is a y such that yr/Q is an integer.
Then the probability to measure y is 1.
To see that we notice that then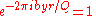
for all integers b. Therefore the sum whose square gives us the probability to measure y will be Q/r since b takes roughly Q/r values and thus the probability is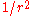 . There are r y such that yr/Q is an integer and also r possibilities for
. There are r y such that yr/Q is an integer and also r possibilities for 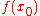 , so the probabilities sum to 1.
, so the probabilities sum to 1.
Note: another way to explain Shor's algorithm is by noting that it is just the quantum phase estimation algorithm
in disguise.
 , for some r, and we wish to compute r, which is the discrete logarithm
, for some r, and we wish to compute r, which is the discrete logarithm
: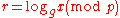 . Consider the Abelian group
. Consider the Abelian group 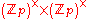 where each factor corresponds to modular multiplication of nonzero values, assuming p is prime. Now, consider the function
where each factor corresponds to modular multiplication of nonzero values, assuming p is prime. Now, consider the function
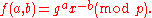
This gives us an Abelian hidden subgroup problem
, as f corresponds to a group homomorphism
. The kernel corresponds to modular multiples of (r,1). So, if we can find the kernel, we can find r
, the lead scientist, Dr. Nicholas Rush
, hoped to use Shor's algorithm to crack Destinys master code. He taught a quantum cryptography
class at the University of California, Berkeley
, in which Shor's algorithm was studied.
Shor's algorithm was also a correct answer to a question in a Physics Bowl competition on the television show The Big Bang Theory
.
Peter Shor
Peter Williston Shor is an American professor of applied mathematics at MIT, most famous for his work on quantum computation, in particular for devising Shor's algorithm, a quantum algorithm for factoring exponentially faster than the best currently-known algorithm running on a classical...
, is a quantum algorithm
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
(an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which runs on a quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
) for integer factorization
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
formulated in 1994. Informally it solves the following problem: Given an integer N, find its prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s.
On a quantum computer, to factor an integer N, Shor's algorithm runs in polynomial time (the time taken is polynomial in log N, which is the size of the input). Specifically it takes time , demonstrating that the integer factorization problem can be efficiently solved on a quantum computer and is thus in the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
BQP
BQP
In computational complexity theory BQP is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances...
. This is exponentially faster than the most efficient known classical factoring algorithm, the general number field sieve
General number field sieve
In number theory, the general number field sieve is the most efficient classical algorithm known for factoring integers larger than 100 digits...
, which works in sub-exponential time -- about (http://mathworld.wolfram.com/NumberFieldSieve.html). The efficiency lies in the efficiency of the quantum Fourier transform
Quantum Fourier transform
In quantum computing, the quantum Fourier transform is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform...
, and modular exponentiation
Modular exponentiation
Modular exponentiation is a type of exponentiation performed over a modulus. It is particularly useful in computer science, especially in the field of cryptography....
by squarings
Exponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
.
Given a quantum computer with a sufficient number of qubits, Shor's algorithm can be used to break public-key cryptography
Public-key cryptography
Public-key cryptography refers to a cryptographic system requiring two separate keys, one to lock or encrypt the plaintext, and one to unlock or decrypt the cyphertext. Neither key will do both functions. One of these keys is published or public and the other is kept private...
schemes such as the widely used RSA scheme. RSA is based on the assumption that factoring large numbers is computationally infeasible. So far as is known, this assumption is valid for classical (non-quantum) computers; no classical algorithm is known that can factor in polynomial time. However, Shor's algorithm shows that factoring is efficient on a quantum computer, so an appropriately large quantum computer can break RSA. It was also a powerful motivator for the design and construction of quantum computers and for the study of new quantum computer algorithms. It has also facilitated research on new cryptosystems that are secure from quantum computers, collectively called post-quantum cryptography
Post-quantum cryptography
Post-quantum cryptography refers to research on cryptographic primitives that are not breakable using quantum computers...
.
In 2001, Shor's algorithm was demonstrated by a group at IBM, who factored 15 into 3 × 5, using an NMR implementation
Nuclear magnetic resonance (NMR) quantum computing
NMR quantum computing uses the spin states of molecules as qubits. NMR differs from other implementations of quantum computers in that it uses an ensemble of systems, in this case molecules. The ensemble is initialized to be the thermal equilibrium state...
of a quantum computer with 7 qubits.
However, some doubts have been raised as to whether IBM's experiment was a true demonstration of quantum computation, since no entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
was observed.
Since IBM's implementation, several other groups have implemented Shor's algorithm using photonic qubits, emphasizing that entanglement was observed.
Procedure
The problem we are trying to solve is: given an odd composite numberComposite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
 , find an integer
, find an integer 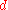 , strictly between 1 and
, strictly between 1 and  , that divides
, that divides  . We are interested in odd values of
. We are interested in odd values of  because any even value of
because any even value of  trivially has the number 2 as a prime factor. We can use a primality testing algorithm to make sure that
trivially has the number 2 as a prime factor. We can use a primality testing algorithm to make sure that  is indeed composite.
is indeed composite.Moreover, for the algorithm to work, we need
 not to be the power of a prime. This can be tested by taking square, cubic, ...,
not to be the power of a prime. This can be tested by taking square, cubic, ..., 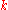 -roots of
-roots of  , for
, for 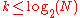 , and checking that none of these is an integer. (This actually excludes that
, and checking that none of these is an integer. (This actually excludes that 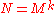 for some integer
for some integer  and
and  .)
.)Since
 is not a power of a prime, it is the product of two coprime
is not a power of a prime, it is the product of two coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
numbers greater than 1. As a consequence of the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, 1 has at least four distinct roots modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
 , two of them being 1 and
, two of them being 1 and  . The aim of the algorithm is to find a square root
. The aim of the algorithm is to find a square root  of 1, other than 1 and
of 1, other than 1 and  ; such a
; such a  will lead to a factorization of
will lead to a factorization of  , as in other factoring algorithms
, as in other factoring algorithmsInteger factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
like the quadratic sieve
Quadratic sieve
The quadratic sieve algorithm is a modern integer factorization algorithm and, in practice, the second fastest method known . It is still the fastest for integers under 100 decimal digits or so, and is considerably simpler than the number field sieve...
.
In turn, finding such a
 is reduced to finding an element
is reduced to finding an element  of even period with a certain additional property (as explained below, it is required that the condition of Step 6 of the classical part does not hold). The quantum algorithm is used for finding the period of randomly chosen elements
of even period with a certain additional property (as explained below, it is required that the condition of Step 6 of the classical part does not hold). The quantum algorithm is used for finding the period of randomly chosen elements  , as order-finding is a hard problem on a classical computer.
, as order-finding is a hard problem on a classical computer.Shor's algorithm consists of two parts:
- A reduction, which can be done on a classical computer, of the factoring problem to the problem of orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
-finding. - A quantum algorithm to solve the order-finding problem.
Classical part
- Pick a random number a < N
- Compute gcdGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(a, N). This may be done using the Euclidean algorithmEuclidean algorithmIn mathematics, the Euclidean algorithm is an efficient method for computing the greatest common divisor of two integers, also known as the greatest common factor or highest common factor...
. - If gcd(a, N) ≠ 1, then there is a nontrivialNontrivialNontrivial is the opposite of trivial. In contexts where trivial has a formal meaning, nontrivial is its antonym.It is a term common among communities of engineers and mathematicians, to indicate a statement or theorem that is not obvious or easy to prove.-Examples:*In mathematics, it is often...
factor of N, so we are done. - Otherwise, use the period-finding subroutine (below) to find r, the periodPeriodic functionIn mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
of the following function:
 ,
,
i.e. the orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
 of
of  in
in 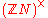 Multiplicative group of integers modulo nIn modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
Multiplicative group of integers modulo nIn modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
, which is the smallest positive integer r for which
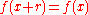
- If r is odd, go back to step 1.
- If a r /2 ≡ −1 (modModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
N), go back to step 1. - gcd(ar/2 ± 1, N) is a nontrivial factor of N. We are done.
Quantum part: Period-finding subroutine
The quantum circuits used for this algorithm are custom designed for each choice of N and the random a used in f(x) = ax modModulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
N. Given N, find Q = 2q such that
 , which implies
, which implies 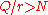 . The input and output qubit
. The input and output qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
registers need to hold superpositions of values from 0 to Q − 1, and so have q qubits each. Using what might appear to be twice as many qubits as necessary guarantees that there are at least N different x which produce the same f(x), even as the period r approaches N/2.
Proceed as follows:
- Initialize the registers to
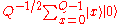
where x runs from 0 to Q − 1. This initial state is a superposition of Q states. - Construct f(x) as a quantum function and apply it to the above state, to obtain
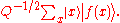
This is still a superposition of Q states.
- Apply the quantum Fourier transformQuantum Fourier transformIn quantum computing, the quantum Fourier transform is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform...
to the input register. This transform (operating on a superposition of power-of-two Q = 2q states)
uses a Qth root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
such as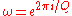 to distribute the amplitude of any given
to distribute the amplitude of any given  state equally among all Q of the
state equally among all Q of the 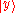 states, and to do so in a different way for each different x:
states, and to do so in a different way for each different x:
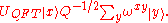
This leads to the final state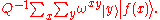
This is a superposition of many more than Q states, but many fewer than Q2 states. Although there are Q2 terms in the sum, the state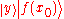 can be factored out whenever x0 and x produce the same value. Let
can be factored out whenever x0 and x produce the same value. Let be a Qth root of unity,
be a Qth root of unity,
- r be the period of f,
- x0 be the smallest of a set of x which yield the same given f(x) (we have x0 < r), and
- b run from 0 to
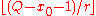 so that
so that 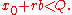
Then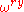 is a unit vector in the complex plane (
is a unit vector in the complex plane ( is a root of unity and r and y are integers), and the coefficient of
is a root of unity and r and y are integers), and the coefficient of 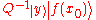 in the final state is
in the final state is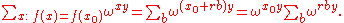
Each term in this sum represents a different path to the same result, and quantum interference occurs—constructive when the unit vectors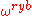 point in nearly the same direction in the complex plane, which requires that
point in nearly the same direction in the complex plane, which requires that 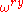 point along the positive real axis.
point along the positive real axis.
- Perform a measurement.
We obtain some outcome y in the input register and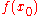 in the output register.
in the output register.
Since f is periodic, the probability of measuring some pair y and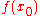 is given by
is given by
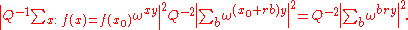
Analysis now shows that this probability is higher, the closer unit vector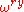 is to the positive real axis, or the closer yr/Q is to an integer. Unless r is a power of 2, it won't be a factor of Q.
is to the positive real axis, or the closer yr/Q is to an integer. Unless r is a power of 2, it won't be a factor of Q. - Perform Continued Fraction ExpansionContinued fractionIn mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
on y/Q to make an approximation of it, and produce some c/r′ by it that satisfies two conditions:- A: r′
- B: |y/Q - c/r′| < 1/2Q.
By satisfaction of these conditions, r′ would be the appropriate period r with high probability. - A: r′
- Check if f(x) = f(x + r′)

 If so, we are done.
If so, we are done. - Otherwise, obtain more candidates for r by using values near y, or multiples of r′. If any candidate works, we are done.
- Otherwise, go back to step 1 of the subroutine.
Explanation of the algorithm
The algorithm is composed of two parts. The first part of the algorithm turns the factoring problem into the problem of finding the period of a function, and may be implemented classically. The second part finds the period using the quantum Fourier transform, and is responsible for the quantum speedup.I. Obtaining factors from period
The integers less than N and coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
with N form a finite Abelian group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
 under multiplication modulo
under multiplication moduloModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
N. The size is given by Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
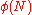 .
.By the end of step 3, we have an integer a in this group. Since the group is finite, a must have a finite order r, the smallest positive integer such that

Therefore, N divides (also written | ) a r − 1 . Suppose we are able to obtain r, and it is even. (If r is odd, see step 5.) Now
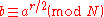 is a square root of 1 modulo
is a square root of 1 modulo  , different from 1. This is because
, different from 1. This is because  is the order of
is the order of  modulo
modulo  , so
, so  . If
. If 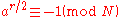 , by step 6 we have to restart the algorithm with a different random number
, by step 6 we have to restart the algorithm with a different random number  .
.Eventually, we must hit an
 , of order
, of order  in
in  , such that
, such that 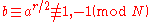 . This is because such a
. This is because such a  is a square root of 1 modulo
is a square root of 1 modulo  , other than 1 and
, other than 1 and  , whose existence is guaranteed by the Chinese remainder theorem, since
, whose existence is guaranteed by the Chinese remainder theorem, since  is not a prime power.
is not a prime power.We claim that
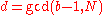 is a proper factor of
is a proper factor of  , that is,
, that is, 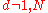 . In fact if
. In fact if  , then
, then  divides
divides  , so that
, so that  , against the construction of
, against the construction of  . If on the other hand
. If on the other hand 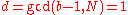 , then by Bézout's identity
, then by Bézout's identityBézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
there are integers
 such that
such that .
.Multiplying both sides by
 we obtain
we obtain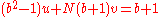 .
.Since
 divides
divides  , we obtain that
, we obtain that  divides
divides  , so that
, so that  , again contradicting the construction of
, again contradicting the construction of  .
.Thus
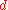 is the required proper factor of
is the required proper factor of  .
.II. Finding the period
Shor's period-finding algorithm relies heavily on the ability of a quantum computerQuantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
to be in many states simultaneously.
Physicists call this behavior a "superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
" of states. To compute the period of a function f, we evaluate the function at all points simultaneously.
Quantum physics does not allow us to access all this information directly, though. A measurement
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
will yield only one of all possible values, destroying all others. But for the no cloning theorem
No cloning theorem
The no-cloning theorem is a result of quantum mechanics that forbids the creation of identical copies of an arbitrary unknown quantum state. It was stated by Wootters, Zurek, and Dieks in 1982, and has profound implications in quantum computing and related fields.The state of one system can be...
, we could first measure f(x) without measuring x, and then make a few copies of the resulting state (which is a superposition of states all having the same f(x)). Measuring x on these states would provide different x values which give the same f(x), leading to the period. Because we cannot make exact copies of a quantum state
Quantum cloning
Quantum cloning is the process that takes an arbitrary, unknown quantum state and makes an exact copy without altering the original state in any way...
, this method does not work. Therefore we have to carefully transform the superposition to another state that will return the correct answer with high probability. This is achieved by the quantum Fourier transform
Quantum Fourier transform
In quantum computing, the quantum Fourier transform is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform...
.
Shor thus had to solve three "implementation" problems. All of them had to be implemented "fast", which means that they can be implemented with a number of quantum gate
Quantum gate
In quantum computing and specifically the quantum circuit model of computation, a quantum gate is a basic quantum circuit operating on a small number of qubits. They are the building blocks of quantum circuits, like classical logic gates are for conventional digital circuits.Unlike many classical...
s that is polynomial in
 .
.- Create a superposition of states.
This can be done by applying HadamardHadamard transformThe Hadamard transform is an example of a generalized class of Fourier transforms...
gates to all qubits in the input register. Another approach would be to use the quantum Fourier transform (see below).
- Implement the function f as a quantum transform.
To achieve this, Shor used repeated squaring for his modular exponentiation transformation. It is important to note that this step is more difficult to implement than the quantum Fourier transform, in that it requires ancillary qubits and substantially more gates to accomplish.
- Perform a quantum Fourier transform.
By using controlled rotation gates and Hadamard gates Shor designed a circuit for the quantum Fourier transform (with Q = 2q) that uses just gates.
gates.
After all these transformations a measurement will yield an approximation to the period r.
For simplicity assume that there is a y such that yr/Q is an integer.
Then the probability to measure y is 1.
To see that we notice that then
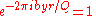
for all integers b. Therefore the sum whose square gives us the probability to measure y will be Q/r since b takes roughly Q/r values and thus the probability is
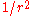 . There are r y such that yr/Q is an integer and also r possibilities for
. There are r y such that yr/Q is an integer and also r possibilities for 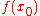 , so the probabilities sum to 1.
, so the probabilities sum to 1.Note: another way to explain Shor's algorithm is by noting that it is just the quantum phase estimation algorithm
Quantum phase estimation algorithm
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm that finds many applications as a subroutine in other algorithms...
in disguise.
Discrete logarithms
Suppose we know that , for some r, and we wish to compute r, which is the discrete logarithm
, for some r, and we wish to compute r, which is the discrete logarithmDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
:
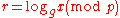 . Consider the Abelian group
. Consider the Abelian group 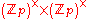 where each factor corresponds to modular multiplication of nonzero values, assuming p is prime. Now, consider the function
where each factor corresponds to modular multiplication of nonzero values, assuming p is prime. Now, consider the function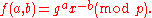
This gives us an Abelian hidden subgroup problem
Hidden subgroup problem
The hidden subgroup problem is a topic of research in mathematics and theoretical computer science.-Problem statement:Given a group G, a subgroup H ≤ G, and a set X, we say a function f : G → X hides the subgroup H if for all g1, g2 ∈ G,f = f if and only if g1H = g2H for the cosets of...
, as f corresponds to a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
. The kernel corresponds to modular multiples of (r,1). So, if we can find the kernel, we can find r
In popular culture
On the television show Stargate UniverseStargate Universe
Stargate Universe is a Canadian-American military science fiction television series and part of MGM's Stargate franchise. It follows the adventures of a present-day, multinational exploration team traveling on the Ancient spaceship Destiny many billions of light years distant from the Milky Way...
, the lead scientist, Dr. Nicholas Rush
Nicholas Rush
Dr. Nicholas Rush is a fictional character in the Canadian-American Metro-Goldwyn-Mayer-Syfy television series Stargate Universe, a military science fiction serial drama about the adventures of a present-day, multinational exploration team unable to return to Earth after an evacuation to the...
, hoped to use Shor's algorithm to crack Destinys master code. He taught a quantum cryptography
Quantum cryptography
Quantum key distribution uses quantum mechanics to guarantee secure communication. It enables two parties to produce a shared random secret key known only to them, which can then be used to encrypt and decrypt messages...
class at the University of California, Berkeley
University of California, Berkeley
The University of California, Berkeley , is a teaching and research university established in 1868 and located in Berkeley, California, USA...
, in which Shor's algorithm was studied.
Shor's algorithm was also a correct answer to a question in a Physics Bowl competition on the television show The Big Bang Theory
The Big Bang Theory
The Big Bang Theory is an American sitcom created by Chuck Lorre and Bill Prady, both of whom serve as executive producers on the show, along with Steven Molaro. All three also serve as head writers...
.
Further reading
.- Phillip Kaye, Raymond Laflamme, Michele Mosca, An introduction to quantum computing, Oxford University Press, 2007, ISBN 019857049X
- "Explanation for the man in the street" by Scott AaronsonScott AaronsonScott Joel Aaronson is a theoretical computer scientist and faculty member in the Electrical Engineering and Computer Science department at the Massachusetts Institute of Technology.-Education:...
, "approved" by Peter Shor. (Shor wrote "Great article, Scott! That’s the best job of explaining quantum computing to the man on the street that I’ve seen."). Scott Aaronson suggests the following 12 references as further reading (out of "the 10105000 quantum algorithm tutorials that are already on the web."):. Revised version of the original paper by Peter Shor ("28 pages, LaTeX. This is an expanded version of a paper that appeared in the Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, Nov. 20--22, 1994. Minor revisions made January, 1996"). - Quantum Computing and Shor's Algorithm, Matthew Hayward, 2005-02-17, imsa.edu, LaTeX2HTML version of the original 2750 line LaTeX document, also available as a 61 page PDF or postscript document.
- Quantum Computation and Shor's Factoring Algorithm, Ronald de Wolf, CWI and University of Amsterdam, January 12, 1999, 9 page postscript document.
- Shor's Factoring Algorithm, Notes from Lecture 9 of Berkeley CS 294-2, dated 4 Oct 2004, 7 page postscript document.
- Chapter 6 Quantum Computation, 91 page postscript document, Caltech, Preskill, PH229.
- Quantum computation: a tutorial by Samuel L. Braunstein.
- The Quantum States of Shor's Algorithm, by Neal Young, Last modified: Tue May 21 11:47:38 1996.
- A now-circular referenceCircular referenceA circular reference is a series of references where the last object references the first, resulting in a closed loop.-In language:A circular reference is not to be confused with the logical fallacy of a circular argument...
via the Wikipedia copy of this article; clearly Aaronson's link originally reached the February 20, 2007 version. - III. Breaking RSA Encryption with a Quantum Computer: Shor's Factoring Algorithm, Lecture notes on Quantum computation, Cornell University, Physics 481-681, CS 483; Spring, 2006 by N. David Mermin. Last revised 2006-03-28, 30 page PDF document.
- arXiv quant-ph/0303175 Shor's Algorithm for Factoring Large Integers. C. Lavor, L.R.U. Manssur, R. Portugal. Submitted on 29 Mar 2003. This work is a tutorial on Shor's factoring algorithm by means of a worked out example. Some basic concepts of Quantum Mechanics and quantum circuits are reviewed. It is intended for non-specialists which have basic knowledge on undergraduate Linear Algebra. 25 pages, 14 figures, introductory review.
- arXiv quant-ph/0010034 Shor's Quantum Factoring Algorithm, Samuel J. Lomonaco, Jr, Submitted October 9, 2000, This paper is a written version of a one hour lecture given on Peter Shor's quantum factoring algorithm. 22 pages.
- Chapter 20 Quantum Computation, from Computational Complexity: A Modern Approach, Draft of a book: Dated January 2007, Comments welcome!, Sanjeev Arora and Boaz Barak, Princeton University.
- A Step Toward Quantum Computing: Entangling 10 Billion Particles, from "Discover Magazine", Dated January 19, 2011.

