
Quantum phase estimation algorithm
Encyclopedia
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm
that finds many applications as a subroutine in other algorithms. The quantum phase estimation algorithm allows one to estimate the eigenphase of an eigenvector of a unitary gate, given access to a quantum state proportional to the eigenvector and a procedure to implement the unitary conditionally.
that operates on m qubits. Then all of the eigenvalues of U have absolute value 1. Thus the spectrum
of a unitary operator consists of phases . Given an eigenvector
. Given an eigenvector 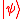 , such that
, such that 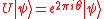 , the objective is to estimate
, the objective is to estimate  . The phase estimation algorithm solves this problem.
. The phase estimation algorithm solves this problem.
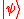 of
of  to a succession of n controlled operators, followed by the inverse of the quantum Fourier transform
to a succession of n controlled operators, followed by the inverse of the quantum Fourier transform
. The controlled operators are the powers of from
from  to controlled
to controlled 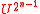 .
.
After putting the control lines into the Hadamard state, we have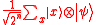 .
.
After the controlled application of , we have
, we have .
.
Applying the inverse of the quantum Fourier transform
upon the n qubits yields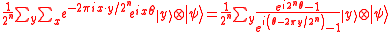 .
.
If the phase is exactly a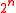 root of unity, the quantum Fourier transform will single out that phase in binary expansion. If
root of unity, the quantum Fourier transform will single out that phase in binary expansion. If
not, there will be a probability distribution clustered around the correct phase.
If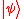 is really a superposition of eigenstates, there is a weighted probability distribution over the individual eigenstates, with the weight given by the Born probabilities. This is because eigenstates corresponding to different eigenvalues are orthogonal.
is really a superposition of eigenstates, there is a weighted probability distribution over the individual eigenstates, with the weight given by the Born probabilities. This is because eigenstates corresponding to different eigenvalues are orthogonal.
The efficiency of this algorithm depends on our access to . If we only have access via an oracle function, then we need exponentially many calls (in n) to the oracle to compute (for example)
. If we only have access via an oracle function, then we need exponentially many calls (in n) to the oracle to compute (for example) 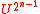 . If we have complete access to
. If we have complete access to  , then we can use exponentiation by squaring
, then we can use exponentiation by squaring
to compute the necessary powers of efficiently.
efficiently.
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
that finds many applications as a subroutine in other algorithms. The quantum phase estimation algorithm allows one to estimate the eigenphase of an eigenvector of a unitary gate, given access to a quantum state proportional to the eigenvector and a procedure to implement the unitary conditionally.
The Problem
Let U be a unitary operatorUnitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
that operates on m qubits. Then all of the eigenvalues of U have absolute value 1. Thus the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of a unitary operator consists of phases
 . Given an eigenvector
. Given an eigenvector 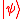 , such that
, such that 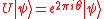 , the objective is to estimate
, the objective is to estimate  . The phase estimation algorithm solves this problem.
. The phase estimation algorithm solves this problem.The Algorithm
Suppose we wish to compute the phases to an accuracy of n bits. We achieve this by subjecting our eigenvector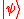 of
of  to a succession of n controlled operators, followed by the inverse of the quantum Fourier transform
to a succession of n controlled operators, followed by the inverse of the quantum Fourier transformQuantum Fourier transform
In quantum computing, the quantum Fourier transform is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform...
. The controlled operators are the powers of
 from
from  to controlled
to controlled 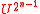 .
.After putting the control lines into the Hadamard state, we have
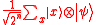 .
.After the controlled application of
 , we have
, we have .
.Applying the inverse of the quantum Fourier transform
Quantum Fourier transform
In quantum computing, the quantum Fourier transform is a linear transformation on quantum bits, and is the quantum analogue of the discrete Fourier transform...
upon the n qubits yields
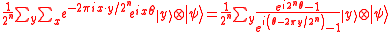 .
.If the phase is exactly a
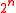 root of unity, the quantum Fourier transform will single out that phase in binary expansion. If
root of unity, the quantum Fourier transform will single out that phase in binary expansion. Ifnot, there will be a probability distribution clustered around the correct phase.
If
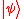 is really a superposition of eigenstates, there is a weighted probability distribution over the individual eigenstates, with the weight given by the Born probabilities. This is because eigenstates corresponding to different eigenvalues are orthogonal.
is really a superposition of eigenstates, there is a weighted probability distribution over the individual eigenstates, with the weight given by the Born probabilities. This is because eigenstates corresponding to different eigenvalues are orthogonal.The efficiency of this algorithm depends on our access to
 . If we only have access via an oracle function, then we need exponentially many calls (in n) to the oracle to compute (for example)
. If we only have access via an oracle function, then we need exponentially many calls (in n) to the oracle to compute (for example) 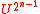 . If we have complete access to
. If we have complete access to  , then we can use exponentiation by squaring
, then we can use exponentiation by squaringExponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
to compute the necessary powers of
 efficiently.
efficiently.

