
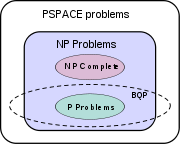
BQP
Encyclopedia
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
BQP (bounded error quantum polynomial time) is the class of decision problems solvable by a quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
in polynomial time, with an error probability of at most 1/3 for all instances. It is the quantum analogue of the complexity class BPP.
In other words, there is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for a quantum computer (a quantum algorithm
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
) that solves the decision problem with high probability and is guaranteed to run in polynomial time. On any given run of the algorithm, it has a probability of at most 1/3 that it will give the wrong answer.
Similarly to other "bounded error" probabilistic classes the choice of 1/3 in the definition is arbitrary. We can run the algorithm a constant number of times and take a majority vote to achieve any desired probability of correctness less than 1, using the Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
. Detailed analysis shows that the complexity class is unchanged by allowing error as high as 1/2 − n−c on the one hand, or requiring error as small as 2−nc on the other hand, where c is any positive constant, and n is the length of input.
Definition
BQP can also be viewed as a bounded-error uniform family of quantum circuitQuantum circuit
In quantum information theory, a quantum circuit is a model for quantum computation in which a computation is a sequence of quantum gates, which are reversible transformations on a quantum mechanical analog of an n-bit register...
s. A language L is in BQP if and only if there exists a polynomial-time uniform family of quantum circuits
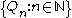 , such that
, such that
- For all
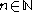 ,
, 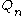 takes n qubits as input and outputs 1 bit
takes n qubits as input and outputs 1 bit - For all x in L,
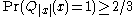
- For all x not in L,
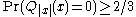
Quantum computation
The number of qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s in the computer is allowed to be a polynomial function of the instance size.
For example, algorithms are known for factoring an n-bit integer using just over 2n qubits (Shor's algorithm
Shor's algorithm
Shor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
).
Usually, computation on a quantum computer ends with a measurement
Measurement in quantum mechanics
The framework of quantum mechanics requires a careful definition of measurement. The issue of measurement lies at the heart of the problem of the interpretation of quantum mechanics, for which there is currently no consensus....
. This leads to a collapse
Wavefunction collapse
In quantum mechanics, wave function collapse is the phenomenon in which a wave function—initially in a superposition of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer...
of quantum state to one of the basis states. It can be said that the quantum state is measured to be in the correct state with high probability.
Quantum computers have gained widespread interest because some problems of practical interest are known to be in BQP, but suspected to be outside P. Some prominent examples are:
- Integer factorizationInteger factorizationIn number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
(see Shor's algorithmShor's algorithmShor's algorithm, named after mathematician Peter Shor, is a quantum algorithm for integer factorization formulated in 1994...
) - Discrete logarithmDiscrete logarithmIn mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
- Simulation of quantum systems (see universal quantum simulatorUniversal quantum simulatorA universal quantum simulator is a quantum computer proposed by Richard Feynman in 1982.Feynman showed that a classical Turing machine would presumably experience an exponential slowdown when simulating quantum phenomena, while his hypothetical universal quantum simulator would not. David Deutsch...
) - Computing the Jones polynomial at certain roots of unity
Relationship to other complexity classes
This class is defined for a quantum computer and its natural corresponding class for an ordinary computer (or a Turing machineTuring machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
plus a source of randomness) is BPP. Just like P and BPP, BQP is low for itself, which means BQPBQP = BQP. Informally, this is true because polynomial time algorithms are closed under composition. If a polynomial time algorithm calls as a subroutine polynomially many polynomial time algorithms, the resulting algorithm is still polynomial time.
BQP contains P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
and BPP and is contained in AWPP
Almost Wide Probabilistic Polynomial-Time
In theoretical computer science, Almost Wide Probabilistic Polynomial-Time is a complexity class for problems in the context of quantum computing....
, PP
PP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
and PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
.
In fact, BQP is low
Low (complexity)
In computational complexity theory, a complexity class B is said to be low for a complexity class A if AB = A; that is, A with an oracle for B is equal to A. Such a statement implies that an abstract machine which solves problems in A achieves no additional power if it is given the ability to solve...
for PP, meaning that a PP machine achieves no benefit from being able to solve BQP problems instantly, an indication of the possible difference in power between these similar classes.
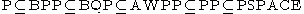
As the problem of P ≟ PSPACE has not yet been solved, the proof of inequality between BQP and classes mentioned above is supposed to be difficult. The relation between BQP and NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
is not known.
Adding postselection
Postselection
In probability theory, to postselect is to condition a probability space upon the occurrence of a given event. In symbols, once we postselect for an event E, the probability of some other event F changes from Pr[F] to the conditional probability Pr[F|E].For a discrete probability space, Pr[F|E] =...
to BQP results in the complexity class PostBQP
PostBQP
PostBQP is a complexity class consisting of all of the computational problems solvable in polynomial time on a quantum Turing machine with postselection and bounded error ....
which is equal to PP
PP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
.

