.gif)
Altitude (triangle)
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
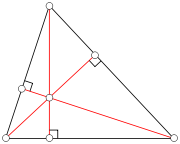
, an altitude of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
is a straight line through a vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
and perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to (i.e. forming a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
with) a line containing the base (the opposite side of the triangle). This line containing the opposite side is called the extended base of the altitude. The intersection between the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called the altitude, is the distance between the base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude of that vertex. It is a special case of orthogonal projection.
Altitudes can be used to compute the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of a triangle: one half of the product of an altitude's length and its base's length equals the triangle's area, as well as being related to the sides of the triangle through trigonometric functions.
In an isosceles triangle (a triangle with two congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
sides), the altitude having the incongruent side as its base will have the midpoint
Midpoint
The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
of that side as its foot. Also the altitude having the incongruent side as its base will form the angle bisector of the vertex.
In a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
, the altitude with the hypotenuse as base divides the hypotenuse into two lengths p and q. If we denote the length of the altitude by h, we then have the relation
- h2 = pq.
The orthocenter
The three altitudes intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle (and consequently the feet of the altitudes all fall on the triangle) if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the triangle is not obtuse (i.e. does not have an angle greater than a right angle). See also orthocentric system
Orthocentric system
In geometry, an orthocentric system is a set of four points in the plane one of which is the orthocenter of the triangle formed by the other three....
.
The orthocenter, along with the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
, circumcenter and center of the nine-point circle
Nine-point circle
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant points defined from the triangle...
all lie on a single line, known as the Euler line. The center of the nine-point circle lies at the midpoint
Midpoint
The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half that between the centroid and the orthocenter.
Unlike the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
and circumcenter of a triangle, the orthocenter has no special characteristics (such as being equidistant from all sides or vertices).
The isogonal conjugate
Isogonal conjugate
In geometry, the isogonal conjugate of a point P with respect to a triangle ABC is constructed by reflecting the lines PA, PB, and PC about the angle bisectors of A, B, and C. These three reflected lines concur at the isogonal conjugate of P...
and also the complement of the orthocenter is the circumcenter.
Four points in the plane such that one of them is the orthocenter of the triangle formed by the other three are called an orthocentric system
Orthocentric system
In geometry, an orthocentric system is a set of four points in the plane one of which is the orthocenter of the triangle formed by the other three....
or orthocentric quadrangle.
Let A, B, C denote the angles of the reference triangle, and let a = |BC|, b = |CA|, c = |AB| be the sidelengths. The orthocenter has trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
sec A : sec B : sec C and barycentric coordinates
Barycentric coordinates (mathematics)
In geometry, the barycentric coordinate system is a coordinate system in which the location of a point is specified as the center of mass, or barycenter, of masses placed at the vertices of a simplex . Barycentric coordinates are a form of homogeneous coordinates...
Orthic triangle
If the triangle ABC is oblique (not right-angled), the points of intersection of the altitudes with the sides of the triangles form another triangle, A'B'C', called the orthic triangle or altitude triangle. It is the pedal trianglePedal triangle
In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle.More specifically, consider a triangle ABC, and a point P that is not one of the vertices A, B, C. Drop perpendiculars from P to the three sides of the triangle...
of the orthocenter of the original triangle. Also, the incenter (that is, the center for the inscribed circle) of the orthic triangle is the orthocenter of the original triangle.
The orthic triangle is closely related to the tangential triangle, constructed as follows: let LA be the line tangent to the circumcircle of triangle ABC at vertex A, and define LB and LC analogously. Let A" = LB ∩ LC, B" = LC ∩ LA, C" = LC ∩ LA. The tangential triangle, A"B"C", is homothetic to the orthic triangle.
The orthic triangle provides the solution to Fagnano
Giulio Carlo de' Toschi di Fagnano
Giulio Carlo, Count Fagnano, and Marquis de Toschi was an Italian mathematician. He was probably the first to direct attention to the theory of elliptic integrals...
's problem which in 1775 asked for the minimum perimeter triangle inscribed in a given acute-angle triangle.
The orthic triangle of an acute triangle gives a triangular light route.
Trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
for the vertices of the orthic triangle are given by
- A' = 0 : sec B : sec C
- B' = sec A : 0 : sec C
- C' = sec A : sec B : 0
Trilinear coordinates
Trilinear coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative distances from the three sides of the triangle. Trilinear coordinates are an example of homogeneous coordinates...
for the vertices of the tangential triangle are given by
- A" = −a : b : c
- B" = a : −b : c
- C" = a : b : −c
Equilateral triangle theorem
For any point P within an equilateral triangle, the sum of the perpendiculars to the three sides is equal to the altitude of the triangle.Inradius theorems
Consider an arbitrary triangle with sides a, b, c and with correspondingaltitudes α, β, η. The altitudes and incircle radius r are related by
Let c, h, s be the sides of 3 squares associated with the right
triangle; the square on the hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
, and the triangle's 2 inscribed
squares respectively. The sides of these squares (c>h>s)
and the incircle radius r are related by a similar formula:
The symphonic theorem
In the case of the right triangle, the sides of the 3 squares c, h, s arerelated to each other by the symphonic theorem, as are the 3 altitudes α, β, η. The symphonic theorem states that triples (c2,h2,s2) and (α2,β2,η2) are harmonic, and that triples
 and
and  are Pythagorean:
are Pythagorean:Area theorem
Denoting the altitudes from sides a, b, and c respectively as ,
,  , and
, and  ,and denoting the semi-sum of the reciprocals of the altitudes as
,and denoting the semi-sum of the reciprocals of the altitudes as  we have
we have
External links
- Orthocenter of a triangle With interactive animation
- Animated demonstration of orthocenter construction Compass and straightedge.
- An interactive Java applet for the orthocenter
- Fagnano's Problem by Jay Warendorff, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
.





