
Representation theory of SU(2)
Encyclopedia
In the study of the representation theory
of Lie groups, the study of representations of SU(2) is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group
and a non-abelian group. The first condition implies the representation theory is discrete: representations are direct sums of a collection of basic irreducible representations (governed by the Peter–Weyl theorem
). The second means that irreducible representations will occur in dimensions greater than 1.
SU(2) is the universal covering group
of SO(3), and so its representation theory includes that of the latter.
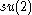 .
.
In principle this is the 'infinitesimal version' of SU(2); Lie algebras consist of infinitesimal transformation
s, and their Lie groups to 'integrated' transformations.
Then pass to the complex Lie algebra (i.e. complexify
the Lie algebra). This doesn't affect the representation theory. The Lie algebra is spanned by three elements e, f and h with the Lie brackets
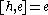
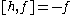
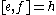
Since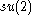 is semisimple, the representation ρ(h) is always diagonalizable (for complex number scalars). Its eigenvalues are called the weights
is semisimple, the representation ρ(h) is always diagonalizable (for complex number scalars). Its eigenvalues are called the weights
.
Suppose x is an eigenvector of the weight α. Then,
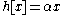
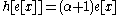
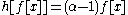
In other words, e raises the weight by one and f reduces the weight by one. A consequence is that
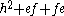
is a Casimir invariant
. By Schur's lemma
, its action is proportional to the identity map, for irreducible representations. The constant of proportionality is conveniently written
If x is an eigenvector of α, e[x]=0.
If the representation is irreducible,
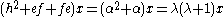
and so, since x is nonzero, α is either λ or −λ−1.
A lowest weight representation is a representation with a weight α which is lower than all the other weights.
If x is an eigenvector of α, f[x]=0.
If the rep is irreducible,
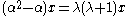
and so, α is either λ+1 or −λ.
Finite-dimensional representations only have finitely many weights, and so are both highest and lowest weight representations. For an irreducible finite-dimensional representation, the highest weight can't be less than the lowest weight. In addition, the difference between them has to be an integer because since
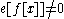
implies

and
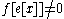
implies
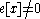 .
.
If the difference isn't an integer, there will always be a weight which is one more or one less than any given weight, contradicting the assumption of finite dimensionality.
Since λ < λ+1 and −λ−1 < −λ, without any loss of generality we can assume the highest weight is λ (if it's −λ−1, just redefine a new λ’ as −λ−1) and the lowest weight would then have to be −λ. This means λ has to be an integer or half-integer
. Every weight is a number between λ and −λ which differs from them by an integer and has multiplicity
one. This can be seen by assuming otherwise. Then, we can define a proper subrepresentation generated by an eigenvector of λ and f applied to it any number of times, contradicting the assumption of irreducibility.
This construction also shows for any given nonnegative integer multiple of half λ, all finite dimensional irreps with λ as its highest weight are equivalent (just make an identification of a highest weight eigenvector of one with one of the other).
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of Lie groups, the study of representations of SU(2) is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
and a non-abelian group. The first condition implies the representation theory is discrete: representations are direct sums of a collection of basic irreducible representations (governed by the Peter–Weyl theorem
Peter–Weyl theorem
In mathematics, the Peter–Weyl theorem is a basic result in the theory of harmonic analysis, applying to topological groups that are compact, but are not necessarily abelian. It was initially proved by Hermann Weyl, with his student Fritz Peter, in the setting of a compact topological group G...
). The second means that irreducible representations will occur in dimensions greater than 1.
SU(2) is the universal covering group
Universal covering group
In mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism...
of SO(3), and so its representation theory includes that of the latter.
Lie algebra representations
Consider first representations of the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
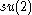 .
.In principle this is the 'infinitesimal version' of SU(2); Lie algebras consist of infinitesimal transformation
Infinitesimal transformation
In mathematics, an infinitesimal transformation is a limiting form of small transformation. For example one may talk about an infinitesimal rotation of a rigid body, in three-dimensional space. This is conventionally represented by a 3×3 skew-symmetric matrix A...
s, and their Lie groups to 'integrated' transformations.
Then pass to the complex Lie algebra (i.e. complexify
Complexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
the Lie algebra). This doesn't affect the representation theory. The Lie algebra is spanned by three elements e, f and h with the Lie brackets
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
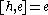
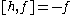
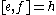
Since
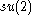 is semisimple, the representation ρ(h) is always diagonalizable (for complex number scalars). Its eigenvalues are called the weights
is semisimple, the representation ρ(h) is always diagonalizable (for complex number scalars). Its eigenvalues are called the weightsWeight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
.
Suppose x is an eigenvector of the weight α. Then,
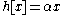
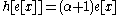
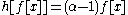
In other words, e raises the weight by one and f reduces the weight by one. A consequence is that
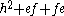
is a Casimir invariant
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
. By Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
, its action is proportional to the identity map, for irreducible representations. The constant of proportionality is conveniently written
- λ(λ+1).
Weights
A highest weight representation is a representation with a weight α which is greater than all the other weights.If x is an eigenvector of α, e[x]=0.
If the representation is irreducible,
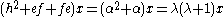
and so, since x is nonzero, α is either λ or −λ−1.
A lowest weight representation is a representation with a weight α which is lower than all the other weights.
If x is an eigenvector of α, f[x]=0.
If the rep is irreducible,
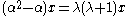
and so, α is either λ+1 or −λ.
Finite-dimensional representations only have finitely many weights, and so are both highest and lowest weight representations. For an irreducible finite-dimensional representation, the highest weight can't be less than the lowest weight. In addition, the difference between them has to be an integer because since
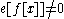
implies

and
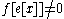
implies
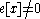 .
.If the difference isn't an integer, there will always be a weight which is one more or one less than any given weight, contradicting the assumption of finite dimensionality.
Since λ < λ+1 and −λ−1 < −λ, without any loss of generality we can assume the highest weight is λ (if it's −λ−1, just redefine a new λ’ as −λ−1) and the lowest weight would then have to be −λ. This means λ has to be an integer or half-integer
Half-integer
In mathematics, a half-integer is a number of the formn + 1/2,where n is an integer. For example,are all half-integers. Note that a half of an integer is not always a half-integer: half of an even integer is an integer but not a half-integer...
. Every weight is a number between λ and −λ which differs from them by an integer and has multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
one. This can be seen by assuming otherwise. Then, we can define a proper subrepresentation generated by an eigenvector of λ and f applied to it any number of times, contradicting the assumption of irreducibility.
This construction also shows for any given nonnegative integer multiple of half λ, all finite dimensional irreps with λ as its highest weight are equivalent (just make an identification of a highest weight eigenvector of one with one of the other).
See also
- spin (physics)Spin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
- Rotation operator (vector space)Rotation operator (vector space)This article derives the main properties of rotations in 3-dimensional space.The three Euler rotations are one way to bring a rigid object to any desired orientation by sequentially making rotations about axis' fixed relative to the object. However, this can also be achieved with one single...
- Rotation operator (quantum mechanics)
- representation theory of SL2(R)Representation theory of SL2(R)In mathematics, the main results concerning irreducible unitary representations of the Lie group SL are due to Gelfand and Naimark , V...

