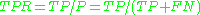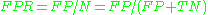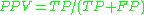Receiver operating characteristic
Encyclopedia
In signal detection theory, a receiver operating characteristic (ROC), or simply ROC curve, is a graphical
plot of the sensitivity, or true positive rate, vs. false positive rate (1 − specificity or 1 − true negative rate), for a binary classifier system as its discrimination threshold is varied. The ROC can also be represented equivalently by plotting the fraction of true positives out of the positives (TPR = true positive rate) vs. the fraction of false positives out of the negatives (FPR = false positive rate). Also known as a Relative Operating Characteristic curve, because it is a comparison of two operating characteristics (TPR & FPR) as the criterion changes.
ROC analysis provides tools to select possibly optimal models and to discard suboptimal ones independently from (and prior to specifying) the cost context or the class distribution. ROC analysis is related in a direct and natural way to cost/benefit analysis of diagnostic decision making
. The ROC curve was first developed by electrical engineers and radar engineers during World War II for detecting enemy objects in battle fields, also known as the signal detection theory, and was soon introduced in psychology
to account for perceptual detection of stimuli. ROC analysis since then has been used in medicine
, radiology
, biometrics
, and other areas for many decades, and is increasingly used in machine learning
and data mining
research.
A classification model (classifier or diagnosis
) is a mapping of instances into a certain class/group. The classifier or diagnosis result can be in a real value
(continuous output) in which the classifier boundary between classes must be determined by a threshold value, for instance to determine whether a person has hypertension
based on blood pressure
measure, or it can be in a discrete
class label indicating one of the classes.
Let us consider a two-class prediction problem (binary classification
), in which the outcomes are labeled either as positive (p) or negative (n) class. There are four possible outcomes from a binary classifier. If the outcome from a prediction is p and the actual value is also p, then it is called a true positive (TP); however if the actual value is n then it is said to be a false positive (FP). Conversely, a true negative (TN) has occurred when both the prediction outcome and the actual value are n, and false negative (FN) is when the prediction outcome is n while the actual value is p.
To get an appropriate example in a real-world problem, consider a diagnostic test that seeks to determine whether a person has a certain disease. A false positive in this case occurs when the person tests positive, but actually does not have the disease. A false negative, on the other hand, occurs when the person tests negative, suggesting they are healthy, when they actually do have the disease.
Let us define an experiment from P positive instances and N negative instances. The four outcomes can be formulated in a 2×2 contingency table
or confusion matrix
, as follows:
A ROC space is defined by FPR and TPR as x and y axes respectively, which depicts relative trade-offs between true positive (benefits) and false positive (costs). Since TPR is equivalent with sensitivity and FPR is equal to 1 − specificity, the ROC graph is sometimes called the sensitivity vs (1 − specificity) plot. Each prediction result or one instance of a confusion matrix represents one point in the ROC space.
The best possible prediction method would yield a point in the upper left corner or coordinate (0,1) of the ROC space, representing 100% sensitivity (no false negatives) and 100% specificity (no false positives). The (0,1) point is also called a perfect classification. A completely random guess
would give a point along a diagonal line (the so-called line of no-discrimination) from the left bottom to the top right corners. An intuitive example of random guessing is a decision by flipping coins (head or tail)
.
The diagonal divides the ROC space. Points above the diagonal represent good classification results, points below the line poor results. Note that the output of a poor predictor could simply be inverted to obtain points above the line.
Let us look into four prediction results from 100 positive and 100 negative instances:
TP=24
FP=88
112
FN=76
TN=12
88
100
100
200
TP=76
FP=12
88
FN=24
TN=88
112
100
100
200
TPR = 0.63
TPR = 0.77
TPR = 0.24
TPR = 0.76
FPR = 0.28
FPR = 0.77
FPR = 0.88
FPR = 0.12
ACC = 0.68
ACC = 0.50
ACC = 0.18
ACC = 0.82
Plots of the four results above in the ROC space are given in the figure. The result of method A clearly shows the best predictive power among A, B, and C. The result of B lies on the random guess line (the diagonal line), and it can be seen in the table that the accuracy of B is 50%. However, when C is mirrored across the center point (0.5,0.5), the resulting method C' is even better than A. This mirrored method simply reverses the predictions of whatever method or test produced the C contingency table. Although the original C method has negative predictive power, simply reversing its decisions leads to a new predictive method C' which has positive predictive power. When the C method predicts p or n, the C' method would predict n or p, respectively. In this manner, the C' test would perform the best. The closer a result from a contingency table is to the upper left corner, the better it predicts, but the distance from the random guess line in either direction is the best indicator of how much predictive power a method has. If the result is below the line (i.e. the method is worse than a random guess), all of the method's predictions must be reversed in order to utilize its power, thereby moving the result above the random guess line.
However, any attempt to summarize the ROC curve into a single number loses information about the pattern of tradeoffs of the particular discriminator algorithm.
, which plots the False Negative Rate (missed detections) vs. the False Positive Rate (false alarms), often on logarithmic scales.
The linearity of the zROC curve depends on the standard deviations of the target and lure strength distributions. If the standard deviations are equal, the slope will be 1.0. If the standard deviation of the target strength distribution is larger than the standard deviation of the lure strength distribution, then the slope will be smaller than 1.0. In most studies, it has been found that the zROC curve slopes constantly fall below 1, usually between 0.5 and 0.9. Many experiments yielded a zROC slope of 0.8. A slope of 0.8 implies that the variability of the target strength distribution is 25% larger than the variability of the lure strength distribution.
Another variable used is d'. d' is a measure of sensitivity for yes-no recognition that can easily be expressed in terms of z-values. d' measures sensitivity, in that it measures the degree of overlap between target and lure distributions. It is calculated as the mean of the target distribution minus the mean of the lure distribution, expressed in standard deviation units. For a given hit rate and false alarm rate, d' can be calculated with the following equation: d'=z(hit rate)- z(false alarm rate). Although d' is a commonly used parameter, it must be recognized that it is only relevant when strictly adhering to the very strong assumptions of strength theory made above.
The z-transformation of an ROC curve is always linear, as assumed, except in special situations. The Yonelinas Familiarity-Recollection model is a two-dimensional account of recognition memory. Instead of the subject simply answering yes or no to a specific input, the subject gives the input a feeling of familiarity, which operates like the original ROC curve. What changes, though, is a parameter for Recollection (R). Recollection is assumed to be all-or-none, and it trumps familiarity. If there were no recollection component, zROC would have a predicted slope of 1. However, when adding the recollection component, the zROC curve will be concave up, with a decreased slope. This difference in shape and slope result from an added element of variability due to some items being recollected. Patients with anterograde amnesia are unable to recollect, so their Yonelinas zROC curve would have a slope close to 1.0.
. The AUC is related to the Gini coefficient
(
) by the formula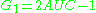 
, where:
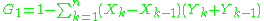
In this way, it is possible to calculate the AUC by using an average of a number of trapezoidal approximations.
The machine learning
community most often uses the ROC AUC statistic for model comparison. However, this practice has recently been questioned based upon new machine learning research that shows that the AUC is quite noisy as a classification measure and has some other significant problems in model comparison. A reliable and valid AUC estimate can be interpreted as the probability that the classifier will assign a higher score to a randomly chosen positive example than to a randomly chosen negative example. However, the critical research suggests frequent failures in obtaining reliable and valid AUC estimates. Thus, the practical value of the AUC measure has thus been called into question, raising the possibility that the AUC may actually introduce more uncertainty into machine learning classification accuracy comparisons than resolution.
, d'
is the most commonly used measure.
The illustration at the top right of the page shows the use of ROC graphs for the discrimination between the quality of different algorithms for predicting epitopes
. The graph shows that if one detects at least 60% of the epitopes in a virus
protein, at least 30% of the output is falsely marked as epitopes.
Sometimes it can be more useful to look at a specific region of the ROC Curve rather than at the whole curve. It is possible to compute partial AUC. For example, one could focus on the region of the curve with low false positive rate, which is often of prime interest for population screening tests.
Another common approach for classification problems in which P << N (common in bioinformatics applications) is to use a logarithmic scale for the x-axis.
for the analysis of radar signals
before it was employed in signal detection theory. Following the attack on Pearl Harbor
in 1941, the United States army began new research to increase the prediction of correctly detected Japanese aircraft from their radar signals.
In the 1950s, ROC curves were employed in psychophysics
to assess human (and occasionally non-human animal) detection of weak signals. In medicine
, ROC analysis has been extensively used in the evaluation of diagnostic tests. ROC curves are also used extensively in epidemiology
and medical research and are frequently mentioned in conjunction with evidence-based medicine
. In radiology
, ROC analysis is a common technique to evaluate new radiology techniques. In the social sciences, ROC analysis is often called the ROC Accuracy Ratio, a common technique for judging the accuracy of default probability models.
ROC curves also proved useful for the evaluation of machine learning
techniques. The first application of ROC in machine learning was by Spackman who demonstrated the value of ROC curves in comparing and evaluating different classification algorithm
s.
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
plot of the sensitivity, or true positive rate, vs. false positive rate (1 − specificity or 1 − true negative rate), for a binary classifier system as its discrimination threshold is varied. The ROC can also be represented equivalently by plotting the fraction of true positives out of the positives (TPR = true positive rate) vs. the fraction of false positives out of the negatives (FPR = false positive rate). Also known as a Relative Operating Characteristic curve, because it is a comparison of two operating characteristics (TPR & FPR) as the criterion changes.
ROC analysis provides tools to select possibly optimal models and to discard suboptimal ones independently from (and prior to specifying) the cost context or the class distribution. ROC analysis is related in a direct and natural way to cost/benefit analysis of diagnostic decision making
Decision making
Decision making can be regarded as the mental processes resulting in the selection of a course of action among several alternative scenarios. Every decision making process produces a final choice. The output can be an action or an opinion of choice.- Overview :Human performance in decision terms...
. The ROC curve was first developed by electrical engineers and radar engineers during World War II for detecting enemy objects in battle fields, also known as the signal detection theory, and was soon introduced in psychology
Psychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
to account for perceptual detection of stimuli. ROC analysis since then has been used in medicine
Medicine
Medicine is the science and art of healing. It encompasses a variety of health care practices evolved to maintain and restore health by the prevention and treatment of illness....
, radiology
Radiology
Radiology is a medical specialty that employs the use of imaging to both diagnose and treat disease visualized within the human body. Radiologists use an array of imaging technologies to diagnose or treat diseases...
, biometrics
Biometrics
Biometrics As Jain & Ross point out, "the term biometric authentication is perhaps more appropriate than biometrics since the latter has been historically used in the field of statistics to refer to the analysis of biological data [36]" . consists of methods...
, and other areas for many decades, and is increasingly used in machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
and data mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
research.
Basic concept
true positive (TP)
true negative (TN)
false positive (FP)
false negative (FN)
sensitivity or true positive rate (TPR)
false positive rate (FPR)
accuracy (ACC) 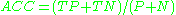 specificity (SPC) or True Negative Rate 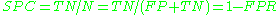 positive predictive value Positive predictive value In statistics and diagnostic testing, the positive predictive value, or precision rate is the proportion of subjects with positive test results who are correctly diagnosed. It is a critical measure of the performance of a diagnostic method, as it reflects the probability that a positive test... (PPV)
negative predictive value Negative predictive value In statistics and diagnostic testing, the negative predictive value is a summary statistic used to describe the performance of a diagnostic testing procedure. It is defined as the proportion of subjects with a negative test result who are correctly diagnosed. A high NPV means that when the test... (NPV) 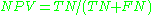 false discovery rate False discovery rate False discovery rate control is a statistical method used in multiple hypothesis testing to correct for multiple comparisons. In a list of rejected hypotheses, FDR controls the expected proportion of incorrectly rejected null hypotheses... (FDR) 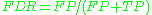 Matthews correlation coefficient Matthews Correlation Coefficient The Matthews correlation coefficient is used in machine learning as a measure of the quality of binary classifications. It takes into account true and false positives and negatives and is generally regarded as a balanced measure which can be used even if the classes are of very different sizes... (MCC) 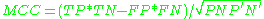 F1 score F1 Score In statistics, the F1 score is a measure of a test's accuracy. It considers both the precision p and the recall r of the test to compute the score: p is the number of correct results divided by the number of all returned results and r is the number of correct results divided by the number of... 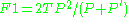 Source: Fawcett (2006). |
A classification model (classifier or diagnosis
Medical diagnosis
Medical diagnosis refers both to the process of attempting to determine or identify a possible disease or disorder , and to the opinion reached by this process...
) is a mapping of instances into a certain class/group. The classifier or diagnosis result can be in a real value
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
(continuous output) in which the classifier boundary between classes must be determined by a threshold value, for instance to determine whether a person has hypertension
Hypertension
Hypertension or high blood pressure is a cardiac chronic medical condition in which the systemic arterial blood pressure is elevated. What that means is that the heart is having to work harder than it should to pump the blood around the body. Blood pressure involves two measurements, systolic and...
based on blood pressure
Blood pressure
Blood pressure is the pressure exerted by circulating blood upon the walls of blood vessels, and is one of the principal vital signs. When used without further specification, "blood pressure" usually refers to the arterial pressure of the systemic circulation. During each heartbeat, BP varies...
measure, or it can be in a discrete
Countable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
class label indicating one of the classes.
Let us consider a two-class prediction problem (binary classification
Binary classification
Binary classification is the task of classifying the members of a given set of objects into two groups on the basis of whether they have some property or not. Some typical binary classification tasks are...
), in which the outcomes are labeled either as positive (p) or negative (n) class. There are four possible outcomes from a binary classifier. If the outcome from a prediction is p and the actual value is also p, then it is called a true positive (TP); however if the actual value is n then it is said to be a false positive (FP). Conversely, a true negative (TN) has occurred when both the prediction outcome and the actual value are n, and false negative (FN) is when the prediction outcome is n while the actual value is p.
To get an appropriate example in a real-world problem, consider a diagnostic test that seeks to determine whether a person has a certain disease. A false positive in this case occurs when the person tests positive, but actually does not have the disease. A false negative, on the other hand, occurs when the person tests negative, suggesting they are healthy, when they actually do have the disease.
Let us define an experiment from P positive instances and N negative instances. The four outcomes can be formulated in a 2×2 contingency table
Contingency table
In statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
or confusion matrix
Confusion matrix
In the field of artificial intelligence, a confusion matrix is a specific table layout that allows visualization of the performance of an algorithm, typically a supervised learning one . Each column of the matrix represents the instances in a predicted class, while each row represents the...
, as follows:
| actual value | ||||
|---|---|---|---|---|
| p | n | | total | ||
| prediction outcome |
p | True Positive |
False Positive |
P' |
| n | False Negative |
True Negative |
N' | |
| total | P | N | ||
ROC space
The contingency table can derive several evaluation "metrics" (see infobox). To draw an ROC curve, only the true positive rate (TPR) and false positive rate (FPR) are needed. TPR determines a classifier or a diagnostic test performance on classifying positive instances correctly among all positive samples available during the test. FPR, on the other hand, defines how many incorrect positive results occur among all negative samples available during the test.A ROC space is defined by FPR and TPR as x and y axes respectively, which depicts relative trade-offs between true positive (benefits) and false positive (costs). Since TPR is equivalent with sensitivity and FPR is equal to 1 − specificity, the ROC graph is sometimes called the sensitivity vs (1 − specificity) plot. Each prediction result or one instance of a confusion matrix represents one point in the ROC space.
The best possible prediction method would yield a point in the upper left corner or coordinate (0,1) of the ROC space, representing 100% sensitivity (no false negatives) and 100% specificity (no false positives). The (0,1) point is also called a perfect classification. A completely random guess
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
would give a point along a diagonal line (the so-called line of no-discrimination) from the left bottom to the top right corners. An intuitive example of random guessing is a decision by flipping coins (head or tail)
Coin flipping
Coin flipping or coin tossing or heads or tails is the practice of throwing a coin in the air to choose between two alternatives, sometimes to resolve a dispute between two parties...
.
The diagonal divides the ROC space. Points above the diagonal represent good classification results, points below the line poor results. Note that the output of a poor predictor could simply be inverted to obtain points above the line.
Let us look into four prediction results from 100 positive and 100 negative instances:
| A | B | C | C' | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
EWLINE
|
TP=77 | FP=77 | 154 | ||||||||||
| FN=23 | TN=23 | 46 | |||||||||||
| 100 | 100 | 200 |
Plots of the four results above in the ROC space are given in the figure. The result of method A clearly shows the best predictive power among A, B, and C. The result of B lies on the random guess line (the diagonal line), and it can be seen in the table that the accuracy of B is 50%. However, when C is mirrored across the center point (0.5,0.5), the resulting method C' is even better than A. This mirrored method simply reverses the predictions of whatever method or test produced the C contingency table. Although the original C method has negative predictive power, simply reversing its decisions leads to a new predictive method C' which has positive predictive power. When the C method predicts p or n, the C' method would predict n or p, respectively. In this manner, the C' test would perform the best. The closer a result from a contingency table is to the upper left corner, the better it predicts, but the distance from the random guess line in either direction is the best indicator of how much predictive power a method has. If the result is below the line (i.e. the method is worse than a random guess), all of the method's predictions must be reversed in order to utilize its power, thereby moving the result above the random guess line.
Curves in ROC space
Oftentimes, objects are classified based on a continuous random variable. For example, imagine that the protein level in diseased people and healthy people are normally distributed with means of 2 g/dL and 1 g/dL respectively. A medical test might measure the level of a certain protein in a blood sample and classify any number above a certain threshold as indicating disease. The experimenter can adjust the threshold (black vertical line in figure), which will in turn change the false positive rate. Increasing the threshold would result in fewer false positives, corresponding to a leftward movement on the curve. The actual shape of the curve is determined by how much overlap the two distributions have.Further interpretations
Sometimes, the ROC is used to generate a summary statistic. Common versions are:- the intercept of the ROC curve with the line at 90 degrees to the no-discrimination line (also called Youden's J statisticYouden's J statisticYouden's J statistic is a single statistic that captures the performance of a diagnostic test. The use of such a single index is "not generally to be recommended". It is equal to the risk difference for a dichotomous test ....
) - the area between the ROC curve and the no-discrimination line
- the area under the ROC curve, or "AUC" ("Area Under Curve"), or A'
- d'D'The sensitivity index or d' is a statistic used in signal detection theory. It provides the separation between the means of the signal and the noise distributions, in units of the standard deviation of the noise distribution....
, the distance between the mean of the distribution of activity in the system under noise-alone conditions and its distribution under signal-alone conditions, divided by their standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
, under the assumption that both these distributions are normal with the same standard deviation. Under these assumptions, it can be proved that the shape of the ROC depends only on d'D'The sensitivity index or d' is a statistic used in signal detection theory. It provides the separation between the means of the signal and the noise distributions, in units of the standard deviation of the noise distribution....
.
However, any attempt to summarize the ROC curve into a single number loses information about the pattern of tradeoffs of the particular discriminator algorithm.
Detection Error Tradeoff graph
An alternative to the ROC curve is the Detection Error Tradeoff (DET) graphDetection Error Tradeoff
A detection error tradeoff graph is a graphical plot of error rates for binary classification systems, plotting false reject rate vs. false accept rate...
, which plots the False Negative Rate (missed detections) vs. the False Positive Rate (false alarms), often on logarithmic scales.
Z-transformation
If a z-transformation is applied to the ROC curve, the curve will be transformed into a straight line. This z-transformation is based on a normal distribution with a mean of zero and a standard deviation of one. In strength theory, one must assume that the zROC is not only linear, but has a slope of 1.0. The normal distributions of target and lures is the factor causing the zROC to be linear.The linearity of the zROC curve depends on the standard deviations of the target and lure strength distributions. If the standard deviations are equal, the slope will be 1.0. If the standard deviation of the target strength distribution is larger than the standard deviation of the lure strength distribution, then the slope will be smaller than 1.0. In most studies, it has been found that the zROC curve slopes constantly fall below 1, usually between 0.5 and 0.9. Many experiments yielded a zROC slope of 0.8. A slope of 0.8 implies that the variability of the target strength distribution is 25% larger than the variability of the lure strength distribution.
Another variable used is d'. d' is a measure of sensitivity for yes-no recognition that can easily be expressed in terms of z-values. d' measures sensitivity, in that it measures the degree of overlap between target and lure distributions. It is calculated as the mean of the target distribution minus the mean of the lure distribution, expressed in standard deviation units. For a given hit rate and false alarm rate, d' can be calculated with the following equation: d'=z(hit rate)- z(false alarm rate). Although d' is a commonly used parameter, it must be recognized that it is only relevant when strictly adhering to the very strong assumptions of strength theory made above.
The z-transformation of an ROC curve is always linear, as assumed, except in special situations. The Yonelinas Familiarity-Recollection model is a two-dimensional account of recognition memory. Instead of the subject simply answering yes or no to a specific input, the subject gives the input a feeling of familiarity, which operates like the original ROC curve. What changes, though, is a parameter for Recollection (R). Recollection is assumed to be all-or-none, and it trumps familiarity. If there were no recollection component, zROC would have a predicted slope of 1. However, when adding the recollection component, the zROC curve will be concave up, with a decreased slope. This difference in shape and slope result from an added element of variability due to some items being recollected. Patients with anterograde amnesia are unable to recollect, so their Yonelinas zROC curve would have a slope close to 1.0.
Area Under Curve
The Area Under Curve (AUC) is equal to the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one. It can be shown that the area under the ROC curve is closely related to the Mann–Whitney U, which tests whether positives are ranked higher than negatives. It is also equivalent to the Wilcoxon test of ranksWilcoxon signed-rank test
The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used when comparing two related samples or repeated measurements on a single sample to assess whether their population mean ranks differ The Wilcoxon signed-rank test is a non-parametric statistical hypothesis test used...
. The AUC is related to the Gini coefficient
Gini coefficient
The Gini coefficient is a measure of statistical dispersion developed by the Italian statistician and sociologist Corrado Gini and published in his 1912 paper "Variability and Mutability" ....
(
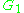) by the formula 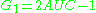, where: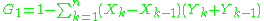In this way, it is possible to calculate the AUC by using an average of a number of trapezoidal approximations.
The machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
community most often uses the ROC AUC statistic for model comparison. However, this practice has recently been questioned based upon new machine learning research that shows that the AUC is quite noisy as a classification measure and has some other significant problems in model comparison. A reliable and valid AUC estimate can be interpreted as the probability that the classifier will assign a higher score to a randomly chosen positive example than to a randomly chosen negative example. However, the critical research suggests frequent failures in obtaining reliable and valid AUC estimates. Thus, the practical value of the AUC measure has thus been called into question, raising the possibility that the AUC may actually introduce more uncertainty into machine learning classification accuracy comparisons than resolution.
Other measures
In engineering, the area between the ROC curve and the no-discrimination line is often preferred, due to its useful mathematical properties as a non-parametric statistic. This area is often simply known as the discrimination. In psychophysicsPsychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they effect. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, more completely, as "the analysis of perceptual...
, d'
D'
The sensitivity index or d' is a statistic used in signal detection theory. It provides the separation between the means of the signal and the noise distributions, in units of the standard deviation of the noise distribution....
is the most commonly used measure.
The illustration at the top right of the page shows the use of ROC graphs for the discrimination between the quality of different algorithms for predicting epitopes
Epitope
An epitope, also known as antigenic determinant, is the part of an antigen that is recognized by the immune system, specifically by antibodies, B cells, or T cells. The part of an antibody that recognizes the epitope is called a paratope...
. The graph shows that if one detects at least 60% of the epitopes in a virus
Virus
A virus is a small infectious agent that can replicate only inside the living cells of organisms. Viruses infect all types of organisms, from animals and plants to bacteria and archaea...
protein, at least 30% of the output is falsely marked as epitopes.
Sometimes it can be more useful to look at a specific region of the ROC Curve rather than at the whole curve. It is possible to compute partial AUC. For example, one could focus on the region of the curve with low false positive rate, which is often of prime interest for population screening tests.
Another common approach for classification problems in which P << N (common in bioinformatics applications) is to use a logarithmic scale for the x-axis.
History
The ROC curve was first used during World War IIWorld War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
for the analysis of radar signals
Radar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
before it was employed in signal detection theory. Following the attack on Pearl Harbor
Attack on Pearl Harbor
The attack on Pearl Harbor was a surprise military strike conducted by the Imperial Japanese Navy against the United States naval base at Pearl Harbor, Hawaii, on the morning of December 7, 1941...
in 1941, the United States army began new research to increase the prediction of correctly detected Japanese aircraft from their radar signals.
In the 1950s, ROC curves were employed in psychophysics
Psychophysics
Psychophysics quantitatively investigates the relationship between physical stimuli and the sensations and perceptions they effect. Psychophysics has been described as "the scientific study of the relation between stimulus and sensation" or, more completely, as "the analysis of perceptual...
to assess human (and occasionally non-human animal) detection of weak signals. In medicine
Medicine
Medicine is the science and art of healing. It encompasses a variety of health care practices evolved to maintain and restore health by the prevention and treatment of illness....
, ROC analysis has been extensively used in the evaluation of diagnostic tests. ROC curves are also used extensively in epidemiology
Epidemiology
Epidemiology is the study of health-event, health-characteristic, or health-determinant patterns in a population. It is the cornerstone method of public health research, and helps inform policy decisions and evidence-based medicine by identifying risk factors for disease and targets for preventive...
and medical research and are frequently mentioned in conjunction with evidence-based medicine
Evidence-based medicine
Evidence-based medicine or evidence-based practice aims to apply the best available evidence gained from the scientific method to clinical decision making. It seeks to assess the strength of evidence of the risks and benefits of treatments and diagnostic tests...
. In radiology
Radiology
Radiology is a medical specialty that employs the use of imaging to both diagnose and treat disease visualized within the human body. Radiologists use an array of imaging technologies to diagnose or treat diseases...
, ROC analysis is a common technique to evaluate new radiology techniques. In the social sciences, ROC analysis is often called the ROC Accuracy Ratio, a common technique for judging the accuracy of default probability models.
ROC curves also proved useful for the evaluation of machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
techniques. The first application of ROC in machine learning was by Spackman who demonstrated the value of ROC curves in comparing and evaluating different classification algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s.
See also
- Constant false alarm rateConstant false alarm rateConstant false alarm rate detection refers to a common form of adaptive algorithm used in radar systems to detect target returns against a background of noise, clutter and interference.Other detection algorithms are not adaptive...
- Detection Error TradeoffDetection Error TradeoffA detection error tradeoff graph is a graphical plot of error rates for binary classification systems, plotting false reject rate vs. false accept rate...
- Detection theoryDetection theoryDetection theory, or signal detection theory, is a means to quantify the ability to discern between information-bearing energy patterns and random energy patterns that distract from the information Detection theory, or signal detection theory, is a means to quantify the ability to discern between...
- Expected performance curve
- False alarmFalse alarmA false alarm, also called a nuisance alarm, is the fake report of an emergency, causing unnecessary panic and/or bringing resources to a place where they are not needed. Over time, repeated false alarms in a certain area may cause occupants to start to ignore all alarms, knowing that each time it...
- Gain (information retrieval)Gain (information retrieval)The gain, also called improvement over random can be specified for a classifier and is an important measure to describe the performance of it.- Definition :...
- Precision and recallPrecision and recallIn pattern recognition and information retrieval, precision is the fraction of retrieved instances that are relevant, while recall is the fraction of relevant instances that are retrieved. Both precision and recall are therefore based on an understanding and measure of relevance...
Further reading
- Fawcett, Tom (2004) ROC Graphs: Notes and Practical Considerations for Researchers; Machine Learning, 2004
- Zou, K.H., O'Malley, A.J., Mauri, L. (2007). Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models. Circulation, 6;115(5):654–7.
- Lasko, T.A., J.G. Bhagwat, K.H. Zou and Ohno-Machado, L. (2005). The use of receiver operating characteristic curves in biomedical informatics. Journal of Biomedical Informatics, 38(5):404–415.
- Balakrishnan, N., (1991) Handbook of the Logistic Distribution, Marcel Dekker, Inc., ISBN 978-0-8247-8587-1.
- Gonen M., (2007) Analyzing Receiver Operating Characteristic Curves Using SAS, SAS Press, ISBN 978-1-59994-298-1.
- Green, W.H., (2003) Econometric Analysis, fifth edition, Prentice HallPrentice HallPrentice Hall is a major educational publisher. It is an imprint of Pearson Education, Inc., based in Upper Saddle River, New Jersey, USA. Prentice Hall publishes print and digital content for the 6-12 and higher-education market. Prentice Hall distributes its technical titles through the Safari...
, ISBN 0-13-066189-9. - Heagerty, P.J., Lumley, T., Pepe, M. S. (2000) Time-dependent ROC Curves for Censored Survival Data and a Diagnostic Marker Biometrics, 56:337 – 344
- Hosmer, D.W. and Lemeshow, S., (2000) Applied Logistic Regression, 2nd ed., New York; Chichester, WileyJohn Wiley & SonsJohn Wiley & Sons, Inc., also referred to as Wiley, is a global publishing company that specializes in academic publishing and markets its products to professionals and consumers, students and instructors in higher education, and researchers and practitioners in scientific, technical, medical, and...
, ISBN 0-471-35632-8. - Brown, C.D., and Davis, H.T. (2006) Receiver operating characteristic curves and related decision measures: a tutorial, Chemometrics and Intelligent Laboratory Systems, 80:24–38
- Mason, S.J. and Graham, N.E. (2002) Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q.J.R. Meteorol. Soc., 128:2145–2166.
- Pepe, M.S. (2003). The statistical evaluation of medical tests for classification and prediction. OxfordOxford University PressOxford University Press is the largest university press in the world. It is a department of the University of Oxford and is governed by a group of 15 academics appointed by the Vice-Chancellor known as the Delegates of the Press. They are headed by the Secretary to the Delegates, who serves as...
. ISBN 0198565828. - Carsten, S. Wesseling, S., Schink, T., and Jung, K. (2003) Comparison of Eight Computer Programs for Receiver-Operating Characteristic Analysis. Clinical Chemistry, 49:433–439
- Swets, J.A. (1995). Signal detection theory and ROC analysis in psychology and diagnostics: Collected papers. Lawrence Erlbaum Associates.
- Swets, J.A., Dawes, R., and Monahan, J. (2000) Better Decisions through Science. Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, October, pages 82–87.
External links
- Kelly H. Zou's bibliography of ROC literature and articles
- A more thorough treatment of ROC curves and signal detection theory
- Tom Fawcett's ROC Convex Hull: tutorial, program and papers
- Peter Flach's tutorial on ROC analysis in machine learning
- The magnificent ROC – An explanation and interactive demonstration of the connection of ROCs to archetypal bi-normal test result plots
- Web-based calculator for ROC Curves – by John Eng
- Convex Hull, cost trade off, etc