Quasi-bialgebra
Encyclopedia
In mathematics
, quasi-bialgebras are a generalization of bialgebra
s, which were defined by the Ukrainian
mathematician Vladimir Drinfel'd
in 1990.
A quasi-bialgebra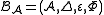
is an algebra
over a field
of characteristic
zero equipped with morphisms of algebras
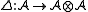
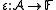
and an invertible element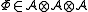
such that the following are true
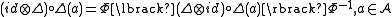
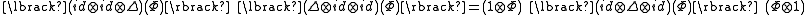
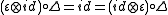
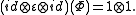
The main difference between bialgebra
s and quasi-bialgebras is that for the latter comultiplication is no longer coassociative.
If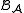
is a quasi-bialgebra and 
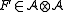is an invertible element such that 
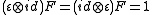, set
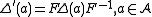
Then, the set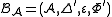
is also a quasi-bialgebra obtained by twisting 
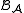by F, which is called a twist. Twisting by 
and then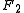 
is equivalent to twisting by 
.
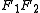of quantum affine algebra. F-matrices can be used to factorize the corresponding R-matrix
.This leads to applications in statistical mechanics
, as quantum affine algebras, and their representations give rise to solutions of the Yang-Baxter equation
, a solvability condition for various statistical models, allowing characteristics of the model to be deduced from its corresponding quantum affine algebra. The study of F-matrices has been applied to models such as the Heisenberg XXZ model in the framework of the Algebraic Bethe ansatz
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, quasi-bialgebras are a generalization of bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
s, which were defined by the Ukrainian
Ukraine
Ukraine is a country in Eastern Europe. It has an area of 603,628 km², making it the second largest contiguous country on the European continent, after Russia...
mathematician Vladimir Drinfel'd
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
in 1990.
A quasi-bialgebra
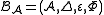is an algebraAlgebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
zero equipped with morphisms of algebras
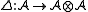
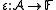
and an invertible element
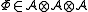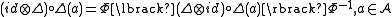
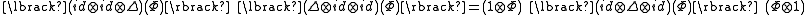
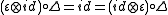
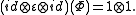
such that the following are trueThe main difference between bialgebra
Bialgebra
In mathematics, a bialgebra over a field K is a vector space over K which is both a unital associative algebra and a coalgebra, such that these structures are compatible....
s and quasi-bialgebras is that for the latter comultiplication is no longer coassociative.
Twisting
Given a quasi-bialgebra, further quasi-bialgebras can be generated by twisting.If
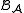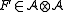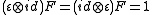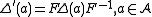
is a quasi-bialgebra and is an invertible element such that , setThen, the set
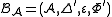is also a quasi-bialgebra obtained by twisting 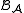by F, which is called a twist. Twisting by and then 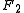is equivalent to twisting by 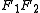.Usage
Quasi-bialgebras form the basis of the study of quasi-Hopf algebras and further to the study of Drinfeld twists and the representations in terms of F-matrices associated with finite-dimensional irreducible representationsRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of quantum affine algebra. F-matrices can be used to factorize the corresponding R-matrix
R-matrix
The term R-matrix has several meanings, depending on the field of study.The term R-matrix is used in connection with the Yang–Baxter equation. This is an equation which was first introduced in the field of statistical mechanics, taking its name from independent work of C. N. Yang and R. J....
.This leads to applications in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, as quantum affine algebras, and their representations give rise to solutions of the Yang-Baxter equation
Yang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
, a solvability condition for various statistical models, allowing characteristics of the model to be deduced from its corresponding quantum affine algebra. The study of F-matrices has been applied to models such as the Heisenberg XXZ model in the framework of the Algebraic Bethe ansatz
Bethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
.