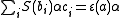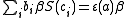Quasi-Hopf algebra
Encyclopedia
A quasi-Hopf algebra is a generalization of a Hopf algebra
, which was defined by the Russia
n mathematician Vladimir Drinfeld in 1989.
A quasi-Hopf algebra is a quasi-bialgebra
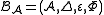 for which there exist
for which there exist 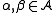 and a bijective
and a bijective
antihomomorphism
S (antipode
) of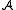 such that
such that
for all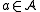 and where
and where

and
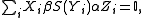
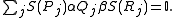
where the expansions for the quantities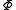 and
and 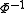 are given by
are given by
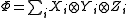
and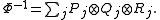
As for a quasi-bialgebra
, the property of being quasi-Hopf is preserved under twisting.
of quantum affine algebra. F-matrices can be used to factorize the corresponding R-matrix
. This leads to applications in Statistical mechanics
, as quantum affine algebras, and their representations give rise to solutions of the Yang-Baxter equation
, a solvability condition for various statistical models, allowing characteristics of the model to be deduced from its corresponding quantum affine algebra. The study of F-matrices has been applied to models such as the Heisenberg XXZ model in the framework of the algebraic Bethe ansatz
. It provides a framework for solving two-dimensional integrable models by using the Quantum inverse scattering method
.
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
, which was defined by the Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician Vladimir Drinfeld in 1989.
A quasi-Hopf algebra is a quasi-bialgebra
Quasi-bialgebra
In mathematics, quasi-bialgebras are a generalization of bialgebras, which were defined by the Ukrainian mathematician Vladimir Drinfel'd in 1990....
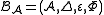 for which there exist
for which there exist 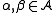 and a bijective
and a bijectiveBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
antihomomorphism
Antihomomorphism
In mathematics, an antihomomorphism is a type of function defined on sets with multiplication that reverses the order of multiplication. An antiautomorphism is an antihomomorphism which has an inverse as an antihomomorphism; this coincides with it being a bijection from an object to...
S (antipode
Antipode
Antipode, Antipodes, or Antipodeans may refer to:* Antipodal point, the diametrically opposite point on a sphere* Antipodes Water Company, a premium bottled water brand...
) of
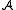 such that
such thatfor all
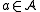 and where
and where
and
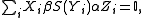
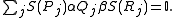
where the expansions for the quantities
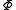 and
and 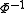 are given by
are given by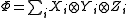
and
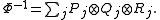
As for a quasi-bialgebra
Quasi-bialgebra
In mathematics, quasi-bialgebras are a generalization of bialgebras, which were defined by the Ukrainian mathematician Vladimir Drinfel'd in 1990....
, the property of being quasi-Hopf is preserved under twisting.
Usage
Quasi-Hopf algebras form the basis of the study of Drinfeld twists and the representations in terms of F-matrices associated with finite-dimensional irreducible representationsRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of quantum affine algebra. F-matrices can be used to factorize the corresponding R-matrix
R-matrix
The term R-matrix has several meanings, depending on the field of study.The term R-matrix is used in connection with the Yang–Baxter equation. This is an equation which was first introduced in the field of statistical mechanics, taking its name from independent work of C. N. Yang and R. J....
. This leads to applications in Statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, as quantum affine algebras, and their representations give rise to solutions of the Yang-Baxter equation
Yang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
, a solvability condition for various statistical models, allowing characteristics of the model to be deduced from its corresponding quantum affine algebra. The study of F-matrices has been applied to models such as the Heisenberg XXZ model in the framework of the algebraic Bethe ansatz
Bethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
. It provides a framework for solving two-dimensional integrable models by using the Quantum inverse scattering method
Quantum inverse scattering method
Quantum inverse scattering method relates two different approaches:1) Inverse scattering transform is a method of solving classical integrable differential equations of evolutionary type.Important concept is Lax representation....
.
See also
- Quasitriangular Hopf algebra
- Quasi-triangular Quasi-Hopf algebraQuasi-triangular Quasi-Hopf algebraA quasi-triangular quasi-Hopf algebra is a specialized form of a quasi-Hopf algebra defined by the Ukrainian mathematician Vladimir Drinfeld in 1989...
- Ribbon Hopf algebraRibbon Hopf algebraA ribbon Hopf algebra is a quasitriangular Hopf algebra which possess an invertible central element \nu more commonly known as the ribbon element, such that the following conditions hold:...