Active set
Encyclopedia
In optimization
, a problem is defined using an objective function to minimize or maximize, and a set of constraints
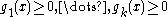
that define the feasible region, that is, the set of all x to search for the optimal solution. Given a point
in the feasible region, a constraint
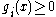
is called active at
if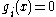 
and inactive at 
if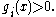 
Equality constraints are always active. The active set at 
is made up of those constraints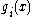 
that are active at the current point .
The active set is particularly important in optimization theory as it determines which constraints will influence the final result of optimization. For example, in solving the linear programming
problem, the active set gives the hyperplanes that intersect at the solution point. In quadratic programming
, as the solution is not mandatorily on one of the edges of the bounding polygon, an estimation of the active set gives us a subset of inequalities to watch while searching the solution, which reduces the complexity of the search.
In general an active set algorithm has the following structure:
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, a problem is defined using an objective function to minimize or maximize, and a set of constraints
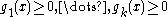
that define the feasible region, that is, the set of all x to search for the optimal solution. Given a point
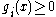
in the feasible region, a constraintis called active at
if 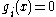and inactive at if 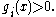Equality constraints are always active. The active set at is made up of those constraints 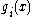that are active at the current point .The active set is particularly important in optimization theory as it determines which constraints will influence the final result of optimization. For example, in solving the linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problem, the active set gives the hyperplanes that intersect at the solution point. In quadratic programming
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
, as the solution is not mandatorily on one of the edges of the bounding polygon, an estimation of the active set gives us a subset of inequalities to watch while searching the solution, which reduces the complexity of the search.
In general an active set algorithm has the following structure:
- Find a feasible starting point
- repeat until "optimal enough"
- solve the equality problem defined by the active set (approximately)
- compute the Lagrange multipliersLagrange multipliersIn mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
of the active set - remove a subset of the constraints with negative Lagrange multipliers
- search for infeasible constraints
- end repeat