
Quadratically constrained quadratic program
Encyclopedia
In mathematics, a quadratically constrained quadratic program (QCQP) is an optimization problem in which both the objective function and the constraints are quadratic functions. It has the form
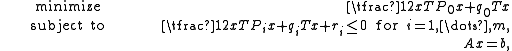
where P0, … Pm are n-by-n matrices and x ∈ Rn is the optimization variable.
If P0, … Pm are all positive semidefinite
, then the problem is convex
. If these matrices are neither positive or negative semidefinite, the problem is non-convex. If these are all zero, then the constraints are in fact linear and the problem is a quadratic program.
problem. To see this, note that the two constraints x1(x1 − 1) ≤ 0 and x1(x1 − 1) ≥ 0 are equivalent to the constraint x1(x1 − 1) = 0, which is in turn equivalent to the constraint x1 ∈ {0, 1}. Hence, any 0–1 integer program (in which all variables have to be either 0 or 1) can be formulated as a quadratically constrained quadratic program. Since 0–1 integer programming is NP-hard in general, QCQP is also NP-hard.
(SDP), and using the reformulation-linearization technique (RLT).
, the problem is convex and can be readily solved using interior point method
s, as done with semidefinite programming
.
is a problem in graph theory, which is NP-hard. Given a graph, the problem is to divide the vertices in two sets, so that as many edges as possible go from one set to the other. Max Cut can be formulated as a QCQP, and SDP relaxation of the dual provides good lower bounds.
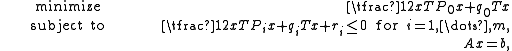
where P0, … Pm are n-by-n matrices and x ∈ Rn is the optimization variable.
If P0, … Pm are all positive semidefinite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, then the problem is convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
. If these matrices are neither positive or negative semidefinite, the problem is non-convex. If these are all zero, then the constraints are in fact linear and the problem is a quadratic program.
Hardness
Solving the general case is an NP-hardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
problem. To see this, note that the two constraints x1(x1 − 1) ≤ 0 and x1(x1 − 1) ≥ 0 are equivalent to the constraint x1(x1 − 1) = 0, which is in turn equivalent to the constraint x1 ∈ {0, 1}. Hence, any 0–1 integer program (in which all variables have to be either 0 or 1) can be formulated as a quadratically constrained quadratic program. Since 0–1 integer programming is NP-hard in general, QCQP is also NP-hard.
Relaxation
There are two main relaxations of QCQP: using semidefinite programmingSemidefinite programming
Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....
(SDP), and using the reformulation-linearization technique (RLT).
Semidefinite programming
When P0, … Pm are all positive-definite matricesPositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, the problem is convex and can be readily solved using interior point method
Interior point method
Interior point methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems.The interior point method was invented by John von Neumann...
s, as done with semidefinite programming
Semidefinite programming
Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective functionover the intersection of the cone of positive semidefinite matrices with an affine space, i.e., a spectrahedron....
.
Example
Max CutCut (graph theory)
In graph theory, a cut is a partition of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the set of edges whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set.In an unweighted undirected graph, the...
is a problem in graph theory, which is NP-hard. Given a graph, the problem is to divide the vertices in two sets, so that as many edges as possible go from one set to the other. Max Cut can be formulated as a QCQP, and SDP relaxation of the dual provides good lower bounds.

