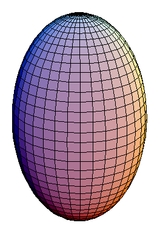
Prolate spheroid - AbsoluteAstronomy.com

A prolate spheroid is a spheroid

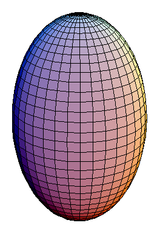
Spheroid

A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....

in which the polar axis is greater than the equator

Equator

An equator is the intersection of a sphere's surface with the plane perpendicular to the sphere's axis of rotation and containing the sphere's center of mass....

ial diameter. Prolate spheroids stand in contrast to oblate spheroids. The prolate spheroid is defined by the equation

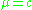for some arbitrary constant c, in prolate spheroidal coordinates

Prolate spheroidal coordinates

Prolate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating a spheroid around its major axis, i.e., the axis on which the foci are located...

Properties

A prolate spheroid has the surface area

Surface area

Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...

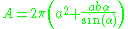
where

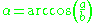is the angular eccentricity

Angular eccentricity

In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity....

of the ellipse,

is its (ordinary) eccentricity

Eccentricity (mathematics)

In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...

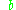is the polar radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

, and

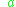is the equatorial radius.

The volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

of a prolate spheroid is calculated by

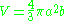
Uses

The prolate spheroid is the shape of the ball in several sports, such as in Rugby union

Rugby union

Rugby union, often simply referred to as rugby, is a full contact team sport which originated in England in the early 19th century. One of the two codes of rugby football, it is based on running with the ball in hand...

, Rugby league

Rugby league

Rugby league football, usually called rugby league, is a full contact sport played by two teams of thirteen players on a rectangular grass field. One of the two codes of rugby football, it originated in England in 1895 by a split from Rugby Football Union over paying players...

, and Australian rules football

Australian rules football

Australian rules football, officially known as Australian football, also called football, Aussie rules or footy is a sport played between two teams of 22 players on either...

. In American football

American football

American football is a sport played between two teams of eleven with the objective of scoring points by advancing the ball into the opposing team's end zone. Known in the United States simply as football, it may also be referred to informally as gridiron football. The ball can be advanced by...

and Canadian football

Canadian football

Canadian football is a form of gridiron football played exclusively in Canada in which two teams of 12 players each compete for territorial control of a field of play long and wide attempting to advance a pointed prolate spheroid ball into the opposing team's scoring area...

, a more pointed prolate spheroid is used (one resembling a vesica piscis

Vesica piscis

The vesica piscis is a shape that is the intersection of two circles with the same radius, intersecting in such a way that the center of each circle lies on the circumference of the other. The name literally means the "bladder of a fish" in Latin...

in cross section).

Several moons of the Solar system approximate prolate spheroids in shape, though they are actually scalene. Examples are Mimas

Mimas (moon)

Mimas is a moon of Saturn which was discovered in 1789 by William Herschel. It is named after Mimas, a son of Gaia in Greek mythology, and is also designated Saturn I....

, Enceladus

Enceladus (moon)

Enceladus is the sixth-largest of the moons of Saturn. It was discovered in 1789 by William Herschel. Until the two Voyager spacecraft passed near it in the early 1980s very little was known about this small moon besides the identification of water ice on its surface...

, and Tethys

Tethys (moon)

Tethys or Saturn III is a mid-sized moon of Saturn about across. It was discovered by G. D. Cassini in 1684 and is named after titan Tethys of Greek mythology. Tethys is pronounced |Odysseus]] is about 400 km in diameter, while the largest graben—Ithaca Chasma is about 100 km wide and...

(satellites of Saturn

Saturn

Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...

) and Miranda

Miranda (moon)

-External links:* at * at The Nine8 Planets* at Views of the Solar System* * from the...

(a satellite of Uranus

Uranus

Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus...

). In contrast to being distorted into oblate spheroids via rapid rotation, celestial objects distort slightly into prolate spheroids via tidal forces

Tide

Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the moon and the sun and the rotation of the Earth....

when they orbit a massive body in a close orbit. The most extreme example is Jupiter's moon Io

Io (moon)

Io ) is the innermost of the four Galilean moons of the planet Jupiter and, with a diameter of , the fourth-largest moon in the Solar System. It was named after the mythological character of Io, a priestess of Hera who became one of the lovers of Zeus....

, which becomes slightly more or less prolate in its orbit due to a slight eccentricity, causing spectacular volcanism

Volcanism

Volcanism is the phenomenon connected with volcanoes and volcanic activity. It includes all phenomena resulting from and causing magma within the crust or mantle of a planet to rise through the crust and form volcanic rocks on the surface....

. It should be noted that the axis of the prolate spheroid does not run through the satellite's poles in this case, but through the two points on its equator directly facing toward and away from the primary.

It is also used to describe the shape of some nebulae (nebulas) such as the Crab Nebula

Crab Nebula

The Crab Nebula is a supernova remnant and pulsar wind nebula in the constellation of Taurus...

.

The most common shapes for the density distribution of protons and neutrons in an atomic nucleus

Atomic nucleus

The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...

are spherical, prolate and oblate spheroidal. Deformed shapes occur as a result of the competition between electromagnetic repulsion between protons, surface tension

Surface tension

Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...

and quantum

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

shell effects.

Properties

Uses

See also