
Prolate spheroidal coordinates
Encyclopedia
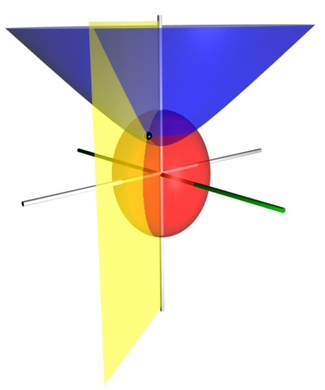
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
that results from rotating a spheroid around its major axis, i.e., the axis on which the foci are located. Rotation about the other axis produces the oblate spheroidal coordinates
Oblate spheroidal coordinates
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of...
.
Prolate spheroidal coordinates can be used to solve various partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s in which the boundary conditions match its symmetry and shape, such as solving for a field produced by two centers, which are taken as the foci on the z-axis. One example is solving for the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
moving in the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
of two positively charged nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
, as in the hydrogen molecular ion
Hydrogen molecular ion
The hydrogen molecular ion, dihydrogen cation, or H2+, is the simplest molecular ion. It is composed of two positively-charged protons and one negatively-charged electron, and can be formed from ionization of a neutral hydrogen molecule...
, H2+. Another example is solving for the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
generated by two small electrode
Electrode
An electrode is an electrical conductor used to make contact with a nonmetallic part of a circuit...
tips. Other limiting cases include areas generated by a line segment (μ=0) or a line with a missing segment (ν=0).
Definition

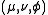 is
is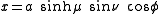
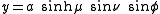
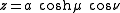
where
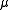 is a nonnegative real number and
is a nonnegative real number and 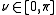 . The azimuthal angle
. The azimuthal angle 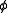 belongs to the interval
belongs to the interval 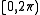 .
.The trigonometric identity
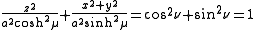
shows that surfaces of constant
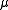 form prolate spheroids, since they are ellipse
form prolate spheroids, since they are ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s rotated about the axis
joining their foci. Similarly, the hyperbolic trigonometric identity
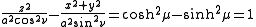
shows that surfaces of constant
 form
formhyperboloids of revolution.
Scale factors
The scale factors for the elliptic coordinates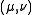 are equal
are equal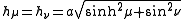
whereas the azimuthal scale factor equals
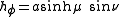
Consequently, an infinitesimal volume element equals
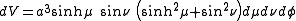
and the Laplacian can be written
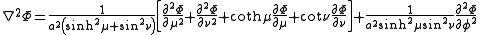
Other differential operators such as
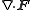 and
and  can be expressed in the coordinates
can be expressed in the coordinates 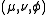 by substituting the scale factors into the general formulae found in orthogonal coordinates
by substituting the scale factors into the general formulae found in orthogonal coordinatesOrthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Alternative definition
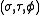 are sometimes used,
are sometimes used,where
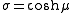 and
and 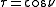 . Hence, the curves of constant
. Hence, the curves of constant  are prolate spheroids, whereas the curves of constant
are prolate spheroids, whereas the curves of constant  are hyperboloids of revolution. The coordinate
are hyperboloids of revolution. The coordinate  belongs to the interval [-1, 1], whereas the
belongs to the interval [-1, 1], whereas the  coordinate must be greater than or equal to one.
coordinate must be greater than or equal to one.The coordinates
 and
and  have a simple relation to the distances to the foci
have a simple relation to the distances to the foci 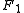 and
and 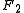 . For any point in the plane, the sum
. For any point in the plane, the sum 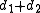 of its distances to the foci equals
of its distances to the foci equals 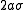 , whereas their difference
, whereas their difference 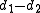 equals
equals 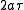 . Thus, the distance to
. Thus, the distance to 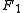 is
is 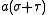 , whereas the distance to
, whereas the distance to 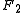 is
is 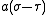 . (Recall that
. (Recall that 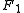 and
and 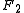 are located at
are located at 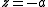 and
and 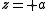 , respectively.)
, respectively.)Unlike the analogous oblate spheroidal coordinates
Oblate spheroidal coordinates
Oblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of...
, the prolate spheroid coordinates (σ, τ, φ) are not degenerate; in other words, there is a unique, reversible correspondence between them and the Cartesian coordinates

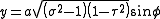
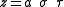
Alternative scale factors
The scale factors for the alternative elliptic coordinates are
are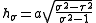

while the azimuthal scale factor is now
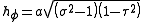
Hence, the infinitesimal volume element becomes
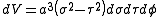
and the Laplacian equals
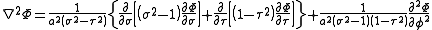
Other differential operators such as
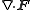 and
and 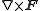 can be expressed in the coordinates
can be expressed in the coordinates  by substituting the scale factors into the general formulae found in orthogonal coordinates
by substituting the scale factors into the general formulae found in orthogonal coordinatesOrthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
As is the case with spherical coordinates, Laplace's equation may be solved by the method of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
to yield solutions in the form of prolate spheroidal harmonics, which are convenient to use when boundary conditions are defined on a surface with a constant prolate spheroidal coordinate (See Smythe, 1968).
No angles convention
Uses ξ1 = a cosh μ, ξ2 = sin ν, and ξ3 = cos φ. Same as Morse & Feshbach (1953), substituting uk for ξk. | page = 97}} Uses coordinates ξ = cosh μ, η = sin ν, and φ.Angle convention
| page = 177}} Korn and Korn use the (μ, ν, φ) coordinates, but also introduce the degenerate (σ, τ, φ) coordinates.| pages = 180–182 }} Similar to Korn and Korn (1961), but uses colatitudeColatitude
In spherical coordinates, colatitude is the complementary angle of the latitude, i.e. the difference between 90° and the latitude.-Astronomical use:The colatitude is useful in astronomy because it refers to the zenith distance of the celestial poles...
θ = 90° - ν instead of latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
ν. Moon and Spencer use the colatitude convention θ = 90° - ν, and re-name φ as ψ.
Unusual convention
Treats the prolate spheroidal coordinates as a limiting case of the general ellipsoidal coordinatesEllipsoidal coordinates
Ellipsoidal coordinates are a three-dimensional orthogonal coordinate system that generalizes the two-dimensional elliptic coordinate system...
. Uses (ξ, η, ζ) coordinates that have the units of distance squared.

