Priestley space
Encyclopedia
In mathematics
, a Priestley space is an ordered topological space
with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them. Priestley spaces play a fundamental role in the study of distributive lattice
s. In particular, there is a duality
between the category
of Priestley spaces and the category of bounded distributive lattices.
the following two conditions:
(i) is compact
.
(ii) If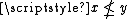
, then there exists a clopen
up-set of such that and . (This condition is known as the Priestley separation axiom.)
It follows that for each Priestley space , the topological space is a Stone space; that is, it is a compact Hausdorff zero-dimensional space.
Some further useful properties of Priestley spaces are listed below.
Let be a Priestley space.
A Priestley morphism from a Priestley space to another Priestley space is a map which is continuous and order-preserving.
Let Pries denote the category of Priestley spaces and Priestley morphisms.
s. For a Priestley space , let denote the collection of all open up-sets of . Similarly, let denote the collection of all open down-sets of .
Theorem: If is a Priestley space, then both and are spectral spaces.
Conversely, given a spectral space , let denote the patch topology on ; that is, the topology generated by the subbasis consisting of compact open subsets of and their complement
s. Let also denote the specialization order of .
Theorem: If is a spectral space, then is a Priestley space.
In fact, this correspondence between Priestley spaces and spectral spaces is functorial and yields an isomorphism
between Pries and the category Spec of spectral spaces and spectral map
s.
s.
Theorem: If is a Priestley space, then is a pairwise Stone space
. Conversely, if is a pairwise Stone space, then is a Priestley space, where is the join of and and is the specialization order of .
The correspondence between Priestley spaces and pairwise Stone spaces is functorial and yields an isomorphism between the category Pries of Priestley spaces and Priestley morphisms and the category PStone of pairwise Stone spaces and bi-continuous maps.
Thus, one has the following isomorphisms of categories:
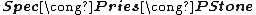
One of the main consequences of the duality theory for distributive lattices
is that each of these categories is dually equivalent to the category of bounded distributive lattice
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Priestley space is an ordered topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them. Priestley spaces play a fundamental role in the study of distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
s. In particular, there is a duality
Duality theory for distributive lattices
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces...
between the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of Priestley spaces and the category of bounded distributive lattices.
Definition
A Priestley space is an ordered topological space , i. e. a set equipped with a partial order and a topology , satisfyingthe following two conditions:
(i) is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
(ii) If
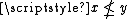, then there exists a clopenClopen set
In topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
up-set of such that and . (This condition is known as the Priestley separation axiom.)
Properties of Priestley spaces
- Each Priestley space is HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. Indeed, given two points of a Priestley space , if , then as is a partial order, either
or 
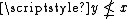. Assuming, without loss of generality, that 
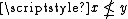, (ii) provides a clopen up-set of such that and . Therefore, and are disjoint open subsets of separating and .
- Each Priestley space is also zero-dimensional; that is, each open neighborhood of a point of a Priestley space contains a clopen neighborhood of . To see this, one proceeds as follows. For each , either
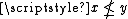or 
. By the Priestley separation axiom, there exists a clopen up-set or a clopen down-set containing and missing . Obviously the intersection of these clopen neighborhoods of does not meet . Therefore, as is compact, there exists a finite intersection of these clopen neighborhoods of missing . This finite intersection is the desired clopen neighborhood of contained in .
It follows that for each Priestley space , the topological space is a Stone space; that is, it is a compact Hausdorff zero-dimensional space.
Some further useful properties of Priestley spaces are listed below.
Let be a Priestley space.
-
- (a) For each closed subset of , both and are closed subsets of .
-
- (b) Each open up-set of is a union of clopen up-sets of and each open down-set of is a union of clopen down-sets of .
-
- (c) Each closed up-set of is an intersection of clopen up-sets of and each closed down-set of is an intersection of clopen down-sets of .
-
- (d) Clopen up-sets and clopen down-sets of form a subbasis for .
-
- (e) For each pair of closed subsets and of , if , then there exists a clopen up-set such that and .
A Priestley morphism from a Priestley space to another Priestley space is a map which is continuous and order-preserving.
Let Pries denote the category of Priestley spaces and Priestley morphisms.
Connection with spectral spaces
Priestley spaces are closely related to spectral spaceSpectral space
In mathematics, a spectral space is a topological space which is homeomorphic to the spectrum of a commutative ring.-Definition:Let X be a topological space and let K\circ be the set of allquasi-compact and open subsets of X...
s. For a Priestley space , let denote the collection of all open up-sets of . Similarly, let denote the collection of all open down-sets of .
Theorem: If is a Priestley space, then both and are spectral spaces.
Conversely, given a spectral space , let denote the patch topology on ; that is, the topology generated by the subbasis consisting of compact open subsets of and their complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
s. Let also denote the specialization order of .
Theorem: If is a spectral space, then is a Priestley space.
In fact, this correspondence between Priestley spaces and spectral spaces is functorial and yields an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
between Pries and the category Spec of spectral spaces and spectral map
Spectral space
In mathematics, a spectral space is a topological space which is homeomorphic to the spectrum of a commutative ring.-Definition:Let X be a topological space and let K\circ be the set of allquasi-compact and open subsets of X...
s.
Connection with bitopological spaces
Priestley spaces are also closely related to bitopological spaceBitopological space
In mathematics, a bitopological space is a set endowed with two topologies. Typically, if the set is X and the topologies are \sigma and \tau then we refer to the bitopological space as .-Bi-continuity:...
s.
Theorem: If is a Priestley space, then is a pairwise Stone space
Pairwise Stone space
In mathematics and particularly in topology, pairwise Stone space is a bitopological space \scriptstyle which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional....
. Conversely, if is a pairwise Stone space, then is a Priestley space, where is the join of and and is the specialization order of .
The correspondence between Priestley spaces and pairwise Stone spaces is functorial and yields an isomorphism between the category Pries of Priestley spaces and Priestley morphisms and the category PStone of pairwise Stone spaces and bi-continuous maps.
Thus, one has the following isomorphisms of categories:
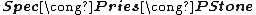
One of the main consequences of the duality theory for distributive lattices
Duality theory for distributive lattices
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces...
is that each of these categories is dually equivalent to the category of bounded distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
s.
See also
- Spectral spaceSpectral spaceIn mathematics, a spectral space is a topological space which is homeomorphic to the spectrum of a commutative ring.-Definition:Let X be a topological space and let K\circ be the set of allquasi-compact and open subsets of X...
- Pairwise Stone spacePairwise Stone spaceIn mathematics and particularly in topology, pairwise Stone space is a bitopological space \scriptstyle which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional....
- Distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
- Stone dualityStone dualityIn mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
- Duality theory for distributive latticesDuality theory for distributive latticesIn mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces...