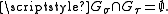Bitopological space
Encyclopedia
In mathematics
, a bitopological space is a set endowed with two topologies
. Typically, if the set is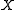 and the topologies are
and the topologies are  and
and  then we refer to the bitopological space as
then we refer to the bitopological space as 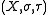 .
.
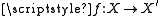 from a bitopological space
from a bitopological space 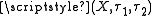 to another bitopological space
to another bitopological space 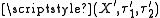 is called bi-continuous if
is called bi-continuous if 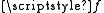 is continuous both as a map from
is continuous both as a map from 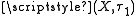 to
to 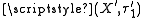 and as map from
and as map from 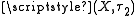 to
to 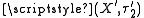 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bitopological space is a set endowed with two topologies
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. Typically, if the set is
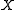 and the topologies are
and the topologies are  and
and  then we refer to the bitopological space as
then we refer to the bitopological space as 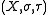 .
.Bi-continuity
A mapMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
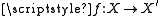 from a bitopological space
from a bitopological space 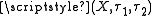 to another bitopological space
to another bitopological space 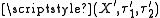 is called bi-continuous if
is called bi-continuous if 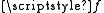 is continuous both as a map from
is continuous both as a map from 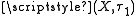 to
to 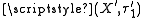 and as map from
and as map from 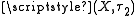 to
to 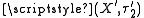 .
.Bitopological variants of topological properties
Corresponding to well-known properties of topological spaces, there are versions for bitopological spaces.- A bitopological space
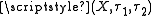 is pairwise compact if each cover
is pairwise compact if each cover 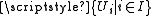 of
of 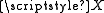 with
with 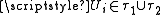 , contains a finite subcover.
, contains a finite subcover.
- A bitopological space
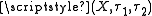 is pairwise Hausdorff if for any two distinct points
is pairwise Hausdorff if for any two distinct points 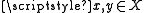 there exist disjoint
there exist disjoint 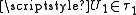 and
and  with either
with either 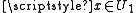 and
and  or
or 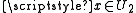 and
and 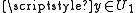 .
.
- A bitopological space
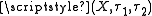 is pairwise zero-dimensional if opens in
is pairwise zero-dimensional if opens in 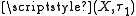 which are closed in
which are closed in 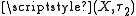 form a basis for
form a basis for 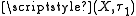 , and opens in
, and opens in 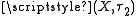 which are closed in
which are closed in  form a basis for
form a basis for 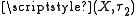 .
.
- A bitopological space
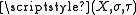 is called binormal if for every
is called binormal if for every 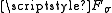
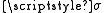 -closed and
-closed and 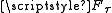
 -closed sets there are
-closed sets there are 
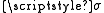 -open and
-open and 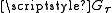
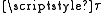 -open sets such that
-open sets such that 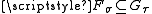
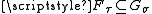 , and
, and