
Pairwise Stone space
Encyclopedia
In mathematics
and particularly in topology
, pairwise Stone space is a bitopological space
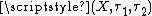 which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional.
which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional.
Pairwise Stone spaces are a bitopological version of the Stone spaces.
Pairwise Stone spaces are closely related to spectral space
s.
Theorem: If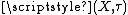 is a spectral space, then
is a spectral space, then 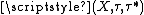 is a pairwise Stone space, where
is a pairwise Stone space, where 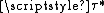 is the de Groot dual
is the de Groot dual
topology of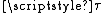 . Conversely, if
. Conversely, if 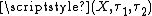 is a pairwise Stone space, then both
is a pairwise Stone space, then both 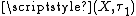 and
and 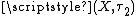 are spectral spaces.
are spectral spaces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and particularly in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, pairwise Stone space is a bitopological space
Bitopological space
In mathematics, a bitopological space is a set endowed with two topologies. Typically, if the set is X and the topologies are \sigma and \tau then we refer to the bitopological space as .-Bi-continuity:...
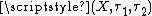 which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional.
which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional.Pairwise Stone spaces are a bitopological version of the Stone spaces.
Pairwise Stone spaces are closely related to spectral space
Spectral space
In mathematics, a spectral space is a topological space which is homeomorphic to the spectrum of a commutative ring.-Definition:Let X be a topological space and let K\circ be the set of allquasi-compact and open subsets of X...
s.
Theorem: If
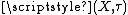 is a spectral space, then
is a spectral space, then 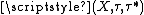 is a pairwise Stone space, where
is a pairwise Stone space, where 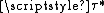 is the de Groot dual
is the de Groot dualDe Groot dual
In mathematics, in particular in topology, the de Groot dual of a topology τ on a set X is the topology τ* whose closed sets are generated by compact saturated subsets of .- References :...
topology of
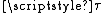 . Conversely, if
. Conversely, if 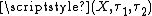 is a pairwise Stone space, then both
is a pairwise Stone space, then both 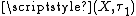 and
and 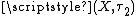 are spectral spaces.
are spectral spaces.

