Extrapolation
Encyclopedia
In mathematics
, extrapolation is the process of constructing new data points. It is similar to the process of interpolation
, which constructs new points between known points, but the results of extrapolations are often less meaningful, and are subject to greater uncertainty
. It may also mean extension of a method, assuming similar methods will be applicable. Extrapolation may also apply to human experience
to project, extend, or expand known experience into an area not known or previously experienced so as to arrive at a (usually conjectural) knowledge of the unknown (e.g. a driver extrapolates road conditions beyond his sight while driving).
If the two data points nearest the point to be extrapolated are
to be extrapolated are  and
and  , linear extrapolation gives the function:
, linear extrapolation gives the function:

(which is identical to linear interpolation
if ). It is possible to include more than two points, and averaging the slope of the linear interpolant, by regression
). It is possible to include more than two points, and averaging the slope of the linear interpolant, by regression
-like techniques, on the data points chosen to be included. This is similar to linear prediction
.
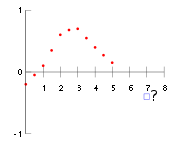
High-order polynomial extrapolation must be used with due care. For the example data set and problem in the figure above, anything above order 1 (linear extrapolation) will possibly yield unusable values, an error estimate of the extrapolated value will grow with the degree of the polynomial extrapolation. This is related to Runge's phenomenon
.
will be poorly extrapolated.
Even for proper assumptions about the function, the extrapolation can diverge strongly from the function. The classic example is truncated power series representations of sin(x) and related trigonometric function
s. For instance, taking only data from near the x = 0, we may estimate that the function behaves as sin(x) ~ x. In the neighborhood of x = 0, this is an excellent estimate. Away from x = 0 however, the extrapolation moves arbitrarily away from the x-axis while sin(x) remains in the interval
[−1,1]. I.e., the error increases without bound.
Taking more terms in the power series of sin(x) around x = 0 will produce better agreement over a larger interval near x = 0, but will produce extrapolations that eventually diverge away from the x-axis even faster than the linear approximation.
This divergence is a specific property of extrapolation methods and is only circumvented when the functional forms assumed by the extrapolation method (inadvertently or intentionally due to additional information) accurately represent the nature of the function being extrapolated. For particular problems, this additional information may be available, but in the general case, it is impossible to satisfy all possible function behaviors with a workably small set of potential behavior
, a problem of extrapolation may be converted into an interpolation
problem by the change of variable . This transform exchanges the part of the complex plane
. This transform exchanges the part of the complex plane
inside the unit circle
with the part of the complex plane outside of the unit circle. In particular, the compactification
point at infinity is mapped to the origin and vice versa. Care must be taken with this transform however, since the original function may have had "features", for example poles and other singularities
, at infinity that were not evident from the sampled data.
Another problem of extrapolation is loosely related to the problem of analytic continuation
, where (typically) a power series representation of a function
is expanded at one of its points of convergence
to produce a power series with a larger radius of convergence
. In effect, a set of data from a small region is used to extrapolate a function onto a larger region.
Again, analytic continuation
can be thwarted by function
features that were not evident from the initial data.
Also, one may use sequence transformations like Padé approximant
s and Levin-type sequence transformations as extrapolation methods that lead to a summation
of power series that are divergent outside the original radius of convergence
. In this case, one often obtains
rational approximants.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, extrapolation is the process of constructing new data points. It is similar to the process of interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
, which constructs new points between known points, but the results of extrapolations are often less meaningful, and are subject to greater uncertainty
Uncertainty
Uncertainty is a term used in subtly different ways in a number of fields, including physics, philosophy, statistics, economics, finance, insurance, psychology, sociology, engineering, and information science...
. It may also mean extension of a method, assuming similar methods will be applicable. Extrapolation may also apply to human experience
Experience
Experience as a general concept comprises knowledge of or skill in or observation of some thing or some event gained through involvement in or exposure to that thing or event....
to project, extend, or expand known experience into an area not known or previously experienced so as to arrive at a (usually conjectural) knowledge of the unknown (e.g. a driver extrapolates road conditions beyond his sight while driving).

Extrapolation methods
A sound choice of which extrapolation method to apply relies on a prior knowledge of the process that created the existing data points. Crucial questions are for example if the data can be assumed to be continuous, smooth, possibly periodic etc.Linear extrapolation
Extrapolation means creating a tangent line at the end of the known data and extending it beyond as that limit. Linear extrapolation will only provide good results when used to extend the graph of an approximately linear function or not too far beyond the known data.If the two data points nearest the point
 to be extrapolated are
to be extrapolated are  and
and  , linear extrapolation gives the function:
, linear extrapolation gives the function:
(which is identical to linear interpolation
Linear interpolation
Linear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
if
 ). It is possible to include more than two points, and averaging the slope of the linear interpolant, by regression
). It is possible to include more than two points, and averaging the slope of the linear interpolant, by regressionRegression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
-like techniques, on the data points chosen to be included. This is similar to linear prediction
Linear prediction
Linear prediction is a mathematical operation where future values of a discrete-time signal are estimated as a linear function of previous samples....
.
Polynomial extrapolation
A polynomial curve can be created through the entire known data or just near the end. The resulting curve can then be extended beyond the end of the known data. Polynomial extrapolation is typically done by means of Lagrange interpolation or using Newton's method of finite differences to create a Newton series that fits the data. The resulting polynomial may be used to extrapolate the data.High-order polynomial extrapolation must be used with due care. For the example data set and problem in the figure above, anything above order 1 (linear extrapolation) will possibly yield unusable values, an error estimate of the extrapolated value will grow with the degree of the polynomial extrapolation. This is related to Runge's phenomenon
Runge's phenomenon
In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree...
.
Conic extrapolation
A conic section can be created using five points near the end of the known data. If the conic section created is an ellipse or circle, it will loop back and rejoin itself. A parabolic or hyperbolic curve will not rejoin itself, but may curve back relative to the X-axis. This type of extrapolation could be done with a conic sections template (on paper) or with a computer.French curve extrapolation
French curve extrapolation is a method suitable for any distribution that has a tendency to be exponential, but with accelerating or decelerating factors. This method has been used successfully in providing forecast projections of the growth of HIV/AIDS in the UK since 1987 and variant CJD in the UK for a number of years http://www.AIDSCJDUK.info.Quality of extrapolation
Typically, the quality of a particular method of extrapolation is limited by the assumptions about the function made by the method. If the method assumes the data are smooth, then a non-smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
will be poorly extrapolated.
Even for proper assumptions about the function, the extrapolation can diverge strongly from the function. The classic example is truncated power series representations of sin(x) and related trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s. For instance, taking only data from near the x = 0, we may estimate that the function behaves as sin(x) ~ x. In the neighborhood of x = 0, this is an excellent estimate. Away from x = 0 however, the extrapolation moves arbitrarily away from the x-axis while sin(x) remains in the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[−1,1]. I.e., the error increases without bound.
Taking more terms in the power series of sin(x) around x = 0 will produce better agreement over a larger interval near x = 0, but will produce extrapolations that eventually diverge away from the x-axis even faster than the linear approximation.
This divergence is a specific property of extrapolation methods and is only circumvented when the functional forms assumed by the extrapolation method (inadvertently or intentionally due to additional information) accurately represent the nature of the function being extrapolated. For particular problems, this additional information may be available, but in the general case, it is impossible to satisfy all possible function behaviors with a workably small set of potential behavior
Extrapolation in the complex plane
In complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a problem of extrapolation may be converted into an interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
problem by the change of variable
 . This transform exchanges the part of the complex plane
. This transform exchanges the part of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
inside the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
with the part of the complex plane outside of the unit circle. In particular, the compactification
Compactification
Compactification may refer to:* Compactification , making a topological space compact* Compactification , the "curling up" of extra dimensions in string theory* Compaction...
point at infinity is mapped to the origin and vice versa. Care must be taken with this transform however, since the original function may have had "features", for example poles and other singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
, at infinity that were not evident from the sampled data.
Another problem of extrapolation is loosely related to the problem of analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
, where (typically) a power series representation of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is expanded at one of its points of convergence
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
to produce a power series with a larger radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
. In effect, a set of data from a small region is used to extrapolate a function onto a larger region.
Again, analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
can be thwarted by function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
features that were not evident from the initial data.
Also, one may use sequence transformations like Padé approximant
Padé approximant
Padé approximant is the "best" approximation of a function by a rational function of given order - under this technique, the approximant's power series agrees with the power series of the function it is approximating....
s and Levin-type sequence transformations as extrapolation methods that lead to a summation
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
of power series that are divergent outside the original radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
. In this case, one often obtains
rational approximants.
See also
- ForecastingForecastingForecasting is the process of making statements about events whose actual outcomes have not yet been observed. A commonplace example might be estimation for some variable of interest at some specified future date. Prediction is a similar, but more general term...
- Minimum polynomial extrapolationMinimum polynomial extrapolationIn mathematics, minimum polynomial extrapolation is a sequence transformation used for convergence acceleration.While Aitken's method is the most famous, it often fails for vector sequences. An effective method for vector sequences is the minimum polynomial extrapolation...
- Multigrid methodMultigrid methodMultigrid methods in numerical analysis are a group of algorithms for solving differential equations using a hierarchy of discretizations. They are an example of a class of techniques called multiresolution methods, very useful in problems exhibiting multiple scales of behavior...
- Prediction intervalPrediction intervalIn statistical inference, specifically predictive inference, a prediction interval is an estimate of an interval in which future observations will fall, with a certain probability, given what has already been observed...
- Regression analysisRegression analysisIn statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
- Richardson extrapolationRichardson extrapolationIn numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....
- Static analysisStatic analysisStatic analysis, static projection, and static scoring are terms for simplified analysis wherein the effect of an immediate change to a system is calculated without respect to the longer term response of the system to that change...
- Trend estimationTrend estimationTrend estimation is a statistical technique to aid interpretation of data. When a series of measurements of a process are treated as a time series, trend estimation can be used to make and justify statements about tendencies in the data...
- InterpolationInterpolationIn the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
- Extrapolation domain analysisExtrapolation domain analysisExtrapolation domain analysis is a methodology for identifying geographical areas that seem suitable for adoption of innovative ecosystem management practices on the basis of sites exhibiting similarity in conditions such as climatic, land use and socio-economic indicators...
- Dead reckoningDead reckoningIn navigation, dead reckoning is the process of calculating one's current position by using a previously determined position, or fix, and advancing that position based upon known or estimated speeds over elapsed time, and course...

