
Tate module
Encyclopedia
In mathematics
, a Tate module of an abelian group, named for John Tate
, is a module
constructed from an abelian group
A. Often, this construction is made in the following situation: G is a commutative group scheme
over a field
K, Ks is the separable closure of K, and A = G(Ks) (the Ks-valued points of G
). In this case, the Tate module of A is equipped with an action
of the absolute Galois group
of K, and it is referred to as the Tate module of G.
p, the p-adic Tate module of A is
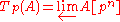
where A[pn] is the pn torsion
of A (i.e. the kernel
of the multiplication-by-pn map), and the inverse limit
is over positive integers n with transition morphisms given by the multiplication-by-p map A[pn+1] → A[pn]. Thus, the Tate module encodes all the p-power torsion of A. It is equipped with the structure of a Zp-module via

over Zp with a linear action of the absolute Galois group GK of K. Thus, it is a Galois representation also referred to as the p-adic cyclotomic character
of K. It can also be considered as the Tate module of the multiplicative group scheme
Gm,K over K.
G over a field K, the Ks-valued points of G are an abelian group. The p-adic Tate module Tp(G) of G is a Galois representation (of the absolute Galois group, GK, of K).
Classical results on abelian varieties show that if K has characteristic zero, or characteristic ℓ where the prime number p ≠ ℓ, then Tp(G) is a free module over Zp of rank 2d, where d is the dimension of G. In the other case, it is still free, but the rank may take any value from 0 to d (see for example Hasse–Witt matrix).
In the case where p is not equal to the characteristic of K, the p-adic Tate module of G is the dual
of the étale cohomology
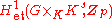 .
.
A special case of the Tate conjecture
can be phrased in terms of Tate modules. Suppose K is finitely generated
over its prime field (e.g. a finite field
, an algebraic number field
, a global function field), of characteristic different from p, and A and B are two abelian varieties over K. The Tate conjecture then predicts that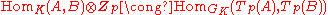
where HomK(A, B) is the group of morphisms of abelian varieties
from A to B, and the right-hand side is the group of GK-linear maps from Tp(A) to Tp(B). The case where K is a finite field was proved by Tate himself in the 1960s. Gerd Faltings
proved the case where K is a number field in his celebrated "Mordell paper".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Tate module of an abelian group, named for John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
, is a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
constructed from an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
A. Often, this construction is made in the following situation: G is a commutative group scheme
Group scheme
In mathematics, a group scheme is a type of algebro-geometric object equipped with a composition law. Group schemes arise naturally as symmetries of schemes, and they generalize algebraic groups, in the sense that all algebraic groups have group scheme structure, but group schemes are not...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, Ks is the separable closure of K, and A = G(Ks) (the Ks-valued points of G
Glossary of scheme theory
This is a glossary of scheme theory. For an introduction to the theory of schemes in algebraic geometry, see affine scheme, projective space, sheaf and scheme. The concern here is to list the fundamental technical definitions and properties of scheme theory...
). In this case, the Tate module of A is equipped with an action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the absolute Galois group
Absolute Galois group
In mathematics, the absolute Galois group GK of a field K is the Galois group of Ksep over K, where Ksep is a separable closure of K. Alternatively it is the group of all automorphisms of the algebraic closure of K that fix K. The absolute Galois group is unique up to isomorphism...
of K, and it is referred to as the Tate module of G.
Definition
Given an abelian group A and a prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p, the p-adic Tate module of A is
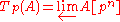
where A[pn] is the pn torsion
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
of A (i.e. the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the multiplication-by-pn map), and the inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
is over positive integers n with transition morphisms given by the multiplication-by-p map A[pn+1] → A[pn]. Thus, the Tate module encodes all the p-power torsion of A. It is equipped with the structure of a Zp-module via

The Tate module
When the abelian group A is the group of roots of unity in a separable closure Ks of K, the p-adic Tate module of A is sometimes referred to as the Tate module (where the choice of p and K are tacitly understood). It is a free rank one moduleFree module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
over Zp with a linear action of the absolute Galois group GK of K. Thus, it is a Galois representation also referred to as the p-adic cyclotomic character
Cyclotomic character
In number theory, a cyclotomic character is a character of a Galois group giving the Galois action on a group of roots of unity. As a one-dimensional representation over a ring R, its representation space is generally denoted by R .-p-adic cyclotomic character:If p is a prime, and G is the absolute...
of K. It can also be considered as the Tate module of the multiplicative group scheme
Algebraic torus
In mathematics, an algebraic torus is a type of commutative affine algebraic group. These groups were named by analogy with the theory of tori in Lie group theory...
Gm,K over K.
The Tate module of an abelian variety
Given an abelian varietyAbelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
G over a field K, the Ks-valued points of G are an abelian group. The p-adic Tate module Tp(G) of G is a Galois representation (of the absolute Galois group, GK, of K).
Classical results on abelian varieties show that if K has characteristic zero, or characteristic ℓ where the prime number p ≠ ℓ, then Tp(G) is a free module over Zp of rank 2d, where d is the dimension of G. In the other case, it is still free, but the rank may take any value from 0 to d (see for example Hasse–Witt matrix).
In the case where p is not equal to the characteristic of K, the p-adic Tate module of G is the dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
of the étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
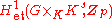 .
.A special case of the Tate conjecture
Tate conjecture
In mathematics, the Tate conjecture is a 1963 conjecture of John Tate linking algebraic geometry, and more specifically the identification of algebraic cycles, with Galois modules coming from étale cohomology...
can be phrased in terms of Tate modules. Suppose K is finitely generated
Finitely generated algebra
In mathematics, a finitely generated algebra is an associative algebra A over a field K where there exists a finite set of elements a1,…,an of A such that every element of A can be expressed as a polynomial in a1,…,an, with coefficients in K...
over its prime field (e.g. a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
, a global function field), of characteristic different from p, and A and B are two abelian varieties over K. The Tate conjecture then predicts that
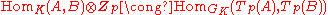
where HomK(A, B) is the group of morphisms of abelian varieties
Abelian variety
In mathematics, particularly in algebraic geometry, complex analysis and number theory, an abelian variety is a projective algebraic variety that is also an algebraic group, i.e., has a group law that can be defined by regular functions...
from A to B, and the right-hand side is the group of GK-linear maps from Tp(A) to Tp(B). The case where K is a finite field was proved by Tate himself in the 1960s. Gerd Faltings
Gerd Faltings
Gerd Faltings is a German mathematician known for his work in arithmetic algebraic geometry.From 1972 to 1978, he studied mathematics and physics at the University of Münster. In 1978 he received his PhD in mathematics and in 1981 he got the venia legendi in mathematics, both from the University...
proved the case where K is a number field in his celebrated "Mordell paper".

